Answers
The overall logarithmic function pertaining to f(x) exists within the stated domain of (0,1)U(1,infinity), whilst featuring a range of "all real numbers".
How to explain the functionA logarithmic function's domain is all positive real numbers except 0, as the logarithm of 0 is undefined. From our given table, we conclude that x values consist solely of positive powers of 5; this yields the following domain condition: x > 0 and x ≠ 1.
The range of a logarithmic function comprises every element in the set of real numbers. Despite observing y-values between -3 and 3 in our table, the potential for logarithmic functions to approach negative infinity when x approaches 0, long with the tendency to lean towards positive infinity as x approaches infinitely large values renders the range to encompass all real numbers.
Learn more about domain on
https://brainly.com/question/26098895
#SPJ1
Related Questions
I need help with these

Answers
The 15 and 9 units side lengths of the parallelogram ABCD, and the 36° measure of the acute interior angle, A indicates the values of the ratios are;
1. AB:BC = 5:3
2. AB:CD = 1:1
3. m∠A : m∠C= 1 : 4
4. m∠B:m∠C = 4:1
5. AD: Perimeter ABCD = 3:16
What is a ratio?A ratio is a representation of the number of times one quantity is contained in another quantity.
The shape of the quadrilateral ABCD in the question = A parallelogram
Length of AB = 15
Length of BC = 9
Measure of angle m∠A = 36°
Therefore;
1. AB:BC = 15:9 = 5:3
2. AB ≅ CD (Opposite sides of a parallelogram are congruent)
AB = CD (Definition of congruency)
AB = 15, therefore, CD = 15 transitive property
AB:CD = 15:15 = 1:1
3. ∠A ≅ ∠C (Opposite interior angles of a parallelogram are congruent)
Therefore; m∠A = m∠C = 36°
∠A and ∠D are supplementary angles (Same side interior angles formed between parallel lines)
Therefore; ∠A + ∠D = 180°
36° + ∠D = 180°
∠D = 180° - 36° = 144°
∠D = 144°
m∠A : m∠C = 36°:144° =1:4
m∠A : m∠C = 1:4
4. ∠B = ∠D = 144° (properties of a parallelogram)
m∠B : m∠C = 144° : 36° = 4:1
5. AD ≅ BC (opposite sides of a parallelogram)
AD = BC = 9 (definition of congruency)
The perimeter of the parallelogram ABCD = AB + BC + CD + DA
Therefore;
Perimeter of parallelogram ABCD = 15 + 9 + 15 + 9 = 48
AD:Perimeter of the ABCD = 9 : 48 = 3 : 16
Learn more about ratios here:
https://brainly.com/question/19220252
#SPJ1
to obtain a smaller margin of error choose a larger confidence level. choose a smaller confidence level.om/input?i
Answers
To obtain a smaller margin of error, choose a smaller confidence level.
Margin of error is defined as the degree of the sampling errors in statistics. It can be calculated using the formula below.
MOE = z x (SD / √n)
where MOE = margin of error
z = found by using a z-score table
SD = sample standard deviation
n = sample size
Based on the formula, to reduce the margin of error, the z-score, z, must be small. In order to have a smaller value of z, the probability, p, should also be small. And to obtain a small probability, choose a smaller confidence level.
Hence, to reduce the margin of error, use a lower confidence level.
Learn more about margin of error here: brainly.com/question/10218601
#SPJ4
What is the order of the symmetry of the pizza shown below?
6
07
04
08
Answers
Answer:
6
Step-by-step explanation:
pizza has rotational symmetry of 60 degrees. Thus, the order of symmetry will be 6.
find the numerical cofficient and literal cofficient in 7xy
Answers
\(numerical \: coefficient \: = > 7 \\ \\ literal \: coefficient \: = > \: xy\)
hope that helps uh..☺
Name a number that is not a whole number, a number that is not an integer, a number that is not a rational number, and a number that is not an irrational number. Do not use the same number twice.
Answers
Answer:
10, 5, .75, π
Step-by-step explanation:
Answer:
10, 5, .75, π
Step-by-step explanation:
An atom of rhodium (Rh) has a diameter of about 2.7×10−8cm. If the atom is assumed to be a sphere, what is the volume in m3 of a single Rh atom?
Answers
Therefore, the volume of a single Rh atom is approximately 1.011 × 10^(-29) m^3.
The diameter of a single Rh atom is given as 2.7 × 10^(-8) cm. The radius of the atom, which is half of the diameter, is therefore:
r = 2.7 × 10^(-8) cm / 2 = 1.35 × 10^(-8) cm
To find the volume of the sphere, we can use the formula:
V = (4/3)πr^3
where π is the constant pi.
Substituting the values, we get:
V = (4/3)π(1.35 × 10^(-8) cm)^3
= 1.011 × 10^(-23) cm^3
However, the answer is required in m^3, so we need to convert cm^3 to m^3. We know that:
1 cm = 0.01 m
Therefore:
(1 cm)^3 = (0.01 m)^3
1 cm^3 = 1 × 10^(-6) m^3
Substituting this conversion factor, we get:
V = 1.011 × 10^(-23) cm^3 × 1 × 10^(-6) m^3/cm^3
= 1.011 × 10^(-29) m^3
To know more about volume,
https://brainly.com/question/1565950
#SPJ11
33. PROBLEM SOLVING How many revolutions does the smaller gear complete during a single revolution of the larger gear?

Answers
The required number of revolution for small gear is 2
The given figure is a circle,
Then,
Radius of big circle = 7
radius of small circle = 3
Since we know that perimeter of circle = 2πr
Therefore,
Perimeter of big circle = 2x7x(22/7)
= 44 square units
Perimeter of small circle = 2x3x(22/7)
= 18.84 square units
Now the umber of revolution for small gear to complete a single revolution of the larger gear = 44/18.84 = 2.33 ≈ 2
Hence, number of revolution = 2.
Learn more about the circle visit:
https://brainly.com/question/24810873
#SPJ1
when evaluating (6.28x10^12)/(3.14x10^4)
Answers
Answer:
2×\(10^{8}\)
or
200000000
Step-by-step explanation:
\(\frac{6.28*10^{12} }{3.14*10^4}\)
2×\(10^{8}\)
or
200000000
I am not able to solve this question
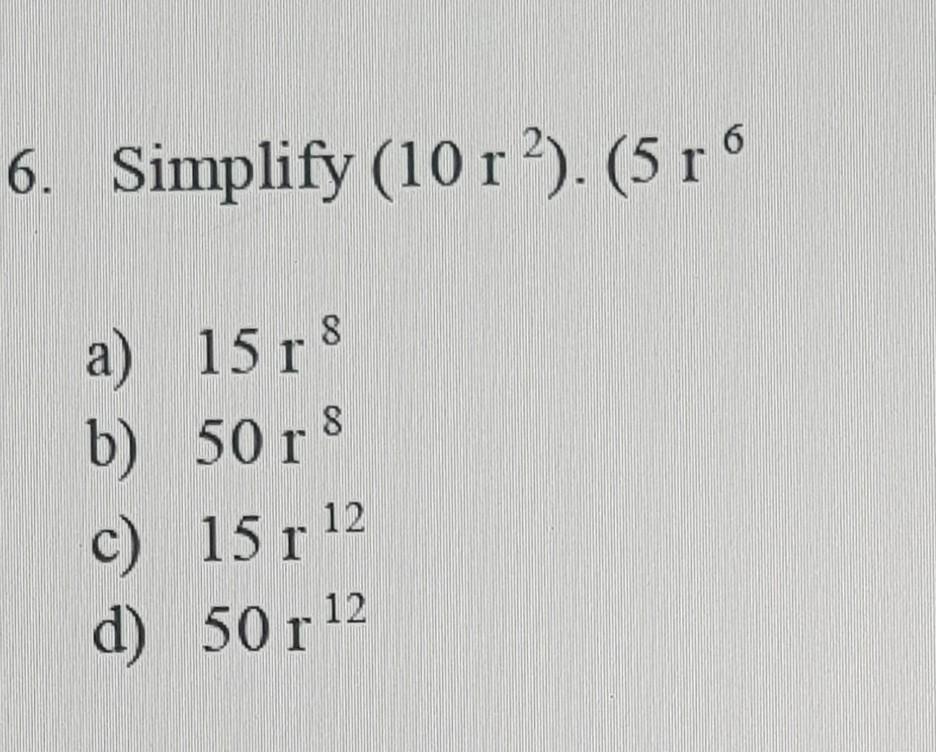
Answers
First, we multiply the numbers : 10 x 5 = 50
Now, we multiply r squared to r^6. To do this, we add the index numbers together : r^2 x r^6 = r^(2+6) = r^8
So, the answer is 50r^8, or b.
design a rectangular milk carton box of width w, length l, and height h which holds 512 cm3 of milk. the sides of the box cost 1 cent/cm2 and the top and bottom cost 2 cent/cm2. find the dimensions of the box that minimize the total cost of materials used.
Answers
The dimensions of the box that minimize the total cost of materials used are:
L = W = 16 cm
H = 32 cm
What is the rectangular dimension?
Two dimensions make up a rectangle: the length and, perpendicular to that, the breadth. A triangle's or an oval's interior likewise has two dimensions.
We have,
volume L* W * H = 512 cm³
sides of the box cost = 1 cent/cm²
top and bottom cost 2 cent/cm²
to find out
dimensions of the box that minimize the total cost of material use
we know here,
L* W * H = 512 cm³
where,
L is length and W is width and H is the height
so when we minimize the cost function
C( L, W, H ) = (1) 1 H ( L + W ) + (2) 1 L W
so put here H
substitute \(H = \frac{512}{LW}\) we get,
C(L, W) = 512(\(\frac{1}{l}, \frac{1}{W}\)) + 2LW
so
minimum cost will be when the two partial derivatives is 0
dC/dL = 2W - 512/L² = 0
so
dC/dW = 2L - 512/W² = 0
L = 256/W²
so
by solving the above equation we get
L = W = (256)⁻³ = 16cm
and
H = 512/16 = 32
H = 32 cm
Hence, the dimensions of the box that minimize the total cost of materials used are:
L = W = 16 cm
H = 32 cm
To learn more about the rectangular dimension visit,
https://brainly.com/question/27404871
#SPJ4
need help asappppppp
Answers
An irrational number is a real number that cannot be expressed as a ratio of integers. The decimal expansion of an irrational number is neither terminating nor recurring.
Let us check the options one at a time:
OPTION A: -√196
What are the solutions to the equation 7x² + 3x – 4 = 0?
Answers
x = 4/7 and x = -1
i need help plsssssssss

Answers
5 )
x^2 = 5^2 + 5^2
x^2 = 2 × 5^2
x = √( 2 × 5^2 )
x = 5√2 cm
_____________
6 )
x^2 = 30^2 + 40^2
x^2 = 900 + 1600
x^2 = 2500
x = √2500
x = 50 yards
1. Jordan is working two summer jobs, making $15
per hour walking dogs and making $25 per hour
clearing tables. In a given week, he can work a
maximum of 32 total hours and must earn at least
$168. If x represents the number of hours walking
dogs and y represents the number of hours clearing
tables, write a system of inequalities that represents
this scenario. The inequalities should have y
isolated.
Answers
The system of inequalities is y ≤ 32 - x and y ≥ (168 - 15x)/25.
Jordan is working for two summer jobs. The amount made per hour by walking dogs is $15. The amount made per hour by clearing tables is $25. Jordan can work for a maximum of 32 hours a week. He must earn at least $168.
The number of hours spent walking dogs is represented by "x". The number of hours spent clearing tables is represented by "y". The inequalities formed are :
x + y ≤ 32
15x + 25y ≥ 168
The graph of the common shaded region is attached below. The solutions lie in the first quadrant, where the region is shaded for both the inequalities.
To learn more about inequalities, visit :
https://brainly.com/question/28823603
#SPJ1

Slope of (-3,7) and (-7,13)
Answers
Answer:
slope = - \(\frac{3}{2}\)
Step-by-step explanation:
Calculate the slope m using the slope formula
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = (- 3, 7 ) and (x₂, y₂ ) = (- 7, 13 )
m = \(\frac{13-7}{-7-(-3)}\) = \(\frac{6}{-7+3}\) = \(\frac{6}{-4}\) = - \(\frac{3}{2}\)
What is the area of this shape??
Answers
Giving out 100 POINTS FOR THIS QUESTION!! Please don’t write nfoenwownw or something like that for the points!! I really need help! I WILL MARK BRAINLIEST!
What are the x-intercepts of the quadratic function shown?
A) (-1, -2)
B) (3,-4) and (-5,-4)
C) (1, 0) and (-3, 0)
D) (0, 1) and (0, -3)

Answers
Answer:
C) (1,0), and (-3,0)
Step-by-step explanation:
The parabola intercepts the x axis at points (1,0) and (-3,0).
your answer is
C) (1,0), and (-3,0)
have a good dayyy!
In 2012, gallup asked participants if they had exercised more than 30 minutes a day for three days out of the week. Suppose that random samples of 100 respondents were selected from both vermont and hawaii. From the survey, vermont had 65. 3% who said yes and hawaii had 62. 2% who said yes. What is the value of the sample proportion of people from vermont who exercised for at least 30 minutes a day 3 days a week?.
Answers
The value of the sample proportion of people from Vermont who exercised for at least 30 minutes a day 3 days a week is 0.653, which is equivalent to 65.3%.
It is important to note that this value is based on a random sample of respondents and may not necessarily represent the true proportion of the entire population of Vermont who exercise regularly.
To find the sample proportion of people from Vermont who exercised for at least 30 minutes a day, 3 days a week, follow these steps:
1. Convert the given percentage (65.3%) to a decimal by dividing by 100: 65.3 / 100 = 0.653
2. Multiply the decimal by the number of participants in the random sample (100 respondents): 0.653 * 100 = 65.3
3. Round the result to the nearest whole number to find the number of participants who exercised: 65.3 ≈ 65
4. Divide the number of participants who exercised (65) by the total number of participants in the random sample (100): 65 / 100 = 0.65
This means that out of the 100 participants sampled from Vermont, 65.3 of them answered "yes" to the question of whether they had exercised for more than 30 minutes a day for three days out of the week.
The value of the sample proportion of people from Vermont who exercised for at least 30 minutes a day, 3 days a week is 0.65 or 65%.
Learn more about sample proportion here:
brainly.com/question/29912751
#SPJ11
During a 12-hour period, the temperature rose by 48*f. The temperature rose the same number of degrees each hour. How many degrees did the temperature rise each hour?
Answers
Answer:
4 degrees per hour
Step-by-step explanation:
48 degrees per 12 hours = 48/12 degrees per hour = 4 degrees per hour
Select the correct formula to solve for x.
cos (33) = x/14
sin (33) = x/14
cos (33) = 14/x
sin (33) = 14/x

Answers
Answer: Choice B) sin (33) = x/14
This is because the sine of an angle is equal to the opposite side over the hypotenuse
sin(angle) = opposite/hypotenuse
sin(33) = x/14
We can't use cosine because we don't have a variable for the adjacent side.
Help me calculate the perimeter of this shape!

Answers
Answer:
32mm
Step-by-step explanation:
6 + 8 + 6 + 12 = 32mm
Answer:
32 mmStep-by-step explanation:
P = a + b + c + da = base
b = base
c = side
d = side
P = 8 + 12 + 6 + 6 = 32 mmDetermine whether these are valid arguments.a) If x is a positive real number, then x² is a positive real number. Therefore, if a² is positive, where a is a real number, then a is a positive real number.b) If x² ≠ 0, where x is a real number, then x ≠ 0. Let a be a real number with a² ≠ 0; then a ≠ 0.
Answers
The given argument is " If x is a positive real number, then x² is a positive real number." is invalid. Because if a² is positive, it is not always true that a is a positive real number. The given argument is " If x² ≠ 0, where x is a real number, then x ≠ 0. Let a be a real number with a² ≠ 0; then a ≠ 0." is valid argument. Because if a is real number so a² is also a real number.
If x is a positive real number, then x² is a positive real number. Therefore, if a² is positive, where a is a real number, then a is a positive real number. This is an invalid argument. The premise states that if x is a positive real number, then x² is a positive real number, which is true. However, the conclusion that if a² is positive, then a is a positive real number does not necessarily follow from the premise. For example, if a is -2, then a² is positive, but a is not a positive real number.
If x² ≠ 0, where x is a real number, then x ≠ 0. Let a be a real number with a² ≠ 0; then a ≠ 0. This is a valid argument. The premise states that if x² ≠ 0, then x ≠ 0, which is true since the only way for x² to be equal to zero is if x is equal to zero. The conclusion that if a² ≠ 0, then a ≠ 0 follows logically from the premise, since a is a real number and the same logic applies to a² as to x².
To know more about real number:
https://brainly.com/question/551408
#SPJ4
what is it tell me please

Answers
Answer:
19.995
Step-by-step explanation:
-6f + 2s + 3 - 8 use f = 9 and s = 6
Answers
Answer:
-47
Step-by-step explanation:
-6(9) + 2(6) + 3 - 8
-54 + 12 + 3 - 8
-42 + 3 - 8
-39 - 8
-47
Pllzzz answerrrr......

Answers
Answer:
A. √2 > 1
Step-by-step explanation:
A: The √2 is more than one but less than 2. It's approximated as 1.414. This answer choice is correct.
B: The √4 is 2, which is less than π. Pi is approximated as 3.141. Therefore, this answer choice is incorrect.
C: The √2 is less than pi but greater than one. It's approximated as 1.414. This answer choice is incorrect.
D: The √3 is less than 2 but greater than one. It's approximated as 1.732. Therefore, this is incorrect.
Therefore, the correct answer is A. √2 > 1.
which are not the length of sides of a right

Answers
Answer:
D.
Step-by-step explanation:
all numbers except d are pythagorean triples, hope this helps!!
6.1 Colby bought a laptop worth Rx for his university studies. The value of the laptop decreased at r% per annum using the reducing balance method. After 4 years, the value of the laptop was worth 31 of its original price. Calculate r, the rate of depreciation.
6.2 On 1 February 2014 , Ncominkosi took a loan from a bank to buy a car. His first payment for the loan was due on 31 July 2014 . Once he started paying the loan, it took him 6 years to fully pay the loan at an interest rate of 9,5% p.a. compounded monthly. In total, he paid the bank R596 458,10.
6.2.1 How much was his monthly instalment?
6.2.2 How much money did he borrow from the bank? Write down your answer to the nearest rand.
Answers
6.1). the rate of depreciation, r, is approximately 10.77%.
6.2.1). Ncominkosi's monthly installment amount was approximately R 10,505.29.
6.2.2). Ncominkosi borrowed approximately R 377,510.83 from the bank.
6.1) Let's assume the original price of the laptop is P. According to the reducing balance method, the value of the laptop after 4 years can be calculated as P * (1 - r/100)^4. We are given that this value is 31% of the original price, so we can write the equation as P * (1 - r/100)^4 = 0.31P.
Simplifying the equation, we get (1 - r/100)^4 = 0.31. Taking the fourth root on both sides, we have 1 - r/100 = ∛0.31.
Solving for r, we find r/100 = 1 - ∛0.31. Multiplying both sides by 100, we get r = 100 - 100∛0.31.
Therefore, the rate of depreciation, r, is approximately 10.77%.
6.2.1) To determine the monthly installment amount, we can use the formula for calculating the monthly payment on a loan with compound interest. The formula is as follows:
\(P = \frac{r(PV)}{1-(1+r)^{-n}}\)
Where:
P = Monthly payment
PV = Loan principal amount
r = Monthly interest rate
n = Total number of monthly payments
Let's calculate the monthly installment amount for Ncominkosi's loan:
Loan amount = Total amount paid to the bank - Interest
Loan amount = R 596,458.10 - R 0 (No interest is deducted from the total paid amount since it is the total amount paid)
Monthly interest rate = Annual interest rate / 12
Monthly interest rate = 9.5% / 12 = 0.0079167 (rounded to 7 decimal places)
Number of monthly payments = 6 years * 12 months/year = 72 months
Using the formula mentioned above:
\(P = \frac{0.0079167(Loan Amount}{1-(1+0.0079167)^{-72}}\)
Substituting the values:
\(P = \frac{0.0079167(596458.10}{1-(1+0.0079167)^{-72}}\)
Calculating the value:
P≈R10,505.29
Therefore, Ncominkosi's monthly installment amount was approximately R 10,505.29.
6.2.2) To determine the amount of money Ncominkosi borrowed from the bank, we can subtract the interest from the total amount he paid to the bank.
Total amount paid to the bank: R 596,458.10
Since the total amount paid includes both the loan principal and the interest, and we need to find the loan principal amount, we can subtract the interest from the total amount.
Since the interest rate is compounded monthly, we can use the compound interest formula to calculate the interest:
\(A=P(1+r/n)(n*t)\)
Where:
A = Total amount paid
P = Loan principal amount
r = Annual interest rate
n = Number of compounding periods per year
t = Number of years
We can rearrange the formula to solve for the loan principal:
\(P=\frac{A}{(1+r/n)(n*t)}\)
Substituting the values:
Loan principal (P) = \(\frac{596458.10}{(1+0.095/12)(12*6)}\)
Calculating the value:
Loan principal (P) ≈ R 377,510.83
Therefore, Ncominkosi borrowed approximately R 377,510.83 from the bank.
Learn more about interest rate here:
https://brainly.com/question/14599912
#SPJ11
Sam found that is the product of 5 and a number is increased by 8 the result is 10 more than the product of 3 and the number what is the number
Answers
In this case, we'll have to carry out several steps to find the solution.
Step 01:
Data
number = x = ?
Step 02:
x = number
5 * x + 8 = 10 + 3 * x
5x + 8 = 10 + 3x
5x - 3x = 10 - 8
2x = 2
x = 2 / 2 = 1
The answer is:
The number is 1
What is the volume of the prism, in cubic feet?

Answers
Answer:
(1/2)(4)(6)(12.5) = 12(12.5) = 150 ft²
Use the Divergence Theorem to compute the net outward flux of the vector field F = (x², - y², z²) across the boundary of the region D, where D is the region in the first octant between the planes z = 9 - x - y and z = 6 - x - y.
Answers
To apply the Divergence Theorem, we need to first find the divergence of the vector field F:
div(F) = ∂/∂x(x²) + ∂/∂y(-y²) + ∂/∂z(z²)
= 2x - 2y + 2z
Next, we find the bounds for the region D by setting the two plane equations equal to each other and solving for z:
9 - x - y = 6 - x - y
z = 3
So the region D is bounded below by the xy-plane, above by the plane z = 3, and by the coordinate planes x = 0, y = 0, and z = 0. Therefore, we can set up the integral using the Divergence Theorem as follows:
∫∫F · dS = ∭div(F) dV
= ∭(2x - 2y + 2z) dV
= ∫₀³ ∫₀^(3-z) ∫₀^(3-x-y) (2x - 2y + 2z) dz dy dx
We can simplify this integral using the limits of integration to get:
∫∫F · dS = ∫₀³ ∫₀^(3-x) ∫₀^(3-x-y) (2x - 2y + 2z) dz dy dx
= ∫₀³ ∫₀^(3-x) [(2x - 2y)(3-x-y) + (2/3)(3-x-y)³] dy dx
= ∫₀³ [∫₀^(3-x) (2x - 2y)(3-x-y) dy + ∫₀^(3-x) (2/3)(3-x-y)³ dy] dx
Evaluating the two inner integrals, we get:
∫₀^(3-x) (2x - 2y)(3-x-y) dy = -x²(3-x) + (3/2)x(3-x)²
∫₀^(3-x) (2/3)(3-x-y)³ dy = (2/27)(3-x)⁴
Substituting these back into the integral and evaluating, we get:
∫∫F · dS = ∫₀³ [-x²(3-x) + (3/2)x(3-x)² + (2/27)(3-x)⁴] dx
= 9/5
Therefore, the net outward flux of the vector field F across the boundary of the region D is 9/5.
Learn more about Divergence Theorem from
https://brainly.com/question/17177764
#SPJ11
