12 is 3/4 of what number
Answers
Answer:
Step by step: you need to divide the top and multiple by the bottom. 12 divided by 3 is 4, and 4 times 4 is 16
Answer:
16
Step-by-step explanation:
The formula to solve for this is \(\frac{is}{of}=\frac{percent}{100}\)
Here the 12 is our "is", the "of" is the \(\frac{3}{4}\) , and the "percent" is what we are solving for so we can replace it for "x"
So now replacing our values we have \(\frac{12}{\frac{3}{4} } =\frac{x}{100}\)
Cross multiplying we get \((12)(100) = (x)(\frac{3}{4} )\)
Which then simplifies to
Then multiplying both sides by 4 to get rid of the fraction we get 4800% = 3x
The we need to divide by 3 and we get 1600% = x
Now this is in a percentage, so we need to divide 1600 by 100 to turn it into a whole number which comes out to x = 16
Related Questions
324.56 × 54.82
SHOW YOUR WORK
ALL OF IT PLEASE AND THANK YOU!
PLEASE HURRY!
Answers
Answer:
17792.3792
Step-by-step explanation:
:))))))
use the law of exponents to simplify the following expression

Answers
Answer:
5x⁴
Step-by-step explanation:
10x⁸÷2x⁴=
5x⁴
Using integration by parts, rewrite the following integral as fudv = uv-fvdu [in (2x) e 4x² dx
Answers
To rewrite the integral ∫(2x)\(e^{4x^{2} }\)dx using integration by parts, we'll consider the function f(x) = (2x) and g'(x) = \(e^{4x^{2} }\).
Integration by parts states that ∫u dv = uv - ∫v du, where u and v are functions of x.
Let's assign:
u = (2x) => du = 2 dx
dv = \(e^{4x^{2} }\) dx => v = ∫\(e^{4x^{2} }\) dx
To evaluate the integral of v, we need to use a technique called the error function (erf). The integral cannot be expressed in terms of elementary functions. Hence, we'll express the integral as follows:
∫\(e^{4x^{2} }\) dx = √(π/4) × erf(2x)
Now, we can rewrite the integral using integration by parts:
∫(2x)\(e^{4x^{2} }\) dx = uv - ∫v du
= (2x) × (√(π/4) × erf(2x)) - ∫√(π/4) × erf(2x) × 2 dx
= (2x) × (√(π/4) × erf(2x)) - 2√(π/4) × ∫erf(2x) dx
The integral ∫erf(2x) dx can be further simplified using substitution. Let's assign z = 2x, which implies dz = 2 dx. Substituting these values, we get:
∫erf(2x) dx = ∫erf(z) (dz/2) = (1/2) ∫erf(z) dz
Therefore, the final expression becomes:
∫(2x)\(e^{4x^{2} }\) dx = (2x) × (√(π/4) × erf(2x)) - √(π/2) × ∫erf(z) dz
Please note that the integral involving the error function cannot be expressed in terms of elementary functions and requires numerical or tabulated methods for evaluation.
Learn more about integral here:
https://brainly.com/question/31109342
#SPJ11
if a is an n × n matrix having linearly independent eigenvectors v1, v2, . . . , vn, then the n × n matrix p = [ v1 v2 . . . vn ] T/F
Answers
True. If matrix A is an n × n matrix with linearly independent eigenvectors v1, v2, ..., vn, then the n × n matrix P = [v1 v2 ... vn] forms a matrix of eigenvectors. In other words, the columns of matrix P are the eigenvectors of matrix A.
1. When a matrix A has linearly independent eigenvectors v1, v2, ..., vn, it means that each eigenvector corresponds to a distinct eigenvalue. The eigenvectors span the entire vector space of dimension n.
2. The matrix P = [v1 v2 ... vn] is constructed by arranging the eigenvectors v1, v2, ..., vn as columns. Since the eigenvectors are linearly independent, the matrix P formed by these columns is invertible.
3. When we multiply matrix P by its inverse P^(-1), we obtain the identity matrix I. This implies that P^(-1) exists and is the inverse of P.
4. Now, let's consider the equation A * P = P * D, where D is a diagonal matrix that contains the eigenvalues corresponding to the eigenvectors v1, v2, ..., vn along its diagonal.
5. Multiplying both sides of the equation by P^(-1) from the left, we get P^(-1) * A * P = P^(-1) * P * D, which simplifies to P^(-1) * A * P = D.
6. Since P^(-1) exists, we can rewrite the equation as A = P * D * P^(-1). This equation shows that matrix A can be diagonalized using the matrix P formed by the eigenvectors and its inverse P^(-1).
7. Therefore, matrix P = [v1 v2 ... vn] is indeed an n × n matrix consisting of linearly independent eigenvectors of matrix A.
learn more about linearly independent eigenvectors here: brainly.com/question/32355061
#SPJ11
Jon won 30 marbles playing horseshoes at a game night. Later, he gave 3 to each of his friends. He only has 9 left. How many friends does she have?
Answers
30 marbles minus the 9 she has left is 21
21 divided by 3 per friend is 7 friends
In angle ABC the measure of Angle B is 13 more than the measure of Angle A and the measure of angle C is 9 less than twice the measure of angle A find the measure of each angle in ABC. only an algebraic will be accepted.
Answers
Answer:
its b
Step-by-step explanation:
its
-2.2f + 0.2f - 11 - 3 =
Answers
Answer:
-2f-14
Step-by-step explanation:
Answer:
-2f-14 is your answer pls give brainlist
Step-by-step explanation:
twenty-seven percent of primary care doctors think their patients receive unnecessary medical care. if required, round your answer to four decimal places.
Answers
Incomplete question.No requirement of question
simplify by combining terms:
3 (4x + 5) + 2
Answers
Answer:
Step-by-step explanation:
First you distribute the 3 to the numbers in the parentheses: 12x + 15. Then simplify 12x + 15 + 2 = 12x + 17
Joey intends to roll a six-sided number cube 100 times. What probability model can he use to predict whether or not each roll will give a result that is divisible by 3?
Answers
Options :
A. Each roll has a 0.117 probability of being divisible by 3.
B. Each roll has a 0.333 probability of being divisible by 3.
C. Each roll has a 0.5 probability of being divisible by 3. D. Each roll has a 0.667 probability of being divisible by 3.
Answer: B. Each roll has a 0.333 probability of being divisible by 3.
Step-by-step explanation:
Sample space for a six-sided number cube :
1, 2, 3, 4, 5, 6
Number of outcomes divisible by 3:
(3, 6) = 2
Probability of an event = Number of required outcomes / total number of possible items
Probability (getting a number divisible by 3):
(Number of outcomes divisible by 3 / total outcomes in sample space)
Probability (getting a number divisible by 3):
2 / 6 = 1/3
= 0.333
How many solutions does the system of equations below have? y = 2x – 10 y = 2x – 10 - no solution one solution infinitely many solutions
Answers
Answer:
11/2y
Step-by-step explanation:
Let's solve for x.
y=2x−10y
Step 1: Flip the equation.
2x−10y=y
Step 2: Add 10y to both sides.
2x−10y+10y=y+10y
2x=11y
Step 3: Divide both sides by 2.
2x
2
=
11y
2
x=
11
2
y
Answer:
11/2y.....................
What is the quotient of the following division problem?
14624÷181 = ?
OA. 80 r145
OB. 80 r144
OC. 79 r144
OD. 82 r143
Answers
Answer:
b is the correct answer
80r144
Step-by-step explanation:
Find the center and radius of the circle
x2 + 2x - 1 + y2+ 4y = 3
Answers
Answer:R=3\\
(a,b)=(1,2)
Step-by-step explanation:
\((x-a)^{2}+(y-b)^{2}=R^{2}\\(a,b)-center\\R-radius\\x^{2} + 2x - 1 + y^{2}+ 4y = 3\\(x+1)^2=x^{2}+2x+1\\(y+2)^{2}=y^{2}+ 4y+4\\x^{2} + 2x - 1 + y^{2}+ 4y = (x+1)^2-1+(y+2)^2-4-1=(x+1)^2+(y+2)^2-6=3\\(x+1)^2+(y+2)^2=9\\R=3\\(a,b)=(1,2)\)
A circle is divided into two sectors in the ratio 3:7. If the radius of the circle is 7cm, calculate the length of the minor arc of the circle
Answers
Answer:
13.2cm
Step-by-step explanation:
SEE THE IMAGE FOR SOLUTION
HOPE IT HELPS
HAVE A GREAT DAY
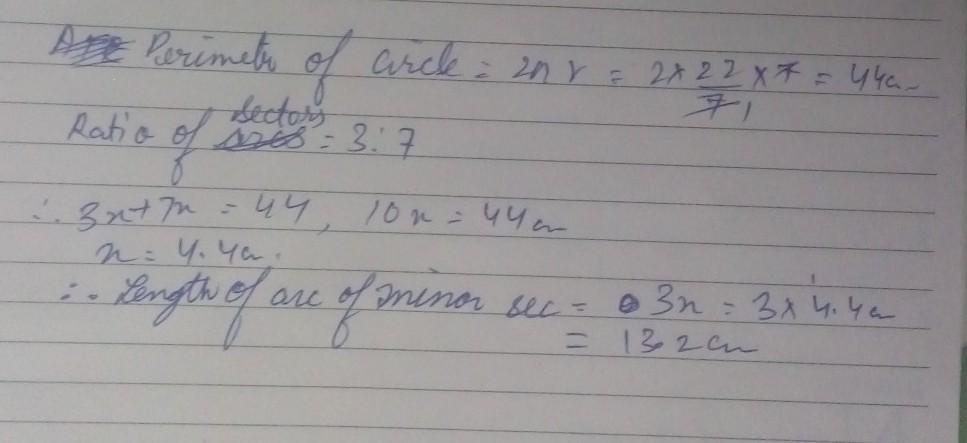
Explanation:
2 x pi x r = P
P = 2 x 22/7 x 7
P = 44cm
Length of minor arc = P x 3/10 = 44 x 3/10 = 13.2 cm
each tile in the model represents 1/4. How many titles make a group of 3/4
Answers
Answer:
3 tiles
because 1/4+1/4+1/4=3/4
I hope this helps you!
Find the missing side of the Triangle

Answers
Answer:
\(\sqrt{193}\)
Step-by-step explanation:
\(c^2=a^2+b^2\\c^2=12^2+7^2\\c^2=144+49\\c^2=193\\c=\sqrt{193}\)
Answer:
x = \(\sqrt{193}\)
Step-by-step explanation:
The given is a right triangle and in right triangles the square value of hypotenuse is equal to sum of other two side lengths' square value
12^2 + 7^2 = x^2
144 + 49 = x^2
193 = x^2
x = \(\sqrt{193}\)
What is the domain of ggg? Choose 1 answer: Choose 1 answer: (Choice A) A The xxx-values -7−7minus, 7, -4−4minus, 4, 000, 333, and 444 (Choice B) B -4 \leq x \leq 8−4≤x≤8minus, 4, is less than or equal to, x, is less than or equal to, 8 (Choice C) C The xxx-values -4−4minus, 4, -3−3minus, 3, 000, 222, and 888 (Choice D) D -7 \leq x \leq 4−7≤x≤4
Answers
The domain of ggg is option D: -7 ≤ x ≤ 4.
To determine the domain of a function, we need to identify the set of all possible values for the independent variable, in this case, x, for which the function is defined.
In option D, the domain is specified as -7 ≤ x ≤ 4. This means that x can take any value within the closed interval from -7 to 4, inclusive.
In other words, the domain of ggg includes all real numbers between -7 and 4, including -7 and 4 themselves. This interval represents the range of values for x that satisfy the given conditions for the function ggg.
Learn more about function from
https://brainly.com/question/11624077
#SPJ11
what is the probability of having four girls in a row?
Answers
Answer:
21 or 10
Step-by-step explanation:
I
Need to get myself together, I'm a mess
In Bikini Bottom, I'm with Sandy
Moesha keep on drinkin' all the brandy
Keisha eat the molly like it's candy
URGENT!! If the probability of getting heads from a coin is 1/2, what is the probability that if you flip the coin ten times it will be heads.
Answers
Answer:
Based on the calculations we just did, you expect that if you toss a coin 10 times, it will land on heads 50% of the time.
Answer:
The probability of getting heads from a coin is 1/2. If you flip the coin ten times, the probability that it will be heads every time is (1/2)^10 = 1/1024.
However, if you are asking for the probability of getting at least one head in ten flips, then you can use the complement rule to find the probability of getting no heads and subtract it from 1. The probability of getting no heads in ten flips is (1/2)^10 = 1/1024, so the probability of getting at least one head is 1 - 1/1024 = 1023/1024, which is approximately 0.999.
7. Ifa = 3an * db = - 2 . find the values of: (a + b)ab
Answers
The Values of (a+b)ab are undefined.
Given that, a = 3an and db = -2We need to find the values of (a+b)
Now, we have a = 3an... equation (1)Also, we have db = -2... equation (2)From equation (1), we get: n = 1/3... equation (3)Putting equation (3) in equation (1), we get: a = a/3a = 3... equation (4)Now, putting equation (4) in equation (1), we get: a = 3an... 3 = 3(1/3)n = 1
From equation (2), we have: db = -2=> d = -2/b... equation (5)Multiplying equation (1) and equation (2), we get: a*db = 3an * -2=> ab = -6n... equation (6)Putting values of n and a in equation (6), we get: ab = -6*1=> ab = -6... equation (7)Now, we need to find the value of (a+b).For this, we add equations (1) and (5),
we get a + d = 3an - 2/b=> a + (-2/b) = 3a(1) - 2/b=> a - 3a + 2/b = -2/b=> -2a + 2/b = -2/b=> -2a = 0=> a = 0From equation (1), we have a = 3an=> 0 = 3(1/3)n=> n = 0
Therefore, from equation (5), we have:d = -2/b=> 0 = -2/b=> b = ∞Now, we know that (a+b)ab = (0+∞)(0*∞) = undefined
Therefore, the values of (a+b)ab are undefined.
For more questions on Values .
https://brainly.com/question/843074
#SPJ8
I don't understand which one I'll give brainiest

Answers
Answer:
Step-by-step explanation:
The answer should be the one on the top
Answer:
remember a tip, negetive and positive is a negative number, and a negative and a negative is a positive number
Step-by-step explanation:
Hope this helps :D
I need this practice problem explained I will provide a picture with the answer options


Answers
Given the following System of Equations:
\(\begin{cases}x+2y=8 \\ -3x-2y=12\end{cases}\)You can solve it with Cramer's Rule. The steps are shown below:
1. By definition, you know that for "x"
\(x=\frac{D}{D_x}=\frac{\begin{bmatrix}{c_1} & {b_1} & {} \\ {c_2_{}_{}_{}} & {b_2} & {} \\ {} & {} & \end{bmatrix}}{\begin{bmatrix}{a1_{}} & {b_1} & {} \\ {a_2_{}} & {b_2} & {} \\ {} & {} & \end{bmatrix}}\)In this case:
\(\begin{gathered} c_1=8 \\ c_2=12_{} \\ b_1=2 \\ b_2=-2_{} \\ a_1=1 \\ a_2=-3 \end{gathered}\)Then, you can substitute values and evaluating, you get that the value of "x" is:
\(x=\frac{\begin{bmatrix}{8_{}} & {2_{}} & {} \\ {12_{}} & {-2_{}} & {} \\ {} & {} & \end{bmatrix}}{\begin{bmatrix}{1_{}} & {2_{}} & {} \\ {-3_{}} & {-2_{}} & {} \\ {} & {} & \end{bmatrix}}=\frac{(-2)(8)-(2)(12)}{(-2)(1)-(2)(-3)}=\frac{-16-24}{-2+6}=-10\)2. By definition, for "y":
\(y=\frac{D_y}{D}=\frac{\begin{bmatrix}{a_1} & {c_1} & {} \\ {a_2} & {c_2} & {} \\ {} & {} & {}\end{bmatrix}}{\begin{bmatrix}{a_1} & {b_1} & {} \\ {a_2} & {b_2} & {} \\ {} & {} & {}\end{bmatrix}}\)Knowing the values, substitute and evaluate:
\(y=\frac{\begin{bmatrix}{1_{}} & {8_{}} & {} \\ {-3_{}} & {12_{}} & {} \\ {} & {} & {}\end{bmatrix}}{\begin{bmatrix}{1_{}} & {2_{}} & {} \\ {-3_{}} & {-2_{}} & {} \\ {} & {} & {}\end{bmatrix}}=\frac{(12)(1)-(-3)(8)}{(-2)(1)-(-3)(2)}=\frac{12+24}{-2+6}=9\)Therefore, the answer is:
\(\begin{gathered} x=\frac{\begin{bmatrix}{8_{}} & {2_{}} & {} \\ {12_{}} & {-2_{}} & {} \\ {} & {} & \end{bmatrix}}{\begin{bmatrix}{1_{}} & {2_{}} & {} \\ {-3_{}} & {-2_{}} & {} \\ {} & {} & \end{bmatrix}}=\frac{-16-24}{-2+6}=-10 \\ \\ \\ y=\frac{\begin{bmatrix}{1_{}} & {8_{}} & {} \\ {-3_{}} & {12_{}} & {} \\ {} & {} & {}\end{bmatrix}}{\begin{bmatrix}{1_{}} & {2_{}} & {} \\ {-3_{}} & {-2_{}} & {} \\ {} & {} & {}\end{bmatrix}}=\frac{12+24}{-2+6}=9 \end{gathered}\)h(t)=−16t2+24t+40, how long does it take to fall to the ground?
Answers
Answer:
2.5 seconds
Step-by-step explanation:
h will be 0 when it hits the ground
0 = -16t^2 + 24t + 40
use Quadratic Formula to find t = 2.5 seconds
The volume of this cube is 125 cubic feet. What is the value of u?
Answers
I'm confused but If you're asking what would be the length of the cube I'll say your answer would be 5 srry
Evaluate Jxy dx + (x + y)dy along the curve y=x^2 from (-1,1) to (2,4).
Answers
The value of the line integral is 303/20, or approximately 15.15.
We need to evaluate the line integral Jxy dx + (x + y)dy along the curve y=x^2 from (-1,1) to (2,4).
Parametrizing the curve as x=t and y=t^2, we get the following limits of integration:
t ranges from -1 to 2.
Substituting x=t and y=t^2 in the given expression, we get:
Jxy dx + (x + y)dy = t(t^2) dt + (t + t^2) 2t dt = (t^3 + 2t^3 + 2t^4) dt = (3t^3 + 2t^4) dt
Integrating this expression with respect to t from -1 to 2, we get:
∫(-1)²^(4) (3t³ + 2t⁴) dt = [3/4 * t^4 + 2/5 * t^5] between -1 and 2
= (3/4 * 2^4 + 2/5 * 2^5) - (3/4 * (-1)^4 + 2/5 * (-1)^5)
= (3/4 * 16 + 2/5 * 32) - (3/4 * 1 + 2/5 * (-1))
= 12 + 51/20 = 252/20 + 51/20 = 303/20
The value of the line integral is 303/20, or approximately 15.15.
Know more about integral here:
https://brainly.com/question/18125359
#SPJ11
To the nearest whole percent, what is the probability that a randomly chosen member of the JV swim team does not wear glasses and is in the 10th grade? 14% 17% 55% 67%
Answers
Answer: 14%
Step-by-step explanation:
Complete question is provided in the attachment below:
Probability that members of the junior varsity swim team wear glasses = 55%=0.55
Given: P(wear glasses) = 0.55
P(not wear glasses) = 1-0.55 = 0.45
P(member in 10th grade | not wear glasses) = 30%
Using conditional probability formula:
\(P(B|A)=\dfrac{P(A\text{ and } B)}{P(A)}\)
\(\Rightarrow\ 0.30=\dfrac{P(\text{not wear glasses and in 10th grade})}{0.45}\\\\\Rightarrow\ P(\text{not wear glasses and in 10th grade})=0.45\times0.30\\\\0.135=13.5\%\approx14\%\)
Hence, the probability that a randomly chosen member of the JV swim team does not wear glasses and is in the 10th grade = 14%.
So, the correct option is "14%".

The equation above shows how temperature F, measured in degrees Fahrenheit, relates to a temperature C, measured in degrees Celsius. Based on the equation, which of the following must be true?
l. A temperature increase of 1 degree Fahrenheit is equivalent to a temperature increase of 5/9 degree Celsius.
ll. A temperature increase of 1 degree Celsius is equivalent to a temperature increase of 1.8 degrees Fahrenheit.
lll. A temperature increase of 5/9 degree Fahrenheit is equivalent to a temperature increase of 1 degree Celsius.
A) I only
B) II only
C) III only
D) I and II only

Answers
Answer:
D. I and II only
Step-by-step explanation:
Give:- C= 5/9( f - 32 )
--> F = 9/5c + 32
(I) If F' = F + 1
C' = 5/9( F' - 32)
C' = 5/9( F - 32) + 5/9 x 1
C' = C + 5/9
The temperature increase of 1 degree Fahrenheit is equivalent to a temperature increase of 5/9 degree Celsius
THEREFORE, STATEMENT | IS TRUE.
(II) If C'= C + 1
F' = 9/5C' + 32
F' = ( 9/5C + 32 ) + 9/5
F' = F + 9/5
F' = F + 1.8
The temperature increase of 1 degree Celsius is equivalent to a temperature increase of 1.8 degrees Fahrenheit.
THEREFORE, STATMENT || IS TRUE
(III) If F' = F + 5/9
C' = 5/9 (F' - 32)
C' = 5/9 ( F - 32 ) + 5/9 x 5/9
C' = C + 25/81
The temperature increase of 5/9 degrees Fahrenheit is equivalent to a temperature increase of 25/81 degree Celsius.
THEREFORE, STATEMENT ||| IS FALSE
Hi, please help me with this question.
what is 45+46+47+ ... +53+54?
Answers
Answer:
245Step-by-step explanation:
1). 91 + 41 + 53 + 54 {Simplify}
2). 138 + 53 + 54 {Simplify}
3). 191 + 54 {Simplify}
4). 245 {Add}
9514 1404 393
Answer:
495
Step-by-step explanation:
There are several ways to figure this:
1) Multiply the average value by the number of numbers. The average number in an arithmetic sequence is the average of the first and last numbers in the sequence.
average = (54+45)/2 = 49.5
number of numbers = 54 -45 +1 = 10
Total = 49.5 · 10 = 495
__
2) Add the numbers pairwise. It works best to work toward the middle from the ends:
45 +54 = 99
46 +53 = 99
47 +52 = 99
48 +51 = 99
49 +50 = 99
Total = 5 · 99 = 495
__
3) Subtract the sum of numbers to 44 from the sum of numbers to 54.
The sum of numbers 1 to n is (n)(n+1)/2.
(54)(55)/2 -(44)(45)/2 = (27)(55) -(22)(45) = 1485 -990 = 495
__
4) Use a spreadsheet or calculator to add them. (see attached)

Which statement about 192° is correct?
A.
tan 192° < 0
B.
cos 192° > 0
C.
sin 192° < 0
Answers
Answer:
Step-by-step explanation:
192° is in quadrant III, so sin(192°) < 0, cos(192°) < 0, tan(192°) > 0
Answer:
C. sin 192° < 0
Step-by-step explanation:
see image below

Pls help its the last question

Answers
Answer:
I believe the answer is -60
Step-by-step explanation: