5. A student graphed f of x. equals. x. and g of x. equals. 1 over 3. f of x. plus 5 on the same coordinate grid. Which statements are true?
Select THREE correct answers.
To create g, the graph of f is shifted 5 units up.
To create g, the graph of f is shifted 5 units down.
The graph of f is steeper than the graph of g.
The graph of g is steeper than the graph of f.
The y-intercept of g is 5 units below the y-intercept of f.
The y-intercept of g is 5 units above the y-intercept of f.
Answers
The three correct answers that describe the given transformations are;
A) To create g, the graph of f is shifted 5 units up.
C) The graph of f is steeper than the graph of g.
F) The y-intercept of g is 5 units above the y-intercept of f.
How to find the sequence of transformation?We are given the equations as;
f(x) = x
g(x) = ¹/₃(f(x)) + 5
For a function f(x) we define a vertical translation (or vertical shift) of n units as:
g(x) = f(x) + n
If n is positive, the translation is upwards
If n is negative, the translation is downwards.
Thus, the graph of f was shifted 5 units upwards.
Now, the equation of a line in slope intercept form is;
y = mx + c
where;
m is slope
c is y-intercept
Thus;
y-intercept of f(x) = 0
y-intercept of g(x) = 5
Thus;
y -intercept of g is 5 units above y-intercept of f.
Now, the steeper the line, the higher the slope. Thus, function f has a higher slope than function g and so function f is steeper than function g.
Read more about sequence of transformation at; https://brainly.com/question/4289712
#SPJ1
Related Questions
if f(X+4) =3x+4 , then find the value of f(4)
please explain it clearly .
Answers
\(\\ \sf\longmapsto f(x+4)=3x+4\)
\(\\ \sf\longmapsto f(x)=3x+4-4\)
\(\\ \sf\longmapsto f(x)=3x\)
Now
\(\\ \sf\longmapsto f(4)\)
\(\\ \sf\longmapsto 3(4)\)
\(\\ \sf\longmapsto 12\)
Ezra enjoys gardening Every Sunflower plant he waters requires 0.7 liters of water, and every lily plant he waters requires 0.5 liters of water. He graphs
the number of surfower plants (S) and number of lily plants (L) to determine how many of each plants he can water with at most 11 liters
Which type of boundary line she he use in his graph?
Answers
Answer:
the answer is 8
Step-by-step explanation:
yes Ezra can plant 8 sunflowers
hope this helpsss :)
A fast food restaurant asks customers to evaluate the drive-thru service as good, average, or poor. Which level of measurement is this classification
Answers
The level of measurement used in the classification is ordinal.
Ordinal levels of measurement group variables into categories like nominal scales, but also convey the order of the variables. For example, rate pain on a scale of 1 to 5, or classify income as high, medium, or low.
An ordinal scale is a second-level measure that indicates the ranking and order of data without actually specifying the degree of variation among the data. The order measurement level is his second of the four measurement scales. "Ordinal" means "order".
Learn more about ordinal here: https://brainly.com/question/4823744
#SPJ4
help me find the answer please
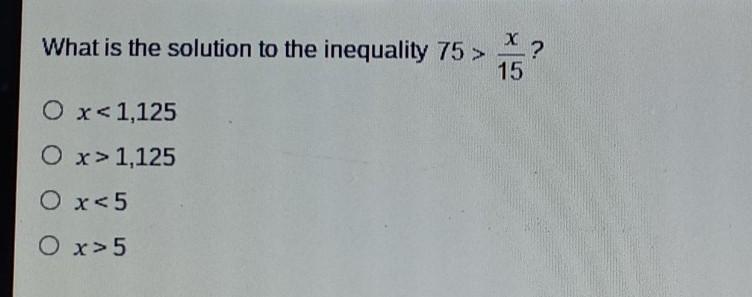
Answers
Answer:
A x<1125
Step-by-step explanation:
Which of the following are necessary to describe a rotation of a figure on a coordinate plane? choose all that apply.
a. the center of rotation.
b. the shape of the figure.
c. the number of degrees of the rotation.
d. the direction of the rotation.
Answers
The necessary components to describe a rotation on a coordinate plane include the center of rotation, the shape of the figure, and the number of degrees of rotation.
To describe a rotation of a figure on a coordinate plane, the necessary components include the center of rotation, the shape of the figure, and the number of degrees of rotation.
a. The center of rotation is a fixed point around which the figure rotates. It serves as the anchor for the rotation and determines the position of the figure after the rotation is applied.
b. The shape of the figure refers to its size, proportions, and geometric characteristics. This information is crucial as the figure retains its original shape during the rotation.
c. The number of degrees of rotation determines the magnitude of the rotation. It specifies how much the figure is rotated around the center of rotation. Positive angles indicate counterclockwise rotations, while negative angles represent clockwise rotations.
d. The direction of rotation is not necessary to describe a rotation on a coordinate plane. The rotation can be defined solely by the center, shape, and angle of rotation.
In summary, the essential components to describe a rotation on a coordinate plane include the center of rotation, the shape of the figure, and the number of degrees of rotation. The direction of rotation is not required to define the rotation.
To know more about coordinate plane, refer here:
https://brainly.com/question/28471473#
#SPJ11
Solve for xxx. Enter the solutions from least to greatest. 3x^2 - 9x - 12 = 03x
2
−9x−12=0
Answers
The solutions to the equation 3x^2 - 9x - 12 = 0 are x = 4 and x = -1.
To solve the quadratic equation 3x^2 - 9x - 12 = 0, we can use the quadratic formula:
x = (-b ± √(b^2 - 4ac)) / (2a),
where a, b, and c are the coefficients of the quadratic equation.
In this case, a = 3, b = -9, and c = -12. Substituting these values into the quadratic formula, we have:
x = (-(-9) ± √((-9)^2 - 4 * 3 * (-12))) / (2 * 3)
= (9 ± √(81 + 144)) / 6
= (9 ± √(225)) / 6
= (9 ± 15) / 6.
We have two possible solutions:
For the positive root:
x = (9 + 15) / 6
= 24 / 6
= 4.
For the negative root:
x = (9 - 15) / 6
= -6 / 6
= -1.
The solutions to the equation 3x^2 - 9x - 12 = 0 are x = 4 and x = -1.
for such more question on equation
https://brainly.com/question/17145398
#SPJ8
Question 3 The Schwarzschild metric is given by 2M 2M ds² -(₁-²M) di² + (1-²¹)- 1- dr² +r² (d0² + sin² 0 dó²). There are Killing vectors associated with time invariance and angular momen- tum invariance in the direction in this geometry leading to the conserved quantities e = (1-2) and l= r² sin² 0 dr From this one can derive an analog to the radial energy equation in Newtonian mechanics by orienting the coordinates so that the orbits are confined to the equatorial plane where 0 = π/2 and u = 0. One finds 2 1 dr + Veff (r) = E 2 dr (e²_ -1) where E = and Veft(r) = - + 2/²/²2 - Mp³². Further, for circular orbits one can show that M | [₁ + √/₁−12 (+1)]. r+= | 2M Finally, for circular orbits of radius R do 1/2 M dt R³ (a) Which value of r corresponds to the Schwarzschild radius of stable circular orbits: r or r? Justify your answer. [3 marks] (b) Show that for circular orbits of radius R do 1/2 M -1/2 3M (²) ¹² (1-³) dT R³ R where is the proper time. [6 marks] (c) A free particle is moving in a circular orbit around a spherical source of curvature of mass M. The Schwarzschild radius of the orbit is 8M. Use the equivalence principle to argue that the period as measured at infinity should be larger than that measured by the particle. [4 marks] (d) Find the period of the orbit as measured by an observer at infinity. Find the period of the orbit as measured by the particle. [7 marks] M
Answers
(A) Circular orbits of stable particles are possible at radii greater than three times the Schwarzschild radius for the non-rotating spherically symmetric mass.
This represents the radius of a black hole's event horizon, within which nothing can escape. The Schwarzschild radius is the event horizon radius of a black hole with mass M.
M can be calculated using the formula: r+ = 2Mwhere r+ is the radius of the event horizon.
(B) 1/2 M -1/2 3M (²) ¹² (1-³) dT = R³ R. This is the required expression.
Tau is the proper time of the particle moving around a circular orbit. Hence, by making use of the formula given above:1/2 M -1/2 3M (²) ¹² (1-³) dT = R³ dt.
(C) Time passes differently in different gravitational fields, and it follows that the period as measured at infinity should be larger than that measured by the particle.
The principle of equivalence can be defined as the connection between gravitational forces and the forces we observe in non-inertial frames of reference. It's basically the idea that an accelerating reference frame feels identical to a gravitational force.
(D) The period of the orbit as measured by an observer at infinity is 16π M^(1/2) and the period of the orbit as measured by the particle is 16π M^(1/2)(1 + 9/64 M²).
The period of orbit as measured by an observer at infinity can be calculated using the formula: T = 2π R³/2/√(M). Substitute the given values in the above formula: T = 2π (8M)³/2/√(M)= 16π M^(1/2).The period of the orbit as measured by the particle can be calculated using the formula: T = 2π R/√(1-3M/R).
Substitute the given values in the above formula: T = 2π (8M)/√(1-3M/(8M))= 16π M^(1/2)(1 + 9/64 M²).
To know more about Schwarzschild radius
https://brainly.com/question/29534114
#SPJ11
Can someone help me with this math homework please!

Answers
Answer:
3. The number of students that rode on each bus
Step-by-step explanation:
The equation they give us is:
2b + 6 = 70
The question already tells us that in this equation:
2 is the 2 buses that the school hired
6 is the 6 leftover kids who couldn't fit on the 2 buses
The question also tells us that the 2 buses only have a total of 64 seats, so 32 seats on 1 bus (64/2 = 32).
So that means b would equal the 32 seats on 1 bus, or the number of students that rode on each bus.
Hope it helps (●'◡'●)
A bill can pass in the U.S. senate with a three-fifths vote. If there are 100 senators, how many are needed to pass a bill?
Answers
Answer:
60
Step-by-step explanation:
3/5 x 100
0.6 x 100
60
Brainliest Appreciated!
Answer quickly pls. 15 points.

Answers
Answer:
56
Step-by-step explanation:
Answer:
The equation for the given equation will be
\(y = 8\)
Step-by-step explanation:
If you have any questions tag on comments
Hope it helps!!!
Tickets to a museum cost $17 each. For a field trip, the museum offer a $4 discount on each ticket. How much will tickets cost for 32 students cost?
Answers
Answer: 416
Step-by-step explanation:
Answer:
416
Step-by-step explanation: the tickets cost 17 each and there is a discount of $4 for a field trip so for that you do 17 minus 4 and you get 13 and then you will multiply 13 by 32 students and you get 416.
I hope this helps!!
How do I do this ?
Because I need help on how to do this correctly

Answers
Answer: 6ft per second
Step-by-step explanation: Its 18ft per 3 seconds. 6x3=18.
Let x and y be real numbers such that x < 2y. Prove that if
7xy ⤠3x2 + 2y2, then 3x ⤠y.
Answers
To prove that 3x ≤ y, assume the opposite, that is, 3x > y, rearrange the inequality substitute x < 2y and simplify, contradict the given condition that x < 2y, therefore, concluding that 3x ≤ y.
Start by assuming the opposite, that is, 3x > y.
From the given inequality,\(7xy \leq 3x^2 + 2y^2,\), we can rearrange to get:
\(7xy - 3x^2 \leq 2y^2\)
We can substitute \(x < 2y\) into this inequality:
\(7(2y)x - 3(2y)^2 \leq 2y^2\)
Simplifying, we get:
\(y(14x - 12y) \leq 0\)
Since y is a real number, this means that either y ≤ 0 or 14x - 12y ≤ 0.
If y ≤ 0, then 3x ≤ y is trivially true.
If 14x - 12y ≤ 0, then we can rearrange to get:
3x ≤ (12/14)y
3x ≤ (6/7)y
3x < y (since we assumed 3x > y)
But this contradicts the given condition that x < 2y, so our assumption that 3x > y must be false.
Therefore, we can conclude that 3x ≤ y.
Know more about inequality here:
https://brainly.com/question/25275758
#SPJ11
Erica chops wood in the forest. The table compares the number of cans of insect repellent Erica uses and the number of mosquito bites she gets each day. Can the number of mosquito bites be represented as a function of the amount of repellent used? Cans of repellent Mosquito bites 0 00 11 1111 1 11 8 88 5 55 2 22 4 44 5 55 2 22 9 99 4 44 5 55 3 33 6 66 2 22 9 9
Answers
Answer:
Step-by-step explanation:
Step-by-step explanation:
Let x represents the number of cans of repellent and y represents the number of mosquitos,
If f be the relation from x to y,
Then by the given table,
f(x) = { (0, 11), (1, 8), (5, 2), (4,5), (2, 9), (3, 6)}
∵ If for each input in a relation has exactly one output, the relation is called a function.
Here, for each value of x there is exactly one value of y,
Hence, f(x) is a relation from x to y,
What is the domain?
What is the range?

Answers
Answer:
domain = -3 \(\leq\) x \(\leq\) 3
range = 2 \(\leq\) x \(\leq\) 1
Step-by-step explanation:
remember, the domain is the input
and the range is the output
so in this case the domain would be the x values, and the range the y values
the x values are
-3 \(\leq\) x \(\leq\) 3
the y values are
2 \(\leq\) x \(\leq\) 1
How many strings of length 8 are there, using digits in {0, 1, 2, 3, 4, 5}, where 6th, 7th, and 8th digits
are distinct, and the difference between the first and second digits is congruent to ±1 (mod 6)?
Answers
To solve this problem we need to use the technique of Counting principle for the total number of strings of length 8 using digits 0, 1, 2, 3, 4, 5.
And, to create strings, we can start with the second character because the first character must follow a certain pattern. Then, after the second character has been chosen, the third, fourth, and fifth characters can be chosen in any order because they are unrestricted. Finally, the last three characters can be selected by specifying that the last two characters are different from the sixth and seventh characters, respectively.
The difference between the first and second digits is congruent to ±1 (mod 6), meaning that the second digit can be 1, 2, or 5 if the first digit is 0. If the first digit is 1, the second digit can be 0, 2, or 3, and so on. Therefore, the first two digits of the string can be chosen in\($3 \times 2 = 6$ ways.\)
Next, we must consider the third, fourth, and fifth digits of the string, which are unrestricted. Each of these digits can be chosen from one of six possible values, resulting in \($6 \times 6 \times 6 = 216$\) possible strings of length 8 with the first five digits.The final three digits of the string must be chosen such that the sixth, seventh, and eighth digits are distinct, and this can be done in\($5 \times 4 \times 3 = 60$ ways.\)
The total number of strings of length 8 is given by the product of the number of ways to choose each of the three groups of digits:\($6 \times 216 \times 60 = 77760$\)
To know more about Counting principle visit:
https://brainly.com/question/29594564
#SPJ11
Select the correct answer. What is the solution to the equation? A. -3 B. 6 C. 7 D. 25
Answers
Answer:
The value of x is 7 if the equation can be reduced to (x + 9)³ = 4096 after applying the properties of the integer exponent option (C) 7 is correct.
What is an integer exponent?
In mathematics, integer exponents are exponents that should be integers. It may be a positive or negative number. In this situation, the positive integer exponents determine the number of times the base number should be multiplied by itself.
It is given that:
The equation is:
After solving:
(x + 9)³ = 4096
x + 9 = ∛4096
x + 9 = 16
x = 7
Thus, the value of x is 7 if the equation can be reduced to (x + 9)³ = 4096 after applying the properties of the integer exponent option (C) 7 is correct.
Find the approximate side length of a square game board with an area of 145 in 2 Plz help!
Answers
Answer:
Side length ≈ 12.04
Step-by-step explanation:
145 = x²
144 is the closest square, with the root 12
The square root of 145 is approximately 12.04
If my answer is incorrect, pls correct me!
If you like my answer and explanation, mark me as brainliest!
-Chetan K
Answer:
The approximate side length is 12.0 in
Step-by-step explanation:
The area of a square is given by
A = s^2 where s is the side length
145 = s^2
Taking the square root of each side
sqrt(145) = sqrt(s^2)
12.04159458 = s
The approximate side length is 12.0 in
The table represents the linear function f(x), and the equation represents the linear function g(x).
Compare the y-intercepts and slopes of the linear functions f(x) and g(x) and choose the answer that best describes them.
x f(x)
01
24
47
g(x) = 2x + 1
A)
The slope of f(x) is less than the slope of g(x). The y-intercept of f(x) is equal to the y-intercept of g(x).
B)
The slope of f(x) is greater than the slope of g(x). The y-intercept of f(x) is equal to the y-intercept of g(x).
C)
The slope of f(x) is less than the slope of g(x). The y-intercept of f(x) is greater than the y-intercept of g(x).
D)
The slope of f(x) is greater than the slope of g(x). The y-intercept of f(x) is greater than the y-intercept of g(x).
Answers
Answer: Based on the given information and the analysis provided, none of the options A, B, C, or D accurately describe the comparison between the y-intercepts and slopes of f(x) and g(x).
Step-by-step explanation:
To compare the y-intercepts and slopes of the linear functions f(x) and g(x), we need to examine the given table for f(x) and the equation g(x) = 2x + 1.
The y-intercept of a linear function represents the point where the graph of the function intersects the y-axis (when x = 0). In the table for f(x), the y-intercept is the value of f(0). However, since the table for f(x) is not provided, we cannot determine the y-intercept of f(x) based on the given information.
The slope of a linear function represents the rate of change of the function. For the linear function g(x) = 2x + 1, the slope is 2. This means that for every unit increase in x, the corresponding y-value increases by 2.
Based on the information provided, we can conclude that the slope of f(x) is not determined, so we cannot compare it to the slope of g(x) accurately. Therefore, none of the given answer options accurately describe the comparison between the y-intercepts and slopes of f(x) and g(x).
It's important to note that without additional information, we cannot determine the exact relationship between the y-intercepts and slopes of f(x) and g(x).
The y-intercept for f(x) and g(x) is the same, and the slope of f(x) is less than the slope of g(x). Therefore, the correct answer is choice A.
Explanation:The y-intercept is the y-value of the function when x equals zero. Looking at the table for f(x), when x equals zero f(x) equals 1, so the y-intercept for f(x) is 1, same to g(x) which also is 1. This makes choice C and D incorrect.
Next, we calculate the slope of each function. The slope is represented by the change in y over the change in x, this can be represented by the formula (delta_y/delta_x). For g(x), in its equation form of y=mx+b, m, the coefficient next to x represents its slope, so its slope is 2. Looking at f(x), we can use the given two points to calculate the slope. Consider the points (0,1) and (2,4), (delta_y/delta_x) equals (4-1)/(2-0)=1.5,which is less than the slope of g(x). So, the slope of f(x) is less than the slope of g(x). This makes the answer choice A.
Learn more about Linear Functions here:https://brainly.com/question/31353350
#SPJ2
Solve this problem I'm confused
3y-9x=27
Answers
So in this case y=3x+9
\( - 9x + 3y - 27 = 0 \\ a = - 9 \\ b = 3 \\ c = 0 \\ {b}^{2} - 4ac = 9 - 4( - 9)( - 27) = 0 \\ x = \frac{ - b}{2a} = \frac{ - 3}{ - 18} = \frac{1}{6} \\ x = \frac{1}{6} \\ y = ( - 9 \times \frac{1}{6} ) + 3y = 27 \\ \frac{ - 3}{2} + 3y = 27 \\ 3y = 27 + \frac{3}{2 } \\ 3y = \frac{57}{2} \\ y = \frac{57}{6} = \frac{19}{2} \\ \)
i hope it helps u.....
What are the solutions to the equation (2x+1)^2-(x+13)=3x^2-2x+2
Answers
4x^2+3x-12=3x^2-2x+2
X^2+5x-14=0
Then use quadratic equation to find the values of the 2 x and you will get,
x=2 and x=-7
What is 8/9 of 360 degree ?

Answers
Answer:
320 degrees.
Step-by-step explanation:
The number of seats in the first row of the
stage left section of the Ming-Sun Theater is
9. As with the center section, the number of
seats in each succeeding row is 2 more than
the row in front of it. How many seats are in
the twenty-fifth row of the stage left section?
Answers
The number of the seats within the 25th row is 227.
According to the statement
We have to seek out that the quantity of seats are within the twenty-fifth row of the left section.
So, For this purpose, we all know that the
According to the information:
The number of seats within the first row of the left section of the Ming-Sun Theater is 9.
As with the middle section, the amount of seats in each succeeding row is 2 over the row ahead of it.
From this information, the equation become to search out the seats is:
Number of seats within the given row(x) = 9x+2
And the number of seats is: Number of seats within the 25th row(25) = 9(25)+2
Number of seats within the 25th row(25) = 225+2
Number of seats within the 25th row(25) = 227.
So, The amount of the seats within the 25th row is 227.
Learn more about succeeding row here
https://brainly.com/question/13763238
#SPJ9
The double number line below shows the approximate number of kilograms in a certain number of pounds:
Two number lines are shown one above the other. The number line on the top shows three longer vertical lines. Between each longer vertical line there is a shorter vertical line. There is one shorter vertical line after the last longer vertical line, thereby making a total of three shorter vertical lines. The longer vertical lines are labeled 3, 5, 7. On the right of this number line is written Pounds. The number line below it also has three longer vertical lines and three shorter vertical lines. The first longer vertical line is ahead of the first longer vertical line of the top number line so that the first shorter vertical line on the lower number line is aligned with the first longer vertical line, labeled 3 on the top number line. The second longer vertical line is ahead of the second longer vertical line of the top number line so that the second shorter vertical line on the lower number line is aligned with the second longer vertical line, labeled 5, on the top number line. The third longer vertical line is ahead of the third longer vertical line of the top number line so that the third shorter vertical line on the lower number line is aligned with the third longer vertical line, labeled 7, on the top number line. The longer vertical lines on the bottom number line are labeled 1, 2, 3, respectively. On the right of this number line is written Kilograms.
Based on the number line, about how many kilograms are there in 9 pounds?
3.50
4.00
4.50
5.00
PLEASE HELP!!!!!!!!! ANSWER ASAP!!!!!!! ITS DUE IN 30 MINUTES!!!!!
WILL MARK BRIANLIEST!!!!!!!!
Answers
PLZ HELP ASAP, IT'S TIMED!!!
Which of the following equations has the given solution set?
Solution set: ∅
-2m + 5 = -2m + 5
-2m + 5 = 2m + 5
-2m + 5 = -2m - 5
Answers
Answer:
what are the options for the selection
A fan blade rotates with angular velocity given by ωz(t)= γ − β
t2.
Part C If y = 4.65 rad/s and ß= 0.835 rad/s³, calculate the average angular acceleration Cav-z for the time interval t = 0 to t = 3.00 s. Express your answer in radians per second squared. 15| ΑΣ�
Answers
Average angular acceleration Cav-z for the time interval t = 0 to t = 3.00 s is -0.2266 rad/s².
Given data:ωz(t) = γ - βt² = -βt² + γWhere, β = 0.835 rad/s³y = ωz(t) = 4.65 rad/s
To find:Average angular acceleration Cav-z for the time interval t = 0 to t = 3.00 s.
Average acceleration formula is given as:Cav-z = Δω/Δt
We can calculate Δω as follows:Δω = ωf - ωi
Where,ωf = final angular velocityωi = initial angular velocity
Since the time interval is given from t = 0 to t = 3 s, initial angular velocity is:ωi = ωz(0) = γ = constant = 5.33 rad/s
Final angular velocity is given as:ωf = ωz(t) = 4.65 rad/sΔω = ωf - ωi = 4.65 - 5.33 = -0.68 rad/s
Now, we can calculate Δt = 3 - 0 = 3 s
Therefore, the average angular acceleration Cav-z is:Cav-z = Δω/Δt= -0.68/3= -0.2266 rad/s²
Answer:Average angular acceleration Cav-z for the time interval t = 0 to t = 3.00 s is -0.2266 rad/s².
Know more about angular acceleration here,
https://brainly.com/question/30237820
#SPJ11
f(x,y)=x³-12x+y³ +3y²-9y Ans: Max (-2,-3); Saddle point (2,-3) and (-2,1); Min (2,1)
Answers
The function F(x, y) has a local maximum at (-2, -3), saddle points at (2, -3) and (-2, 1), and a local minimum at (2, 1).
To find the critical points and classify them as local maxima, local minima, or saddle points, we need to find the partial derivatives of the function F(x, y) and evaluate them at each critical point.
Given the function F(x, y) = x³ - 12x + y³ + 3y² - 9y, let's find the partial derivatives:
∂F/∂x = 3x² - 12
∂F/∂y = 3y² + 6y - 9
To find the critical points, we set both partial derivatives equal to zero and solve the resulting system of equations:
3x² - 12 = 0 --> x² = 4 --> x = ±2
3y² + 6y - 9 = 0 --> y² + 2y - 3 = 0 --> (y + 3)(y - 1) = 0 --> y = -3 or y = 1
Therefore, the critical points are (-2, -3), (2, -3), and (-2, 1).
To classify these critical points, we use the second partial derivatives test. The second partial derivatives are:
∂²F/∂x² = 6x
∂²F/∂y² = 6y + 6
Now, let's evaluate the second partial derivatives at each critical point:
At (-2, -3):
∂²F/∂x² = 6(-2) = -12 (negative)
∂²F/∂y² = 6(-3) + 6 = -12 (negative)
Since both second partial derivatives are negative, the point (-2, -3) corresponds to a local maximum.
At (2, -3):
∂²F/∂x² = 6(2) = 12 (positive)
∂²F/∂y² = 6(-3) + 6 = -12 (negative)
Since the second partial derivative with respect to x is positive and the second partial derivative with respect to y is negative, the point (2, -3) corresponds to a saddle point.
At (-2, 1):
∂²F/∂x² = 6(-2) = -12 (negative)
∂²F/∂y² = 6(1) + 6 = 12 (positive)
Since the second partial derivative with respect to x is negative and the second partial derivative with respect to y is positive, the point (-2, 1) corresponds to a saddle point.
Therefore, the critical points are classified as follows:
Local maximum: (-2, -3)
Saddle points: (2, -3) and (-2, 1)
Local minimum: (2, 1)
Learn more about function here:
https://brainly.com/question/30721594
#SPJ11
bcnf decomposition guarantees that we can still verify all original fd's without needing to perform joins. true false
Answers
True. BCNF (Boyce-Codd Normal Form) decomposition guarantees that we can still verify all original functional dependencies (FDs) without needing to perform joins.
BCNF decomposition ensures that the resulting relations have no non-trivial FDs that violate BCNF, which means all FDs in the original relation are preserved in the decomposed relations. Therefore, we can still verify all original FDs in the decomposed relations without the need to perform joins.
The statement "BCNF decomposition guarantees that we can still verify all original FDs without needing to perform joins" is true. BCNF (Boyce-Codd Normal Form) decomposition ensures the preservation of all original functional dependencies (FDs) without requiring additional join operations.
To know more about BCNF visit:
https://brainly.com/question/31482377
#SPJ11
Factorise completely
qn: 12axy + 8bxy + 4xy
Answers
Answer:
Step-by-step explanation:

Answer:
4xy(3a+2b+1)
Step-by-step explanation:
1) Find the Greatest Common Factor (GCF).
1 - What is the largest number that divides evenly into 12axy, 8bxy and 4xy?
It is 4.
2 - What is the highest degree of \(a\) that divides evenly into 12axy, 8bxy and 4xy?
It is 1, since a is not in every term.
3 - What is the highest degree of \(x\) that divides evenly into 12axy, 8bxy and 4xy?
It is x.
4 - What is the highest degree of \(y\) that divides evenly into 12axy, 8bxy and 4xy?
It is y.
5 - What is the highest degree of \(b\) that divides evenly into 12axy, 8bxy and 4xy?
It is 1, since \(b\) is not in every term.
6 - Multiplying the results above,
GCF = 4xy
2) Factor out the GCF. (Write the GCF first. Then, in parentheses, divide each term by the GCF.)
\(4xy(\frac{12axy}{4xy} +\frac{8bxy}{4xy} +\frac{4xy}{4xy} )\)
3) Simplify each term in parentheses.
\(4xy(3a+2b+1)\)
PLEASE HELP!!!
Solve for x using the Quadratic Formula: x2 + 2x + 1 = 0
-b+Vb2-4ac
X=
2a
Ox=2
Ox= 1
O x = 0
O x = -1

Answers
Answer:
last option, x = -1
Step-by-step explanation:
\(x^{2} + 2x + 1 = 0\\x_{1} = \frac{-2 + \sqrt{2^{2} - 4(1)(1) } }{2(1)}\\x_{2} = \frac{-2 - \sqrt{2^{2} - 4(1)(1) } }{2(1)}\\x_{1} = \frac{-2 + \sqrt{0} }{2}\\x_{2} = \frac{-2 - \sqrt{0} }{2}\\x = \frac{-2}{2} \\x = -1\)
The value of x by using the Quadratic Formula is,
⇒ x = - 1
What is Quadratic equation?An algebraic equation with the second degree of the variable is called an Quadratic equation.
Given that;
Equation is,
⇒ x² + 2x + 1
Now, We can use the Quadratic Formula for x as;
⇒ x² + 2x + 1
⇒ x = - 2 ± √2² - 4×1×1 / 2
⇒ x = - 2 ± √4 - 4 / 2
⇒ x = - 2 / 2
⇒ x = - 1
Thus, The value of x by using the Quadratic Formula is,
⇒ x = - 1
Learn more about the quadratic equation visit:
brainly.com/question/1214333
#SPJ5