A company is moving large equipment in the boxes in the shape of cubes that holds 2000 ft.³ the company needs to move the boxes by placing them on square platforms the square base of the cube must entirely say on the square platform the Square platforms have side lengths that only come in whole foot lengths What is the smallest whole foot length that could be used for the square platforms
Answers
Answer:
Step-by-step explanation:
Volume of a cube = L³
L is the length of the side of the cube;
Given
L = 2000ft³
Required
smallest whole foot length that could be used for the square platforms
Substitute the given into the formula to get the unknown length L
2000 = L³
Rearrange
L³ = 2000
Take cube root of both sides
∛L³ = ∛2000
L = ∛2000
L = 12.599
L≈ 12.6 feet
Hence the smallest whole foot length that could be used for the square platforms is 12.6feet
Related Questions
Please solve with explanation (High Points)

Answers
The equation of the transformed function is f(x)= -1/3\(\sqrt{2(x-6)}\) -3.
Given that,
The f(x) = square root of X base function is transformed by a reflection in the x-axis, a vertical stretch by a factor of 3, a horizontal compression by a factor of 1/2, a vertical translation by a factor of 3, a vertical translation by a factor of 3 down, and then a horizontal translation by a factor of 6 right.
We have to verify the changed function's equation.
Take the function
f(x)=√x
The function reflection in the x-axis,
f(x)=-√x
The function is vertical stretch by a factor of 3.
f(x)= -1/3√x
The function is horizontal compression by a factor of 1/2.
f(x)= -1/3\(\sqrt{2x}\)
The function is vertical translation by a factor of 3 down,
f(x)= -1/3\(\sqrt{2x}\) -3
The function is horizontal translation by a factor of 6 right.
f(x)= -1/3\(\sqrt{2(x-6)}\) -3
Therefore, The equation of the transformed function is f(x)= -1/3\(\sqrt{2(x-6)}\) -3.
To learn more about function visit: https://brainly.com/question/21145944
#SPJ1
how to solve step by step 4(x-7)=-6x+12
Answers
Answer:
x = 3
Step-by-step explanation:
4 ( x - 7 ) = -6x + 12
→ Expand brackets
4x - 28 = -6x + 12
→ Add 6x to both sides
10x - 28 = 12
→ Add 28 to both sides
10x = 30
→ Divide both sides by 10
x = 3
Determine the area under the standard normal curve that lies between â(a) Upper Z equals negative 0.12Z=â0.12 and Upper Z equals 0.12Z=0.12â, â(b) Upper Z equals negative 0.35Z=â0.35 and Upper Z equals 0Z=0â, and â(c) Upper Z equals 0.02Z=0.02 and Upper Z equals 0.82Z=0.82. â(a) The area that lies between Upper Z equals negative 0.12Z=â0.12 and Upper Z equals 0.12Z=0.12 is nothing. â(Round to four decimal places asâ needed.) â(b) The area that lies between Upper Z equals negative 0.35Z=â0.35 and Upper Z equals 0Z=0 is nothing. â(Round to four decimal places asâ needed.) â(c) The area that lies between Upper Z equals 0.02Z=0.02 and Upper Z equals 0.82Z=0.82 is nothing
Answers
Answer:
The answer is below
Step-by-step explanation:
The z score is a measure used in statistic to determine the number of standard deviations by which the raw score is above or below the mean. . The z score is given by:
\(z=\frac{x-\mu}{\sigma}\\ where\ \mu \ is \ the\ mean, \sigma\ is\ the\ standard\ deviation\ and\ x \ is\ the\ raw\ score\)
(a) Z = -0.12 and Z = 0.12
From the normal distribution table, Area between z equal -0.12 and z equal 0.12 = P(-0.12 < z < 0.12) = P(z < 0.12) - P(z < -0.12) = 0.5478 - 0.4522 = 0.0956 = 9.56%
b) The area that lies between Z = - 0.35 and Z=0
From the normal distribution table, Area between z equal -0.35 and z equal 0 = P(-0.35 < z < 0) = P(z < 0) - P(z < -0.35) = 0.5 - 0.3594 = 0.1406 = 14.06%
c) The area that lies between Z = 0.02 and Z = 0.82
From the normal distribution table, Area between z equal 0.02 and z equal 0.82 = P(0.02 < z < 0.82) = P(z < 0.82) - P(z < 0.02) = 0.7939 - 0.5080 = 0.2859 = 28.59%
1)Calculate the gradient between 1,4 and 4,19.
2)Calculate the gradient between 3,9
5,5
3)Calculate the gradient between -3,4 and -1, 18
Answers
1. the gradient between (1,4) and (4,19) is:
(19 - 4) / (4 - 1) = 15 / 3 = 5
2. The gradient between (3,9) and (5,5) is:
(5 - 9) / (5 - 3) = -4 / 2 = -2
3. The gradient between (-3,4) and (-1,18) is:
(18 - 4) / (-1 + 3) = 14 / 2 = 7
A figure has vertices (−13, 13),(26, 52), (39, 39). What would be the new coordinates of the vertices to the nearest tenth if the image were reduced by a scale factor of 0.77 with the origin as the center of dilation?
A. −16.9, 16.9), (33.8, 67.6), (50.7, 50.7)
B. (−10, 10), (20, 40), (30, 30)
C. (10, 10), (−20, 40), (−30, 30)
D. (16.9, 16.9), (33.8, 67.6), (50.7, 50.7)
Answers
The new coordinates after a reduced scale factor of 0.77 with the origin will be equal to (−10, 10), (20, 40), (30, 30). Hence, option B is correct.
What is a graph?In math, graph science is the theory of geometric structures called graphs that are used to represent pairwise different objects. Vertices—also known as nodes or points—that are joined by edges make form a network in this sense.
Undirected graphs, where edges connect two vertices equally, and focused therapy, where edges connect two vertices unevenly, are distinguished.
As per the data given in the question,
We will combine the x and y dimensions even by scale factors to shrink the picture by a multiplier of 0.77 with both the origins as that of the center of dilatation because the figure's vertices are (-13, 13), (26, 52), and (39, 39).
So, the first point is (-13, 13)
-13 × 0.77 = -10 and,
13 × 0.77 = 10
So, the new point is (-10, 10).
The second point is (26, 52).
26 × 0.77 = 20
52 × 0.77 = 40
So, the new point is (20, 40)
The third point is (39, 39)
39 × 0.77 = 30
39 × 0.77 = 30
So, the new point is (30, 30).
To know more about Graph:
https://brainly.com/question/17267403
#SPJ1
John spent 80% of his money and saved the rest. Peter spent 75% of his money and saved the rest. If they saved the same amount of money, what is the ratio of John’s money to Peter’s money? Express your answer in its simplest form.
Answers
The ratio of John's money to Peter's money is 5/4. This means if John has a total amount of 5 then Peter will have a total of 4 as his amount.
Let's assume John has 'x' amount of money, Peter has 'y' amount of money, The money John saved is 'p' and the money Peter saved is 'q'
So,
p = x - 80x/100 (equation 1)
q = y - 75y/100 (equation 2)
According to the given question, the amount John saved is equal to the amount Peter saved. Hence, we can equate equations 1 and 2.
p = q
x- 80x/100 = y - 75y/100
x - 0.8x = y - 0.75y
0.2x = 0.25y
x = 0.25y/0.2
x/y = 0.25/0.2
x/y = 25/20
x/y = 5/4
Hence, the ratio of John's money to Peter's money is 5/4.
To learn more about Ratio:
https://brainly.com/question/13419413
A group of 23 friends are at the theater but can't agree on which movie to see. some of the group decides to see lightyear which is playing for $4 per ticket and the rest of the group decides to see jurassic park which is playing for $9 per ticket. altogether the group spends $172, how many of them saw lightyear?
Answers
The number of people who watched light year are 7.
Let x= number of friends that watches light year
and y= number of friends that watches jurassic park.
Let the equations be
All together total cost => 4x+9y=172 ------> 1
And total number of people=> x + y=23 ------> 2
By multiplying both equations by 1 and 4 respectively we can get,
By Solving above two equations we get, x=7 and y=16
As X represents number of friends that watches light year, the answer is 7
Therefore, number of people that watches light year will be 7.
To learn more about light year click here:
brainly.com/question/27046045
#SPJ4
Please answer it now in two minutes

Answers
Answer:
p = 67
Step-by-step explanation:
The polygon has 8 sides.
The sum of the measures of the interior angles is:
180(n - 2) = 180(8 - 2) = 180(6) = 1080
p + 49 + 2p + 7 + 2p + 142 + p + 50 + 2p + 147 + 2p + 15 = 1080
10p + 410 = 1080
10p = 670
p = 67
meredith is a general surgeon who performs surgeries such as appendectomies and laparoscopic cholecystectomies. the average number of sutures that meredith uses to close a patient is 37, and the standard deviation is 8. the distribution of number of sutures is right skewed. random samples of 32 are drawn from meredith's patient population, and the number of sutures used to close each patient is noted. use the central limit theorem to find the mean and standard error of the sampling distribution. select the statement that describes the shape of the sampling distribution. group of answer choices unknown the sampling distribution is normally distributed with a mean of 37 and standard deviation 1.41. the sampling distribution is right skewed with a mean of 37 and standard deviation 8. the sampling distribution is normally distributed with a mean of 37 and standard deviation 8. the sampling distribution is right skewed with a mean of 37 and standard deviation 1.41.
Answers
The statement that accurately describes the form of the sampling distribution is:The inspecting dissemination is regularly circulated with a mean of 37 and standard deviation 1.41.
According to the central limit theorem, regardless of how the population distribution is shaped, the sampling distribution of the sample mean will be approximately normally distributed for a sufficiently large sample size.
For this situation, irregular examples of 32 are drawn from Meredith's patient populace, which fulfills the state of a sufficiently huge example size. The central limit theorem can be used to determine the sampling distribution's mean and standard error.
In this instance, the population mean, which is 37, is equal to the mean of the sampling distribution.
The population standard deviation divided by the square root of the sample size is the sampling distribution's standard error. For this situation, the standard mistake is 8 partitioned by the square foundation of 32, which is around 1.41.
Therefore, the statement that accurately describes the form of the sampling distribution is:
The inspecting dissemination is regularly circulated with a mean of 37 and standard deviation 1.41.
To know more about central limit theorem refer to
https://brainly.com/question/898534
#SPJ11
nine divide by 60?? and nine divided by 390
Answers
When nine is divided by 60 , the quotient would be 0. 15 .
The quotient when nine is divided by 390 is 0. 023 or 3 / 130 .
How to find the quotient ?The quotient refers to the result when a number is divided by another number as is the case with nine being divided by 60 .
The quotient is therefore :
= 9 ÷ 60
= 9 / 60
= 0. 15
The quotient for the division of nine by 390 is :
= 9 ÷ 390
= 9 / 390
= 0. 023
Another way to do this is to find the greatest common factor of nine and 390 which is 3 . Then use it to take the numbers to their simplest form. The quotient would then be :
= ( 9 / 3 ) / ( 390 / 3 )
= 3 / 130
Find out more on division at https://brainly.com/question/14355516
#SPJ1
WILL GIVE BRAINLIEST
y = 2x - 9
y = 1/2x + 3
These two lines are:
parallel
perpendicular
neither
Answers
Answer:
neither
Step-by-step explanation:
Parallel lines have equal slopes
The product of the slopes of perpendicular lines = - 1
The equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
y = 2x - 9 ← is in slope- intercept form
with slope m = 2
y = \(\frac{1}{2}\) x + 3 ← is in slope- intercept form
with slope m = \(\frac{1}{2}\)
2 ≠ \(\frac{1}{2}\) , then lines are not parallel
2 × \(\frac{1}{2}\) = 1 ≠ - 1, then lines are not perpendicular
First one to answer this gets brainlest:
What is 5 * 4 + (6 / [ 2 + 1 ] ) *11
Answers
Answer:
42
Step-by-step explanation:
5 * 4 + (6 / [ 2 + 1 ] ) *11
5 * 4 +2 * 11
20 +2 * 11
20+ 22
42
Answer:
Step-by-step explanation:
5 x 4 + 6/3 x 11
20 + 2 x 11
20 + 22
42
2/5 in Fraction form?
Answers
Answer:
2/5 is fraction form.
0.4 is decimal form btw.
Find the length of BC¯¯¯¯¯¯¯¯
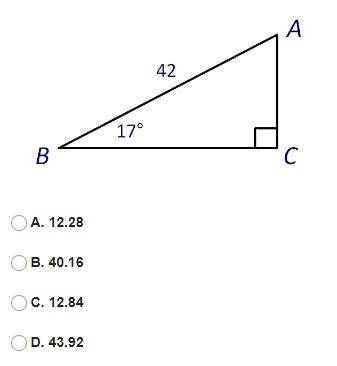
Answers
Answer:
B
Step-by-step explanation:
I love trig lol,
Assuming you know trig, Cos(17)=BC/42
Cos(17)*42=BC
Cos(17)~0.956
0.956*42=40.152=BC
Since this is a approximation, B is the closest to our estimate.
Can someone please help me? It’s due tmrw.
For Exercises 1-3 use the following information. Then estimate to find the distance sound travels through each material in each given time.
Problem: Sound travels through different materials at different speeds. For example, the graph shows that in one second, sound travels 5,971 meters through stone.
However, it travels only 346 meters through air in one second.
1. air, 20 seconds
Answer:??
2. Stone, 12 seconds
Answer:??
3. Estimate how much farther sound travels through stone in 17 seconds than through aluminum in the same time.
Answer:??
Thanks! :)
Chart
|
|
|
|
|
|
\/

Answers
Answer:
Step-by-step explanation:
1. We know it travels 346 meters in a second, we now need to multiply 346 by 20. This equals 6920
2. Sound travels 5971 meters per second. We need to multiply this by 12 to find the distance it travels in 12 seconds. 71652 meters
3. We know sound travels 5971 meters per second in stone and 5000 meters per second from the chart. We need to find the difference between these and multiply that by 17 to find the distance covered in 17 seconds.
5971-5000=971
971*17=16507
Sound travels 16507 more meters in 17 seconds through stone than it would travel in aluminum
At a craft fair, Emily sold paper flowers for $0.55 each. She sold
48 flowers. How much money did she make?
Answers
Answer:
$26.40
Step-by-step explanation:
Answer:
$26.40
Step-by-step explanation:
1 paper flower=$0.55
Therefore,48 paper flowers=?
cross multiplying,we have 0.55×48=$26.40
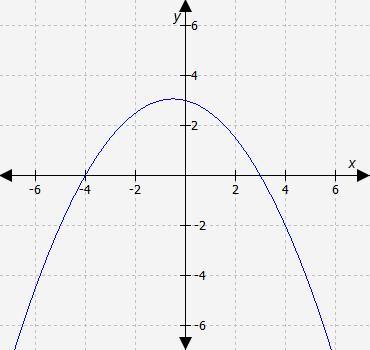
Use the graph of y = -x2 - 2x + 3 to solve
the equation -x2 - 2x + 3 = 0. What are
the solutions?
Answers
y
+
2
x
=
3
y
=
−
2
x
+
3
When
x
=
0
, y-intercept
=
3
coordinates
(
0
,
3
)
When
y
=
0
, x-intercept
=
3
2
coordinates
(
3
2
,
0
)
Knowing two points, we can draw the graph.
graph{-2x + 3 [-10, 10, -5, 5]}
Answer
Select the correct answer. If function f has zeros at -3 and 4, which graph could represent function f?



Answers
Answer:
first one
Step-by-step explanation:
The graph intersects x-axis at (4,0) and (-3,0)
If function f has zeros at -3 and 4 then the first graph represents the function f.
When a function has zeros at -3 and 4, it means that the function's value is equal to zero at those x-values.
In other words, when x = -3 and x = 4, the function f(x) becomes 0.
To represent this on a graph, you should look for two points where the graph intersects the x-axis at -3 and 4.
When the graph crosses the x-axis at these points, it indicates that the function has zeros at those x-values.
When we observe the graphs, the first graph has zeros at -3 and 4.
Hence, the first graph could represent the function f with zeros at -3 and 4.
To learn more on Functions click:
https://brainly.com/question/30721594
#SPJ4
Which of the following describes the graph of flow versus viscositya.As viscosity increased, the flow rate increased and the graph was curvedb.As viscosity increased, the flow rate decreased and the graph was curvedc.As viscosity increased, the flow rate increased and the graph was lineard.As viscosity increased, the flow rate decreased and the graph was linear
Answers
The correct answer is d. As viscosity increased, the flow rate decreased and the graph was linear.
Viscosity is a measure of a fluid's resistance to flow. The higher the viscosity of a fluid, the more resistant it is to flow. Flow rate, on the other hand, is a measure of how much fluid flows through a particular point in a given amount of time.
When viscosity increases, the flow rate decreases, and this relationship is linear. This means that as viscosity increases, the flow rate decreases at a constant rate, resulting in a straight-line graph. The slope of this graph represents the degree of change in flow rate with respect to viscosity.
In contrast, if the flow rate were to increase as viscosity increased, the graph would be curved, indicating a nonlinear relationship between the two variables. Therefore, option d is the correct answer, and the other options do not accurately describe the relationship between flow rate and viscosity.
Learn more about graph here:
https://brainly.com/question/17267403
#SPJ11
50 POINTS- FIND THE VALUE OF X

Answers
The angle is half the angle of the arc, so 7x+9=46
7x+9=46
7x=37
x=37/7
When testing a right-tailed hypothesis using a significance level of 0.025, a sample size of n=13, and with the population standard deviation unknown, what is the critical value? H0: u≥2 hours and H1:u<2 hours H0:u<2 hours and H1:u≥2 hours H0:u=2 hours and H1:u=2 hours H:u≤2 hours and H1:u>2 hours
Answers
The correct answer is a. H0: u≥2 hours and H1:u<2 hours. When testing a right-tailed hypothesis using a significance level of 0.025, a sample size of n=13, and with the population standard deviation unknown, the critical value is as follows:
To determine the critical value, we need to use the t-distribution since the population standard deviation is unknown.
Using a t-distribution table or calculator with 12 degrees of freedom (n-1), a one-tailed test, and a significance level of 0.025, the critical value is 2.1604.
If the test statistic is greater than or equal to this value, we can reject the null hypothesis in favor of the alternative hypothesis, which is a right-tailed hypothesis.
To learn more about right-tailed hypothesis, refer:-
https://brainly.com/question/17199362
#SPJ11
Ben is playing a card game. The numbers of the cards in his hand are 2, 3, 4, 4, 5, 7, 9, and 10. Ben may only play one card at a time.
What is the probability the next card Ben plays will be an odd number?
343 fourths
121 half
383 eighths
14
Answers
Answer: Half
Step-by-step explanation:
Simply describe Bayes rule and give an example of how it may be
used.
Answers
Bayes' rule, also known as Bayes' theorem or Bayes' law, is a mathematical formula used in probability theory and statistics. It provides a way to update our belief or probability of an event occurring, given new evidence.
The formula for Bayes' rule is:
P(A|B) = (P(B|A) * P(A)) / P(B)
where P(A|B) is the probability of event A occurring given that event B has occurred, P(B|A) is the probability of event B occurring given that event A has occurred, P(A) is the prior probability of event A occurring, and P(B) is the prior probability of event B occurring.
An example of how Bayes' rule can be used is in medical diagnosis.
Let's say a patient has a positive test result for a certain disease.
The probability of having the disease (event A) can be calculated using Bayes' rule, taking into account the sensitivity and specificity of the test.
The sensitivity is the probability of a positive test result given that the patient has the disease, and the specificity is the probability of a negative test result given that the patient does not have the disease.
By applying Bayes' rule, we can update the probability of having the disease based on the test result and the sensitivity and specificity values.
In short, Bayes' rule is a useful tool for updating probabilities based on new evidence. It is commonly used in various fields, including medicine, finance, and machine learning.
To know more about mathematical , visit ;
https://brainly.in/question/33520724
#SPJ11
Which inequalities correctly show the relationship between the numbers 13, −4, and −17?
Answers
Answer:
13 > -17 < -4
Step-by-step explanation
13 = postive number
-17 and -4 = negtive.
13 is greater than -17
Since negtive is oppistie of postive it goes backwards.
So -4 is greater than -17
(Im new to this so Im not sure if it is correct)
Suppose you roll a die. What is the probability that you do not roll a 4?

Answers
Answer:
5/6
Step-by-step explanation:
There are six sides on a die, and they are asking the probability of not rolling a 4. So it would be 5 out of 6
Have a good day :)
HELPLSPLSPLPSLPSLPSL

Answers
Answer:
25.5
Step-by-step explanation:
first find the area od the rectangle than the triangle.
to find the area count the number of squares and use A=b*h
than do the same for the triangle using A=.5*b*h
15=3*5
10.5=.5*3*7
10.5+15=25.5
HELP PLS!! What is the diameter of a circle whose circumference is 16pi centimeters?
32 cm
16 cm
4 cm
8 cm

Answers
answer: 8
Explanation:
Use the formula for the area of a circle:
A = π r 2
Here, the area is 16 π
16 π = π r 2
Divide both sides by
16 = r 2
Take the square root of both sides:
√ 16 = √ r 2
4 = r
Since the radius of the circle is
4
, the diameter is twice that:
d = 4 × 2 = 8
Find the period and the amplitude of the periodic function. I'm awful with graphs :(
Answers
A period is the difference in x over which a sine function returns to its equivalent state and the amplitude is A/5.
Amplitude:
The amplitude of a periodic variable is a measure of its change over a period of time, such as a temporal or spatial period. The amplitude of an aperiodic signal is its magnitude compared to a reference value. There are various definitions (see below) of amplitude, which is any function of the magnitude of the difference between the extreme values of a variable. In the previous text, the phase of a periodic function is called the amplitude.
X = A sin (ω[ t - K]) + b
A is the amplitude (or peak amplitude),
x is the oscillating variable,
ω is angular frequency,
t is time,
K and b are arbitrary constants representing time and displacement respectively.
According to the Question:
An equation does not have an amplitude. This "equation" represents the formula of a vibration, and was better written as:
X= A/5* sin(1000.t + 120)
These oscillations have a certain amplitude. X values can vary from minimum to maximum. Normally, the stop position of the oscillation is X=0. In this case, we can see that the maximum occurs when the sine is +1 and the minimum occurs when the sine is -1.
For theses cases X= A/5 respectively -A/5.
Therefore,
The amplitude is A/5.
For formulas of this type, the term in front of the sinus (or cosine) is equal to the amplitude.
Complete question:
Can I find the amplitude of this equation? A/5 *

Cory is reading a graph of equivalent ratios. If 1 of the ratios is represented as 3,5 which could be another ratio
I don’t know if that made sense aaa
Answers
The other ratio equivalent to (3, 5) will be (9, 15).
What is ratio?A ratio is an ordered pair of numbers a and b, written a / b where b does not equal 0. A proportion is an equation in which two ratios are set equal to each other.
Given that, Cory is reading a graph of equivalent ratios. If 1 of the ratios is represented as 3,5 which could be another ratio
In the given options,
a) (6, 8) = 3, 4
b) (8, 6) = 4, 3
c) (9, 15) = 3, 5
Since, (9, 15) = 3, 5
Hence, the equivalent ratio will be (9, 15).
Learn more about ratio, click;
https://brainly.com/question/13419413
#SPJ1

Someone help please thank you show your work 100 points!!

Answers
Answer:
A
Step-by-step explanation:
y=-2 when x=-4 y=-4 when x=-8
what's given: 4. what's given:2
-4k=-2. -8k=-4
-4/4. -2/4. -8/8. -4/8
k=0.5. k =0.5
0.5(2) =1. 0.5(2)=1
Answer:
(a) no; (b) no; (c) yesy=5x; b=1/2a; m = 5nk = 5; x = 9.8Step-by-step explanation:
You want to identify the proportional relations in the given tables and equations, and you want to find and use the constant of variation given that y=35 when x=7.
Proportional relationA proportional relation is one that has an equation of the form ...
y = kx
One variable is a constant multiple of the other. If the relation cannot be put in this form, it is not a proportional relation.
ApplicationThe value of k in the above equation can be found as ...
k = y/x . . . . . . . divide both sides by x
This is a constant if the relation is proportional.
1a.y/x = -8/-4 = -4/-2 ≠ 18/6 . . . . . not a proportional relation
1b.y/x = -4/-5 ≠ 10/2 . . . . . not a proportional relation
1c.y/x = -12/-3 = 24/6 = 32/8 = 4 . . . . . a proportional relation
2.
You are looking for equations of the form y = kx. The only ones having that form are ...
y = 5xb = 1/2am = 5nThe others represent inverse proportions and a linear (not proportional) relation.
3.As we saw above, the constant of variation is ...
k = y/x = 35/7
k = 5
Then the value of x can be found from ...
49 = 5x
49/5 = x = 9.8