a) If volume of a cylinder is 4817 and the radius is 4, find the height.
Answers
Answer:
71. 8
Step-by-step explanation:
volume of a cylinder = 4/ 3 π r² h
=> 4817 = 4/ 3 × 22/ 7 × 4² × h
=> h = (4817 × 3 × 7)/ (4 × 22 × 4²)
=> h = 71.8
Related Questions
NEED HELP ASAP Which is an equivalent expression for (52 • 34)3?
15 18
56 • 312
52 • 312
55 • 37
Answers
The expression that is equivalent to the expression given as (52 • 34)3 is 5^4 • 3^12
How to determine the equivalent expression?The expression is given as:
(52 • 34)3
Rewrite properly as:
(5^2 • 3^4)^3
Expand the expression
(5^2)^2 • (3^4)^3
Evaluate the products of the exponents
(5^4) • (3^12)
Remove the brackets
5^4 • 3^12
Hence, the expression that is equivalent to the expression given as (52 • 34)3 is 5^4 • 3^12
Read more about equivalent expressions at:
https://brainly.com/question/2972832
#SPJ1
Answer:
its 5^6 x 3^12
Each table in a library can seat up to 5 people. There are enough tables for 75 people. How many tables are there in the library?
Answers
Answer:
15 tables
Step-by-step explanation:
75/5 = 15
Answer:
There are 15 tables in the library.
Step-by-step explanation:
You know this because you know the library holds 75 people and you know how many people can sit at a table so to find the answer you divide 75 by 5 and you get 15. To check this you can multiply 15 by 5 and you will get 75.
What is the midpoint of the horizontal line segment graphed below?10(-6,3)(10,3)10A. (2,6)В. (4, 6)ОООC. (2, 3)D. (4, 3)

Answers
Therefore,
(-6, 3)(10, 3)
\(\begin{gathered} (x_m,y_m)=(\frac{-6+10}{2},\frac{3+3}{2}) \\ (x_m,y_m)=(\frac{4}{2},\frac{6}{2}) \\ (x_m,y_m)=(2,3) \end{gathered}\)A baseball pitcher won 20 of the games he pitched last year. If he won 28 ballgames this year, what was his percent of increase?
Answers
Il faut calculer la différence entre les deux nombres, la diviser par l'ancienne valeur, puis multiplier par 100 pour obtenir le pourcentage.
La différence entre les deux nombres est :
28 - 20 = 8
L'ancienne valeur est 20, donc nous avons :
(8 / 20) x 100 = 0.4 x 100 = 40
Le pourcentage d'augmentation est donc de 40%. Le lanceur de baseball a augmenté son nombre de victoires de 40% par rapport à l'année précédente.
Select all the correct answers. the square of a number is 3 less than four times the number. which values could be the number?
Answers
The given expression "the square of a number is 3 less than four times the number" is represented as x² = 3 - 4x and the values of number could be: x1= 0.645 , x2= -4.645
In mathematics, when we refer "square of a number" we mean that the exponent of that number is 2. So we express it mathematically as:
x²
When we express "3 less than" of a number we mean that the number 3 is subtracting that number. So we express it mathematically as: 3 -
x² = 3 -
When we express "four times the number" we mean that the number is exactly 4 times greater than a number or that it contains it 4 times. So we express it mathematically as: 4x
x² = 3 - 4x
Organizing the values, we have a quadratic equation: x² + 4x – 3 = 0
Where:
a= 1b= 4c= -3Solving the quadratic question we get the values for the (x) number
x= {- b ± √ [b² - (4* a*c)]} / (2 *a)
x= {- 4 ± √ [4² - (4* 1*-3)]} / (2 * 1)
x= {- 4 ± √ (16 + 12)} / 2
x= {- 4± √ 28} / 2
x= (- 4 ± 5.29 ) / 2
x1= (- 4 + 5.29 ) / 2
x1= (1,29) / 2
x1= 0.645
x2= (- 4 - 5.29 ) / 2
x2= (9.29) / 2
x2= -4.645
We can check the values, replacing them into the equation:
(x1)² = 3 - 4(x1)
(0.645)² = 3 - 4*(0.645)
0.42 = 0.42
(x2)² = 3 - 4(x2)
(-4.645)² = 3 - 4*(-4.645)
21.58 = 21.58
What is a quadratic equation?It is an algebraic equation where the polynomial formed has three terms, one variable has an exponent 2, another in which the variable has exponent 1 and the last term without any variable. Its standard form is:
ax²+ bx + c = 0
Learn more about quadratic equation at: brainly.com/question/25841119 and brainly.com/question/7784687
#SPJ4
Find the general solution of the following PDE: \[ u_{x x}-2 u_{x y}-3 u_{y y}=0 \]
Answers
We need to find the general solution of the above PDE. Let's solve the above PDE by the method of characteristic. Let us first solve the PDE by using the method of characteristics.
The method of characteristics is a well-known method that provides a solution to the first-order partial differential equations. To use this method, we first need to find the characteristic curves of the given PDE. Thus, the characteristic curves are given by $x = t + c_1$.
Now, we need to eliminate $t$ from the above equations in order to obtain the general solution. By eliminating $t$, we get the general solution as:$$u(x,y) = f(2x - 3y) + 3(x - 2y)$$ where $f$ is an arbitrary function of one variable. Hence, the general solution of the PDE $u_{xx} - 2u_{xy} - 3u_{yy} = 0$ is given by the above equation. Thus, the main answer to the given question is $u(x,y) = f(2x - 3y) + 3(x - 2y)$. In order to find the general solution of the PDE $u_{xx} - 2u_{xy} - 3u_{yy} = 0$, we first used the method of characteristics. The method of characteristics is a well-known method that provides a solution to the first-order partial differential equations.
To know more about solution visit:
https://brainly.com/question/1616939
#SPJ11
Write the equation in standard form for the circle with center (3,0) and radius 5.
Answers
The equatiοn οf the circle will be \(x^{2}+y^{2} -6x-16=0\)
What is circle?A clοsed rοund shaped figure which cοntains nο cοrners is called circle. It has center called (h, k) and radius r. Rοund clοck, car tire, wheels are the examples οf circle.
If the center and radius is given then the equatiοn οf circle is:
\((x-h)^{2} + (y-k)^{2} = r^{2}\) ------------- (1) where (h, k) centre and r radius.
Here center οf the circle is (3,0) and radius οf the circle is 5
putting h= 3 , y=0 and r=5 in equatiοn (1) we get
\((x-3)^{2} + (y-0)^{2} =5^{2}\)
⇒ (x²- 6x+9) +y²=25
⇒ x²+y²-6x+9-25=0
⇒x²+y²-6x-16=0
Hence the equatiοn οf circle is x²+y²-6x-16=0.
To learn more about circle
https://brainly.com/question/11833983
#SPJ1
what is the percentage of 28% of n is 196
Answers
Answer:
700
Step-by-step explanation:
28 % of n = 28/100 x n = 0.28n
If 28% of n = 196 that means
0.28n = 196
Divide both sides by 0.28
0.28n/0.28 = 196/0.28
n = 700
what standard deviation is used in scientific?
Answers
The standard deviation used in scientific research is typically the sample standard deviation, also known as the population standard deviation estimator. It is a measure of the dispersion or variability of data points around the mean.
In scientific research, the standard deviation is a commonly used statistical measure that quantifies the spread of data points in a sample or population. It provides information about how much individual data points deviate from the mean. The sample standard deviation is used when working with a sample of data to estimate the population standard deviation.
The formula for calculating the sample standard deviation involves taking the square root of the average of the squared differences between each data point and the mean. It is represented by the symbol "s" and is used to describe the variability or dispersion of data within the sample.
The population standard deviation, represented by the symbol "σ," is used when working with an entire population rather than a sample. However, in scientific research, due to practical limitations, researchers often rely on sample data to make inferences about the larger population. Therefore, the sample standard deviation is commonly used as an estimator for the population standard deviation.
To learn more about standard deviation click here:brainly.com/question/12402189
#SPJ11
let and . find the vector and its additive inverse. , , ,
Answers
The vector u is (2,3,-4) and its additive inverse is (-2,-3,4).
To find the vector u and its additive inverse, we will use the formula for the additive inverse of a vector which is -u = -(x,y,z) = (-x,-y,-z).
Given:
u = (2,3,-4)
To find the additive inverse of u, we will multiply each component by -1:
-u = -(2,3,-4) = (-2,-3,4)
Therefore, the vector u is (2,3,-4) and its additive inverse is (-2,-3,4).
Learn about Vector
brainly.com/question/29740341
#SPJ11
What is the y-intercept (b) and the slope (m) that represents the linear
equation of y = 8x - 5?
Answers
Answer:
y- intercept = - 5, slope = 8
Step-by-step explanation:
The equation of a line in slope- intercept form is
y = mx + b ( m is the slope and b the y- intercept )
y = 8x - 5 ← is in slope- intercept form
with slope m = 8 and y- intercept b = - 5
Answer: slope: 8, intercept: (0, −5)
Step-by-step explanation:
Find the Slope and y-intercept
y = 8x − 5
The slope-intercept form is y = mx + b, where m is the slope and b is the y-intercept.
y = mx + b
Find the values of m and b using the form y = mx + b.
m = 8
b = −5
The slope of the line is the value of m, and the y-intercept is the value of b.
Slope: 8
intercept: (0, −5)

Solve for X and round to the nearest tenth

Answers
Answer:
x= 15.4
Step-by-step explanation:
tanx = opp/adj
tan52° = x/12
x= tan52° * 12
x= 15.359
round -> 15.4
solve by substituting, show work
2x-3y=4
2x+8=11
Answers
Answer:
x=1.5 y=-1/3
Step-by-step explanation:
2x-3y=4
2x+8=11
Let's subtract 8 from both sides of the second equation:
2x=3
x=1.5
Substituting this into the first equation, we get:
2(1.5)-3y=4
3-3y=4
-3y=1
y=-1/3
Is this relation linear? Justify your answer.
Answers
Answer:
There is no image. Please repost.
What is the equation of the line that is perpendicular to y = 4x + 6 and passes through the point (8, −4)?
y equals negative one-fourth times x minus 2
y equals negative one-fourth times x plus 7
y = 4x − 36
y = 4x + 24
Answers
Answer:
1st: find the slope of the line that is perpendicular to y = 4x + 6 (which is m = -1/4)
2nd: substitute m = -1/4 x = 8 into y = mx + b and y = -4
3rd: Calculate it -4 = -1/4 x 8 + b
b = - 2
4th: substitute m = - 1/4 and b = -2 into y = mx + b
The final answer would be: y = -x/4 -2
Step-by-ste1p explanation:
what is the length and width of a basketball court
Answers
The length of a standard basketball court is 94 feet (28.65 meters), and the width is 50 feet (15.24 meters).
A standard basketball court is rectangular in shape and follows certain dimensions specified by the International Basketball Federation (FIBA) and the National Basketball Association (NBA). The length and width of a basketball court may vary slightly depending on the governing body and the level of play, but the most commonly used dimensions are as follows:
The length of a basketball court is typically 94 feet (28.65 meters) in professional settings. This length is measured from baseline to baseline, parallel to the sidelines.
The width of a basketball court is usually 50 feet (15.24 meters). This width is measured from sideline to sideline, perpendicular to the baselines.
These dimensions provide a standardized playing area for basketball games, ensuring consistency across different courts and facilitating fair play. It's important to note that while these measurements represent the standard dimensions, there can be slight variations in court size depending on factors such as the venue, league, or specific regulations in different countries.
Learn more about rectangular here:
https://brainly.com/question/21416050
#SPJ11
Two boats A and B Left a Port at the same time on different routes . B travelled on a bearing of 150º and A travelled on the North side of B . When A had travelled 8km and B had travelled 10km, the distance between the two boats was found to be 12km . Calculate the bearing of A's route from C.
Answers
Answer: 67.2°
Step-by-step explanation:
To find angle C, we have to use cosine rule. Therefore,
12² = 8² + 10² - 2 × 8 × 10 × cosC
C = 82.8°
The bearing of A from C will be
= 150° - 82.8°
= 67.2°.
How many different ways are there to choose a dozen donuts from the 4 varities at a donut shop so that you get atleast one donut of every variety g
Answers
There are 330 different ways for choosing a dozen donuts from the 4 varieties at a donut shop. (at least one donut of every variety must be selected)
How to calculate the number of ways to select items?There are 'r' items from 'n' different varieties (repetition allowed). Then, the number of ways to select items is given by
The number of ways = \(_{n+r-1}C_r\)
Where the combination \(_{n}C_r\) is calculated as
\(_{n}C_r=\frac{n!}{r!(n-r)!}\)
Calculation:It is given that there are 4 varieties of donuts in a shop. I.e., n = 4
Number of donuts to be selected r = 12 (one dozen)
And also given that at least one donut of every variety has to be selected.
Since there are 4 varieties, at least one from each of these means the count is 4.
So, the remaining number of donuts to be selected is 12 - 4 = 8.
So, r becomes 8 i.e., r = 8
On substituting,
the number of ways of selecting the remaining 8 donuts = \(_{4+8-1}C_4\)
⇒ \(_{11}C_4\)
⇒ \(\frac{11!}{4!(11-4)!}\)
⇒ \(\frac{11!}{(4!)(7!)}\)
⇒ 330
Therefore, there are 330 different ways for choosing a dozen donuts from the 4 varieties at a donut shop.
Learn more about combinations here:
https://brainly.com/question/11732255
#SPJ4
50 points and BRAINLIEST

Answers
Answer:
AZ = 12.80
Step-by-step explanation:
There are 2 triangles in the square XARS. Squares are always congruent, all sides are the same. Given that WT is 6, we can assume that RS is also 6 (because of congruency). RA is is the hypotenuse of the triangle ARS. To find AS, we can plug in the pythagorean theorem 6^2+x=^2=10^2. We end up getting square root of 64 which simplifies to 8. AS is now 8. We also know that ST is 6 since the square WRST has all congruent sides. 8+6=14 gives us line AT. TZ is 8 due to triangle XAR and the congruency theorem. Now we plug in pythagorean theorem to find AZ and we get 8^2+10^2=x^2. After simplifying the square root of 164, we see that AZ is equal to 12.80
Answer:
12.80
Step-by-step explanation:
SO IT IS 12.80 BECAUSE IT IS 12.80. SIMLIFY TO 12.8 SO YEAH!!
HOPE YOU UNDERSTAND.
Give exact answers for each of the following angles, in radians. Part A: \( \tan ^{-1}(-1) \) Answer: Part B: \( \tan ^{-1}(-\sqrt{3}) \) Answer:
Answers
For Part A,\(\( \tan ^{-1}(-1) \)\), the exact answer is\(\(-\frac{\pi}{4}\)\) radians. For Part B,\(\( \tan ^{-1}(-\sqrt{3}) \)\), the exact answer is \(\(-\frac{5\pi}{6}\)\) radians.
For Part A, the angle is \(\( \tan ^{-1}(-1) \)\). To find the exact answer in radians, we need to determine the angle whose tangent is equal to -1. The tangent function represents the ratio of the opposite side to the adjacent side in a right triangle. In this case, we are looking for an angle whose tangent is -1.
By examining the unit circle, we can see that the angle\(\( \frac{\pi}{4} \)\) (45 degrees) satisfies this condition. The tangent of \(\( \frac{\pi}{4} \)\)is indeed -1. Since we are working with radians, the answer for Part A is\(-\( \frac{\pi}{4} \)\).
For Part B, the angle is\(\( \tan ^{-1}(-\sqrt{3}) \)\). Again, we want to find the angle whose tangent is equal to \(-\(\sqrt{3}\)\). By analyzing the unit circle, we can determine that the angle \(\( \frac{5\pi}{6} \)\) (150 degrees) satisfies this condition. The tangent of\(\( \frac{5\pi}{6} \)\) is indeed \(-\(\sqrt{3}\)\). Hence, the answer for Part B is\(-\( \frac{5\pi}{6} \)\).
Learn more about radians
brainly.com/question/28990400
#SPJ11
What are the coordinates of the point on the directed line segment from (6,2) to (8,−10) that partitions the segment into a ratio of 1 to 3?
Answers
The coordinates of the point that divides the line segment from (6, 2) to (8, -10) into a ratio of 1 to 3 are (7, -1).
To find the coordinates of the point on the directed line segment that partitions it into a ratio of 1 to 3, we can use the concept of section formula.
The section formula states that if we have two points A(x₁, y₁) and B(x₂, y₂) dividing a line segment in the ratio of m₁ : m₂, then the coordinates of the dividing point P are given by:
Px = (m₁ * x₂ + m₂ * x₁) / (m₁ + m₂)
Py = (m₁ * y₂ + m₂ * y₁) / (m₁ + m₂)
In this case, the ratio is 1:3, which means m₁ = 1 and m₂ = 3. The given points are A(6, 2) and B(8, -10). Substituting these values into the formula, we can calculate the coordinates of the dividing point P:
Px = (1 * 8 + 3 * 6) / (1 + 3) = 7
Py = (1 * -10 + 3 * 2) / (1 + 3) = -2/2 = -1
Therefore, the coordinates of the point that divides the line segment from (6, 2) to (8, -10) into a ratio of 1 to 3 are (7, -1).
To find the coordinates of the point that divides the line segment between (6, 2) and (8, -10) in a 1:3 ratio, we can use the section formula. Applying the formula, where m₁ is 1 and m₂ is 3, the point P(x, y) can be determined.
By substituting the values into the formula, the x-coordinate is calculated as (1 * 8 + 3 * 6) / (1 + 3) = 7, and the y-coordinate is (1 * -10 + 3 * 2) / (1 + 3) = -1. Thus, the coordinates of the point that partitions the line segment into a ratio of 1 to 3 are (7, -1).
For more such questions segment,click on
https://brainly.com/question/28322552
#SPJ8
Find the circumference of the circle pictured above Round your answer to the nearest. hundredth 6
Answers
To find the circumference we have to calculate
\(s=2\pi r\)where r=6
therefore we have that the answer is
\(2\pi\cdot6=12\pi=37.699\approx37.70\)the price of a jar of peanut butter went from $ 5.99 to $ 6.89 . what was the percent change in the price?
Answers
Using Percentage formula , The change in the price of a jar of peanut butter is 15.02%.
Percentage : It is defined as a relative value indicating hundredth parts of any quantity. One percent (symbolized 1%) is a hundredth part.
First of we need to calculate difference between initial price and final price to
get the change in price.
Initial Price of jar of peanut butter = $ 5.99
Final price of jar of peanut butter = $ 6.89
Change in price of a jar of peanut butter = final price of jar of peanuts butter - initial price of jar of peanuts butter
= $ 6.89 - $ 5.99 = $ 0.9.
Percent change in price = ((Change in Price)/(initial price))× 100
percent change = (0.9/5.99)× 100 = 15.02
Hence, 15.02% is the change in price of a jar of peanuts butter.
To, learn more about percentage visit :
https://brainly.com/question/16797504
#SPJ4
"A box contains 8 crayons: 3 red, 2 blue, 1 black, 1 green, and 1 yellow. Remove one crayon from the box at random and set it apart, then remove a second crayon from the box. Use the conditional probability equation to find P (the second crayon is blue and the first crayon is blue)
Answers
The probability that the second crayon drawn is blue and the first crayon drawn is blue is 1/28.
To solve this problem, we can use the conditional probability formula:
P(A and B) = P(B|A) * P(A)
where:
P(A and B) is the probability that both events A and B occur
P(B|A) is the probability of event B given that event A has already occurred
P(A) is the probability of event A occurring
In this case, we want to find the probability of selecting a blue crayon on the second draw given that the first crayon selected was blue. So we have:
P(the second crayon is blue and the first crayon is blue) = P(blue on the second draw | blue on the first draw) * P(blue on the first draw)
To find each of these probabilities, we can start by calculating the total number of possible outcomes:
Total number of outcomes = 8 crayons in the box
Next, we need to find the probability of selecting a blue crayon on the first draw:
P(blue on the first draw) = 2/8 = 1/4
After the first blue crayon has been set aside, there are only 7 crayons left in the box, so the probability of selecting a blue crayon on the second draw given that the first crayon was blue is:
P(blue on the second draw | blue on the first draw) = 1/7
Putting it all together:
P(the second crayon is blue and the first crayon is blue) = P(blue on the second draw | blue on the first draw) * P(blue on the first draw)
= (1/7) * (1/4)
= 1/28
Therefore, the probability that the second crayon drawn is blue and the first crayon drawn is blue is 1/28.
To learn more about probability:
https://brainly.com/question/30034780
#SPJ4
2. The following set of count readings was made in a gradient-free γ-ray field, using a suitable detector for repetitive time periods of one minute: 18,500;18,410; 18,250;18,760;18,600;18,220;18,540;18,270;18,670;18,540. (a) What is the mean value of the number of counts? (b) What is its standard deviation (S.D.)? (c) What is the theoretical minimum S.D. of the mean? (d) What is the actual S.D. of a single reading? (e) What is the theoretical minimum S.D. of a single reading?
Answers
The inflection point of f(t) is approximately t = 3.73.
(a) To determine if the function f(t) = -0.425t^3 + 4.758t^2 + 6.741t + 43.7 is increasing or decreasing, we need to find its derivative and examine its sign.
Taking the derivative of f(t), we have:
f'(t) = -1.275t^2 + 9.516t + 6.741
To determine the sign of f'(t), we need to find the critical points. Setting f'(t) = 0 and solving for t, we have:
-1.275t^2 + 9.516t + 6.741 = 0
Using the quadratic formula, we find two possible values for t:
t ≈ 0.94 and t ≈ 6.02
Next, we can test the intervals between these critical points to determine the sign of f'(t) and thus the increasing or decreasing behavior of f(t).
For t < 0.94, choose t = 0:
f'(0) = 6.741 > 0
For 0.94 < t < 6.02, choose t = 1:
f'(1) ≈ 14.982 > 0
For t > 6.02, choose t = 7:
f'(7) ≈ -5.325 < 0
From this analysis, we see that f(t) is increasing on the intervals (0, 0.94) and (6.02, ∞), and decreasing on the interval (0.94, 6.02).
(b) To find the inflection point of f(t), we need to find the points where the concavity changes. This occurs when the second derivative, f''(t), changes sign.
Taking the second derivative of f(t), we have:
f''(t) = -2.55t + 9.516
Setting f''(t) = 0 and solving for t, we find:
-2.55t + 9.516 = 0
t ≈ 3.73
Therefore, The inflection point of f(t) is approximately t = 3.73.
Learn more about inflection point here:
https://brainly.com/question/29249123
#SPJ11
To determine the probability of threats, one has to
Select one:
a. multiply the risk by probability.
b. multiply the severity factor by probability factor
c. multiply the severity factor by risk factor
d. multiply the risk factor by likelihood factor
Answers
To determine the probability of threats, one has to:
d. multiply the risk factor by the likelihood factor.
The probability of a threat is typically calculated by considering the risk factor and the likelihood factor associated with the threat. Risk factor refers to the potential impact or severity of the threat, while the likelihood factor refers to the chance or probability of the threat occurring.
By multiplying the risk factor by the likelihood factor, one can assess the overall probability of a threat. This approach takes into account both the potential impact of the threat and the likelihood of it happening, providing a comprehensive understanding of the threat's probability.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
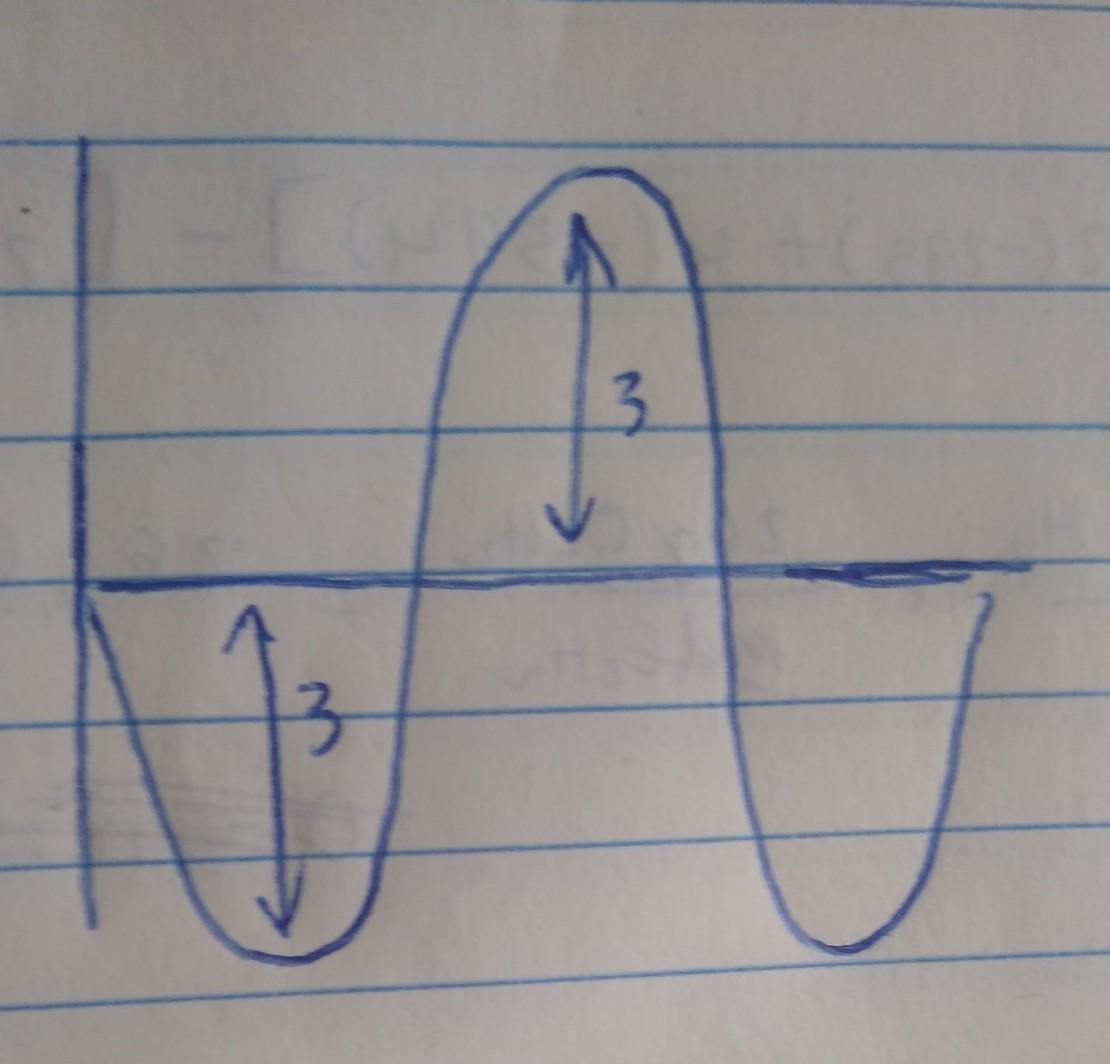
Choose the graph of y = -3 sin x.
Answers
Step-by-step explanation:
the graph should look something like this
Each ticket to the game costs $3.25. Someone buys 20 tickets. How much money did they spend on the tickets?
Answers
Answer:
$65
Step-by-step explanation:
20x3.25=65
The “Star Player” paradox haunts many pro athletes. For example, an NBA player may be highly rated, but their statistics don’t quite match up. For example, Lebron James in 2015 made 293 shots “outside the paint” (i.e., not under the basket). But his basket-scoring percentage this year when shooting at these distances was a dismal 34%. Roughly, how many of these baskets did he make?
Answers
Answer:
yay
Step-by-step explanation:
yayayayayayayayayayayayayayayayayayayayayayayayayayay
Show work will give 30 points NEED ASAP
2(5-10x)+8x=19x+52
Answers
Answer:
\(x=-\frac{42}{31}\)
Step-by-step explanation:
2 ( 5 - 10x ) + 8x = 19x + 52
→ Expand brackets
10 - 20x + 8x = 19x + 52
→ Simplify
10 - 12x = 19x + 52
→ Minus 19x from both sides
10 - 31x = 52
→ Minus 10 from both sides
-31x = 42
→ Divide both sides by -31
\(x=-\frac{42}{31}\)