a measure of relative fit for a simple regression line is called the r² or _ of _.

Answer:

Step-by-step explanation:

3x + 4x + x = 16

7x + x = 16

8x = 16

x = 16 : 8

x = 2

----------------------

3 × 2 + 4 × 2 + 2 = 16  (remember PEMDAS)

6 + 8 + 2 = 16

16 = 16

same value the answer is good

Answer:

3√5 is the answers for the question

Step-by-step explanation:

please mark me as brainlest

Answer:

B.

Step-by-step explanation:

the square root of 45 is about 6.708

the square root of 3 is about 1.732

the square root of 5 is about 2.236

the square root of 9 is 3

5 x 1.732 = 8.66

3 x 2.236 = 6.708

9 x 2.236 = 20.124

5 x 3 = 15

Answer: 2.5

Step-by-step explanation:

3 1.4 lbs also equals 3.25

3 x 0.75 = 2.25

2.25 + 25 = 2.5

The value of x and y in the algebra (3x - y, 2) = (2, x + y) ​ are 1 and 1 respectively.

An equation is an expression that shows how numbers and variables are related to each other using mathematical operators.

Given the algebra:

(3x - y, 2) = (2, x + y) ​

Therefore, equation:

3x - y = 2        (1)

Also:

x + y = 2        (2)

From both equations, solving simultaneously:

x = 1, y = 1

The value of x and y are 1 and 1 respectively.

Find out more on equation at: https://brainly.com/question/29174899

#SPJ1

We can fill in the boxes to make each equation complete as follows:

1. x³x⁹ = x¹²

2. x⁷/x³ = x⁴

3. 1/x⁻⁵ = x⁵

4. (7b³c⁵)³ = 343b⁹c¹⁵

To solve the exponents as provided above, the rules have to be factored in. One of the rules is that when multiplying exponents of the same base, we simply add their powers together. So, we have the powers of 3 and 9 for the first expression and they add up to 12.

1. x³x⁹ = x³ ⁺ ⁹ = x¹²

For the second expression, the rule of exponents says that when dividing, we will subtract the powers. This gives us x⁴ for the second expression.

2. x⁷/x³ = x⁷ ⁻ ³ = x⁴

Learn more about exponents here:

https://brainly.com/question/13669161

#SPJ1

Answer:

Smaller than

Positive numbers

Step-by-step explanation:

The absolute value of a number is the distance from the zero. This can be positive or negative forming the absolute number. The distance is negative when the number is positive. The absolute numbers are used in the equations for the solutions. The numbers greater than zero are positive numbers.

Let's assume that x represents the number of square feet in the garden, and y represents the number of carrots that can be grown at a time.

We are given that when the garden is 2 square feet, she can grow 8 carrots at a time. This suggests a linear relationship between x and y.

To find the equation, we can use the concept of proportionality. Since the number of carrots grown is directly proportional to the area of the garden, we can set up a proportion:

x/y = 2/8

Cross-multiplying, we have:

8x = 2y

Dividing both sides by 2, we get:

4x = y

So, the equation for the relationship between x and y is y = 4x.

learn more about:- square feet here

https://brainly.com/question/30678567

#SPJ11

Answer:

Proportional

Step-by-step explanation:

A proportional graph is a straight line that passes through the origin.

A non-proportional graph can be a straight line, but it does NOT pass through the origin.

Therefore, this is a proportional graph.

Hope this helps :)

Answer:

it is 300 i think

300.

The midpoint is 300 because the distance from the 2 points is 100 so 300.

Answer:

int option 3

Step-by-step explanation:

Answer:

I think it is option 4

Step-by-step explanation:

could be 3 possiblyu

Answer: 7:8

Step-by-step explanation: just subtract 150-80 and you get 70

80 is the women

The remaining 70 is the men

Now arrange it to men:women

70:80

Now simplify

7:8

Hope that helps :)

Answer:

  34 square units

Step-by-step explanation:

You want the area of the triangle with vertices X(6, 8), Y(3, 3), and Z(13, -3).

There are several ways the area of a triangle can be calculated from the coordinates of the vertices. One relatively easy method is to find half the absolute value of the sum of the determinants of adjacent pairs of points.

This calculation is shown in the second attachment.

The area of ∆XYZ is 34 square units.

A slope calculation will tell you side XY is perpendicular to side YZ. This means you can find the area from the lengths of these two sides. The distance formula can tell you the lengths.

  XY = √((3 -6)² +(3 -8)²) = √(9 +25) = √34

  YZ = √((13 -3)² +(-3 -3)²) = √(100 +36) = 2√34

 Area = 1/2bh = (1/2)(√34)(2√34) = 34 . . . . square units

Pick's theorem tells you the area of a polygon with vertices on grid points can be found by counting the grid points on the boundary and interior to the boundary.

  A = i + (b/2) -1

This triangle has the three given vertices on grid points, along with point (8, 0), which is the midpoint of YZ. There are 33 interior points, so the area is ...

  A  = 33 +(4/2) -1 = 34 . . . . square units

The length of XZ is ...

  XZ = √((13 -6)² +(-3 -8)²) = √(49 +121) = √170

Heron's formula tells you the area is given by ...

  A = √(s(s -a)(s -b)(s -c)) . . . . . . where s = (a+b+c)/2, the semiperimeter

The third attachment shows this calculation gives an area of 34 square units.

__

Additional comments

The slope calculation tells you the slope of XY is ...

  m = (y2 -y1)/(x2 -x1) = -5/-3 = 5/3

and the slope of YZ is ...

  m = -6/10 = -3/5 . . . . . . . . the opposite reciprocal of the slope of XY

Hence these sides are perpendicular, as we noted above.

We like Pick's theorem for finding the areas of small figures with irrational side lengths (such as this one). It just involves counting, which is often easier than using a bunch of different formulas for slope or length.

The determinant formula is easy to compute, but tedious to enter on a calculator. It is much easier to program a spreadsheet for this. As with Pick's theorem, the method applies to a polygon with any number of vertices.

  \(\left|\begin{array}{cc}a&b\\c&d\end{array}\right|=ad-bc\)

In these 2×2 matrices, the coordinates can be listed in rows or in columns. It makes no difference to the calculation. The key is to work in one direction around the figure. (Here, we went CCW.)

The triangle is drawn in the first attachment. The geometry program that drew it also calculated its area to be 34 square units.

You may have noticed that the "determinant" method and Pick's theorem guarantee that the area of any polygon with integer coordinates will be an integer multiple of 1/2 square unit. That is, it will never be irrational. (You might not see that using Heron's formula.)

#95141404393

Answer:

3/2y-5

Step-by-step explanation:

The expression – 1/2 (–3y + 10) is equivalent to the expression (3/2)y – 5.

The equivalent is the expressions that are in different forms but are equal to the same value.

The expression is given below.

⇒ – 1/2 (–3y + 10)

Simplify the equation, we have

⇒ (3/2)y – 5

More about the equivalent link is given below.

https://brainly.com/question/889935

#SPJ2

The response y(t) graphically, we can first plot the individual functions h(t) and x(t) on a graph, and then determine their convolution to obtain y(t). Let's go step by step:

Plotting h(t):

The function h(t) is defined as h(t) = [u(t-1) - u(t-4)].

The unit step function u(t-a) is 0 for t < a and 1 for t ≥ a. Based on this, we can plot h(t) as follows:

For t < 1, h(t) = [0 - 0] = 0

For 1 ≤ t < 4, h(t) = [1 - 0] = 1

For t ≥ 4, h(t) = [1 - 1] = 0

So, h(t) is 0 for t < 1 and t ≥ 4, and it jumps up to 1 between t = 1 and t = 4. Plotting h(t) on a graph will show a step function with a jump from 0 to 1 at t = 1.

Plotting x(t):

The function x(t) is defined as x(t) = t[u(t) - u(t-2)].

For t < 0, both u(t) and u(t-2) are 0, so x(t) = t(0 - 0) = 0.

For 0 ≤ t < 2, u(t) = 1 and u(t-2) = 0, so x(t) = t(1 - 0) = t.

For t ≥ 2, both u(t) and u(t-2) are 1, so x(t) = t(1 - 1) = 0.

So, x(t) is 0 for t < 0 and t ≥ 2, and it increases linearly from 0 to t for 0 ≤ t < 2. Plotting x(t) on a graph will show a line segment starting from the origin and increasing linearly with a slope of 1 until t = 2, after which it remains at 0.

Obtaining y(t):

To obtain y(t), we need to convolve h(t) and x(t). Convolution is an operation that involves integrating the product of two functions over their overlapping ranges.

In this case, the convolution integral can be simplified because h(t) is only non-zero between t = 1 and t = 4, and x(t) is only non-zero between t = 0 and t = 2.

The convolution y(t) = h(t) * x(t) can be written as:

y(t) = ∫[1,4] h(τ) x(t - τ) dτ

For t < 1 or t > 4, y(t) will be 0 because there is no overlap between h(t) and x(t).

For 1 ≤ t < 2, the convolution integral simplifies to:

y(t) = ∫[1,t+1] 1(0) dτ = 0

For 2 ≤ t < 4, the convolution integral simplifies to:

y(t) = ∫[t-2,2] 1(t - τ) dτ = ∫[t-2,2] (t - τ) dτ

Evaluating this integral, we get:

\(y(t) = 2t - t^2 - (t - 2)^2 / 2,\) for 2 ≤ t < 4

For t ≥ 4, y(t) will be 0 again.

Maximum value of y(t):

To find the value of t at which y(t) reaches its maximum value, we need to examine the expression for y(t) within the valid range 2 ≤ t < 4. We can graphically determine the maximum by plotting y(t) within this range and identifying the peak.

Plotting y(t) within the range 2 ≤ t < 4 will give you a curve that reaches a maximum at a certain value of t. By visually inspecting the graph, you can determine the specific value of t at which y(t) reaches its maximum.

Learn more about function here:

https://brainly.com/question/11624077

#SPJ11

Standard deviation of the following data is 0.655.

The standard deviation is equal to the variance's positive square root. It is a fundamental statistical analysis method. The amount by which data values deviate from the mean is referred to as "standard deviation," or "SD."

Whereas a big standard deviation implies that the values are much outside the mean, a low standard deviation shows that the values are frequently only a few standard deviations from the mean.

Here in the question,

Total kids = 20.

Mean = 9+9.5+9.5+10+10+10+10+10.5+10.5+10.5+10.5+11+11+11+11+11+11+11.5+11.5+11.5/20

= 10.52

Now square of distance between mean and ages.

(9-10.52) ² = 2.31

(9.5-10.52) ² = 1.04

(10-10.52) ² = 0.27

(10.5-10.52) ² = 0.0004

(11-10.52) ² = 0.23

(11.5-10.52) ² = 0.96

Now sum of all the differences = 2.31 + 1.04 + 1.04 + 4×0.27 + 4× 0.0004 + 6× 0.23+ 3×0.96

= 8.73

Now standard deviation = √8.73/20

= √0.43

= 0.655

To know more about standard deviation, visit:

https://brainly.com/question/23907081

#SPJ1

Answer:

Percentages express the scale of something when the maximum number is known. In these problems, the maximum number is always followed by "out of" for example 12 out of 43 means that the macimum number is 43 and we are at 12 (our present value) so how close are we to 43?

Simply divide the present value by the maximum number and multiply by 100 to get the percentages

12/43 x 100

Answer:

the answer to your first question is 235 degrees or B

the answer to your second question is 83 degrees

Step-by-step explanation:

for the first question simply add all of the angles

for the second question a straight line/angle is 180 degrees so simply subtract 97 from 180 to get 83 degrees

The sampling distribution of the sample mean will always have the same the mean of the original non-normal distribution, as the original distribution.

What is distribution?

Each of these samples contains a mean, and if we add up all of the means, we can construct a probability distribution that explains the distribution of the means. As long as we have sufficient samples, as will be discussed later, this distribution is always normal and is referred to as the sampling distribution of the sample mean.

Since the sample mean's sampling distribution is normal, we can naturally calculate the distribution's mean and standard deviation and utilise that information to analyse probability questions.

Here, The sample variance is equal to the population variance divided by the sample size if the population is infinite and the sampling is random, or if the population is finite but we are sampling with replacement.

So we need to use the mean of non-normal distribution.

Hence the answer will be the mean of the original non-normal distribution.

Learn more about distribution, by the following link.

https://brainly.com/question/13781953

#SPJ4

Answer:

these teachers b expectin u to do this bs

Step-by-step explanation:

a) To create a comparative boxplot for ZOD (Zone Out Duration) by pie type, we would separate the ZOD data into two groups: apple pie and cherry pie.

The boxplots will provide a visual comparison of the distributions for the two groups. By examining the boxplots, we can determine if there appears to be a difference between the ZODs for the two groups. b) Using the set.seed(12) command to ensure reproducibility, we can create 1000 permutations of the difference in mean ZOD for cherry pie minus the mean ZOD for apple pie. The observed difference in means for the sample data would be the actual difference between the mean ZODs of the cherry pie and apple pie groups.

c) The statistical hypotheses for testing that the mean ZOD for cherry pie is greater than the mean ZOD for apple pie can be expressed as: Null hypothesis (H0): The mean ZOD for cherry pie is less than or equal to the mean ZOD for apple pie. (μcherry ≤ μapple). Alternative hypothesis (HA): The mean ZOD for cherry pie is greater than the mean ZOD for apple pie. (μcherry > μapple). d) To visualize the null distribution, we would make a histogram using the 1000 permutations. The number of bins would be set to 13. The null distribution represents the distribution of the differences in means under the assumption that there is no difference between cherry pie and apple pie ZODs. We would add a vertical line to indicate the observed sample difference in means.

e) By conducting the permutation test and setting up the code correctly, we can calculate the p-value. If the code is correct, the p-value obtained should be 0.002. This p-value represents the probability of observing a difference in means as extreme as the one observed in the sample data, assuming that there is no actual difference between cherry pie and apple pie ZODs. f) Based on the hypothesis test and the obtained p-value of 0.002, we can conclude that there is strong evidence to reject the null hypothesis. The results suggest that the mean ZOD for cherry pie is significantly greater than the mean ZOD for apple pie. In the context of the problem, it indicates that consuming cherry pie at lunch, two hours before class, leads to a higher Zone Out Duration during the lecture compared to consuming apple pie.

To learn more about probability, click here: brainly.com/question/16988487

#SPJ11

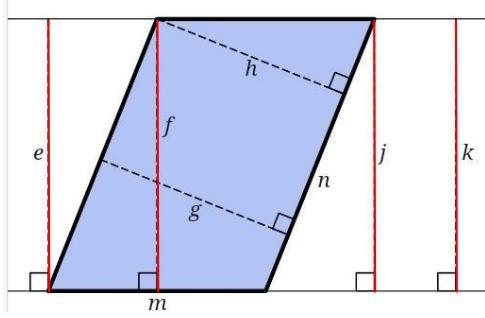
height or altitude for a parallelogram means the perpendicular distance from one parallel side to the other.  Check the picture below.

Answer:

16

Step-by-step explanation:

let boys equal to 5x

and girls equal to 4x

so 4x+5x=36

X=4

so boys are 5*4

boys are 20

and girls are 16

so boys are 4 more than girls

Answer:

16 girls

Step-by-step explanation:

boys : girls : total

5          4        5+4 = 9

take the total number of people and divide by 9

36/9 = 4

Each number should be multiplied by 4

boys : girls : total

5*4        4*4     9*4

20          16        36

There are 16 girls

Answer:

L=18, W=8

Step-by-step explanation:

Given :

Area (A)=144 \(m^2\) =LW

Where, L is length and W is width

According to given question ,

\(W=\frac{1}{3} L-2\)

Now,

A=LW

144=L\((\frac{1}{3} L-2)\)

432=\(L^{2} -6L\)

\(L^{2} -6L-432=0\\L^{2} -18L+24L-432\\(L+24) (L-18)\\L=-24\\and L=18\)

Length can be in negative so L =18

And

\(LW=144\\18W=144\\W=\frac{144}{18} \\W=8\)

Therefore, Length of rectangle is 18 and Width is 8

Rounding to the nearest whole value, we get the estimated number of observations above 118 as 2940.

To determine the number of observations expected to be below a certain value using the 68-95-99.7 Rule, we need to find the area under the normal distribution curve up to that value.

For the first scenario:

Mean (μ) = 162

Standard deviation (σ) = 11

Value to evaluate (x) = 195

We want to find the area under the curve to the left of x = 195. This corresponds to the cumulative probability of a value being less than 195 in a normal distribution.

Using a standard normal distribution table or a calculator, we can find that the cumulative probability for x = 195 is approximately 0.961. This means that about 96.1% of the observations are expected to be below 195.

To find the number of observations, we multiply the cumulative probability by the total number of observations:

Number of observations = 0.961 * 2400 = 2306.4

Rounding to the nearest single observation, we get the estimated number of observations below 195 as 2306.

For the second scenario:

Mean (μ) = 137

Standard deviation (σ) = 19

Value to evaluate (x) = 118

We want to find the area under the curve to the right of x = 118. This corresponds to the cumulative probability of a value being greater than 118 in a normal distribution.

Using the same approach, we can find that the cumulative probability for x = 118 is approximately 0.735. This means that about 73.5% of the observations are expected to be above 118.

To find the number of observations, we multiply the cumulative probability by the total number of observations:

Number of observations = 0.735 * 4000 = 2940

learn more about whole value here

https://brainly.com/question/12086644

#SPJ11

The ratio of change in the area of a rectangle, given that the length has increased in the ratio 3:2 and the width has reduced in the ratio 4:5 and the ratio of change in the area of the rectangle is 1.2, indicating a 20% increase in the area from the original size.

Let's calculate the new length and width of the rectangle. The original length is 18 cm, and it has increased in the ratio 3:2. So, the new length can be calculated as (18 cm) * (3/2) = 27 cm. Similarly, the original width is 15 cm, and it has reduced in the ratio 4:5. Hence, the new width can be calculated as (15 cm) * (4/5) = 12 cm.

The original area of the rectangle is (18 cm) * (15 cm) = 270 cm². The new area is (27 cm) * (12 cm) = 324 cm². Therefore, the ratio of change in the area can be calculated as (324 cm²) / (270 cm²) = 1.2.

Hence, the ratio of change in the area of the rectangle is 1.2, indicating a 20% increase in the area from the original size.

Learn more about ratio here:

https://brainly.com/question/13419413

#SPJ11

Answer:

A

Step-by-step explanation

0 -4 -1 1 2

theyre also all in bold correct order as should be

Answer:

A

Step-by-step explanation:

-4 is left from point 0

-1 is one step left from 0

1 and 2 is right from 0

Answer:

B

Step-by-step explanation:

The sum of the inner angles of a quadrilateral is 360 degrees

135 + 110 + 68 + x = 360

313 + x = 360

x = 47 degrees

Answer:

47

Step-by-step explanation:

whole thing is 360 degrees

68 + 110 + 135 = 313

360 - 313 = 47

x looks small too (if you had to guess in a multiple choice question)

The mean of all exam scores in the class is found as 71.

For the given question;

The z-score is found by;

z = (x - μ)/σ

x =  sample mean

μ =  mean score

σ =  standard deviation

Now, from this,

x = zσ + μ

For p = 80th percentile= 0.8, see z value from z score table.

z = 0.85

x = 85 points

85 = 0.85σ +  μ  .....eq 1

For p = 30% = 0.3, see z value from z score table.

z = -0.3802

x = 65

65 = -0.3802σ +  μ  .....eq 2

Solving eq 1 and 2.

σ = 16.25

Put in eq 1

μ = 71.19

μ = 71

Thus, the mean of all exam scores in the class is found as 71.

To know more about the normally distributed, here

https://brainly.com/question/23418254

#SPJ4