A set of ordered pairs is called what?
Answers
Answer:
A relation
Step-by-step explanation:
Answer:
A relation is a set of ordered pairs. The set of all first components of the ordered pairs is called the domain of the relation and the set of all second components of the ordered pairs is called the range of the relation.
Step-by-step explanation:
Related Questions
From the parent function, how has the equation y = (x+3)² been shifted?
Up 3
Down 3
Right 3
Left 3
Answers
The translation in y = (x + 3)² is of 3 units to the left. The correct option is the last one.
How has the equation been shifted?For a general function y = f(x), we define a horizontal translation of N units as:
g(x) = f(x + N)
if N > 0, the shift is to the left.if N < 0, the shift is to the right.Here the original function is y = x² and the translated one is:
y = (x + 3)²
So we just added 3 on the argument, so this is a shift of 3 units to the left, the correct option is the last one.
Learn more about translations at:
https://brainly.com/question/24850937
#SPJ1
8x+y=5 and x+y=12 , using substitution and elimination
Answers
Answer:
x=−1,y=13
Step-by-step explanation:
Answer:
x = -1 and y = 13 Please Mark Brainliest
Step-by-step explanation:
Nork Facior out the GCF from the polynomial a^(5)b^(7)-a^(3)b^(2)+a^(2)b^(6)-a^(2)b^(2)
Answers
The GCF of the polynomial a^(5)b^(7)-a^(3)b^(2)+a^(2)b^(6)-a^(2)b^(2) is a^(2)b^(2), and the factored form of the polynomial is a^(2)b^(2)(a^(3)b^(5)-a+b^(4)-1).
The GCF, or greatest common factor, is the largest factor that all terms in a polynomial have in common. In this case, we need to find the GCF of the polynomial a^(5)b^(7)-a^(3)b^(2)+a^(2)b^(6)-a^(2)b^(2).
First, we need to look at the exponents of each term to determine the GCF. The smallest exponent for a is 2, and the smallest exponent for b is 2. Therefore, the GCF for this polynomial is a^(2)b^(2).
Next, we need to factor out the GCF from each term in the polynomial. This is done by dividing each term by the GCF and then multiplying the GCF by the resulting polynomial.
So, the factored form of the polynomial is:
a^(2)b^(2)(a^(3)b^(5)-a+b^(4)-1)
To know more about GCF click on below link:
https://brainly.com/question/11444998#
#SPJ11
A survey of statistics undergraduate at prosperity university completed a survey that asked for their verbal and math sat scores. They wanted to predict the verbal score based on the math score. The value of r-squared was 12. 78%. The least squares regression equation is yhat = 383. 3 + 0. 3489x. Find r.
Answers
The coefficient of determination (r-squared) provides an indication of how well the regression model fits the data and the value of r is 0.3574
In this example, the r-squared value is 12.78%, which means that 12.78% of the variation in verbal SAT scores can be explained by the variation in math SAT scores. The least squares regression equation is yhat = 383.3 + 0.3489x, where yhat is the predicted verbal score and x is the math score.
The coefficient of correlation (r) provides a measure of the strength of the linear relationship between two variables. In this example, the coefficient of correlation (r) can be calculated from the coefficient of determination (r-squared) as follows: r = √r-squared = √12.78% = 0.3574. This indicates that there is a weak linear relationship between verbal and math SAT scores.
For more questions like R-squared click the link below:
https://brainly.com/question/13324767
#SPJ4
what is the last digit of 3 with a power of 2011
Answers
So to find any last digit of 3^2011 divide 2011 by 4 which comes to have 3 as remainder. Hence the number in units place is same as digit in units place of number 3^3. Hence answer is 7.
The Food Marketing Institute shows that 17% of households spend more than $100 per week on groceries. Assume the population proportion is and a simple random sample of households will be selected from the population. Use the z-table.
Answers
A) The sample proportion = 0.17, and standard error/deviation = 0.013281
B) 0.869
C)0.9668
A) We know that 17% of households spend more than $100 per week on groceries. We are given that p ( the proportion of the population that spends more than $100 per week) = 0.17
sample size (n)= 800
The sample proportion of p = 0.17
The standard error of p will be calculated using this formula =
\(\sqrt{\frac{p(1-p)}{n} }\) =\(\sqrt{\frac{0.17(1 - 0.17)}{800} }\)
= 0.013281
B) We have to find the probability that the sample proportion will be +-0.02 of the population proportion
= p (0.17 - 0.02 ≤ P ≤ 0.17 + 0.02 ) = p( 0.15 ≤ P ≤ 0.19)
z value corresponding to P
Z = (P - p)/std deviation at P = 0.15
Z = (0.15 - 0.17) / 0.013281 = -1.51
at P = 0.19
z = ( 0.19 - 0.17) / 0.013281 = 1.51
Therefore the required probability will be
p( -1.5 ≤ z ≤ 1.5 ) = p(z ≤ 1.51 ) - p(z ≤ -1.51 )
= 0.9345 - 0.0655 = 0.869
C) Now, we have to find the same probability for a sample (n ) = 1600
standard deviation/ error = 0.009391 (applying the equation for calculating standard error as seen in part A above)
Therefore the required probability after applying;
z = (P - p)/std deviation at p = 0.15 and p = 0.19
p ( -2.13 ≤ z ≤ 2.13 ) = p( z ≤ 2.13 ) - p( z ≤ -2.13 )
= 0.9834 - 0.0166 = 0.9668
Therefore,
A) The sample proportion = 0.17, and standard error/deviation = 0.013281
B) 0.869
C)0.9668
To learn more about sample proportion;
https://brainly.com/question/33127920
#SPJ4
The complete question is " The Food Marketing Institute shows that 17% of households spend more than $100 per week on groceries. Assume the population proportion is p = .17 and a sample of 800 households will be selected from the population. a. Show the sampling distribution of p, the sample proportion of households spending more than $100 per week on groceries. b. What is the probability that the sample proportion will be within ±.02 of the population proportion? c. Answer part (b) for a sample of 1600 households."
solve and show working
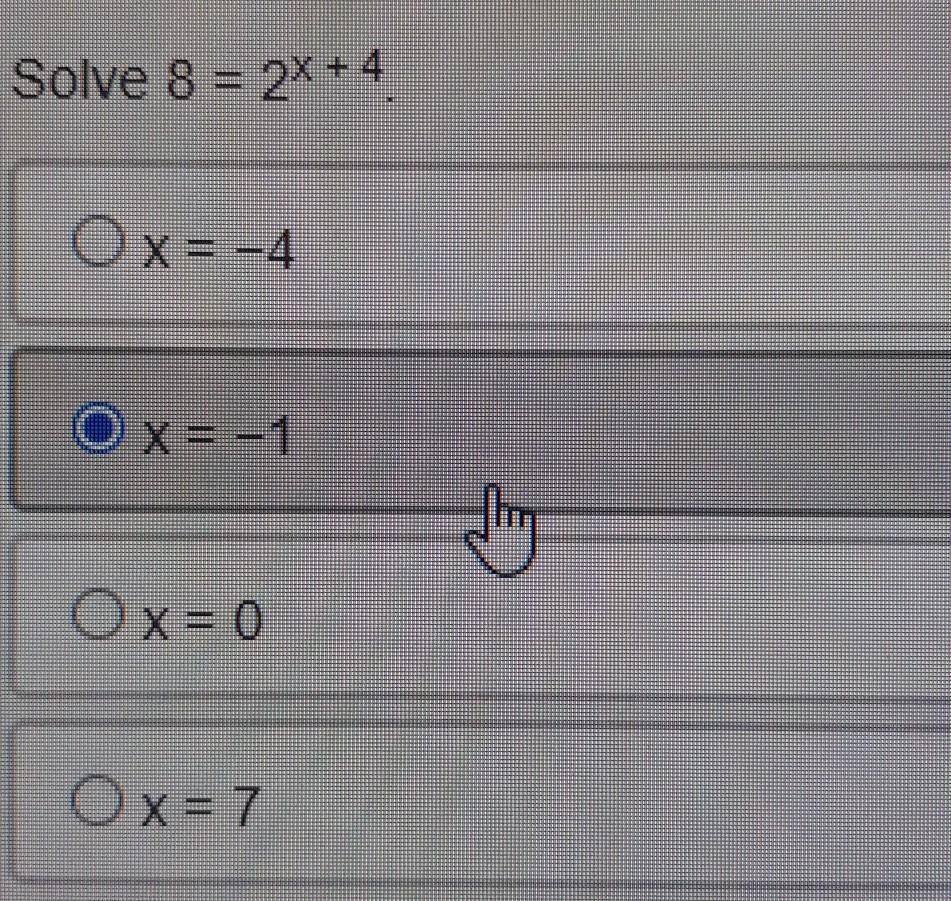
Answers
Answer:
\(\huge\boxed{\sf x = -1}\)
Step-by-step explanation:
Given equation:\(8=2^{x+4}\)
Factorize 8\(2 \times 2 \times 2=2^{x+4}\\\\2^3=2^{x+4}\)
Comparing both sides, we get:3 = x + 4
Subtract 4 from both sides3 - 4 = x
-1 = x
OR
x = -1\(\rule[225]{225}{2}\)
State all integer values of x in the interval [-5,0] that satisfy the following inequality 4x+7>-9
Answers
• Integer values: ,numbers including 0, and negative and positive numbers; it can never be a fraction, a decimal, or a percent.
Based on the definition, the integer values included in the interval [-5, 0] are: -5, -4, -3, -2, -1, and 0.
To evaluate if the integer satisfies the inequality, we have to evaluate each integer.
• -5
\(4\cdot(-5)+7>-9\)\(-20+7>-9\)\(-13>-9\)As -13 is smaller than -9, then -5 does not satisfy the inequality.
• -4
\(4\cdot(-4)+7>-9\)\(-16+7>-9\)\(-9>-9\)As -9 is equal to -9, then -4 does not satisfy the inequality (as in the sign of the inequality it is not included -9).
• -3
\(4\cdot(-3)+7>-9\)\(-12+7>-9\)\(-5>-9\)As -5 is bigger than -9, -3 satisfies the inequality.
• -2
\(4\cdot(-2)+7>-9\)\(-8+7>-9\)\(-1>-9\)As -1 is bigger than -9, -2 satisfies the inequality.
• -1
\(4\cdot(-1)+7>-9\)\(-4+7>-9\)\(3>-9\)As 3 is bigger than -9, -1 satisfies the inequality.
• 0
\(4\cdot(0)+7>-9\)\(7>-9\)As 7 is bigger than -9, 0 satisfies the inequality.
Also we can try by solving the inequality:
\(4x+7>-9\)\(4x>-9-7\)\(x>\frac{-16}{4}\)\(x>-4\)Meaning that all the values that are greater than -4 but not -4.
Answer:
• [-3, 0]
,• x = -3, -2, -1, 0
,• x > -4
find an algebraic expression for the particle's velocity vx at a later time t . express your answer in terms of the variables c , t , v0x , and m .
Answers
The algebraic expression for the particle's velocity vₓ at a later time t is v(t) = ct²/2m +v₀ₓ.
Given that,
c = speed of light
t = time
v₀ₓ = initial velocity of particle
m = mass of particle
Velocity and acceleration are related through time. Acceleration is the rate of change of velocity, which is represented graphically as the slope of the velocity vs. time line. Velocity can be represented as the area underneath an acceleration vs. time line.
Newton's second law declares that an object having mass m will accelerate due to a net force (F) will accelerate at a rate of:
α = F/m
Therefore, the function that describes the acceleration at any point in time of the particle is:
α(t)=ct/m
The velocity function is the integral of the acceleration function, so we get:
v(t)= ∫ct/m dt
= ct²/2m +C
where the constant C is the initial velocity of the particle at time t=0. Therefore, the velocity function representing the velocity at any point in time is:
v(t) = ct²/2m +v₀ₓ
Therefore, the algebraic expression for the particle's velocity vₓ at a later time t is v(t) = ct²/2m +v₀ₓ.
Learn more about the velocity here:
https://brainly.com/question/30559316.
#SPJ12
what is the sequence of 8,2,0,2,8,18
Answers
Answer:
Step-by-step explanation:
32
Answer:
32
Step-by-step explanation:
using a formula for the variance of a sample, what is the denominator?
Answers
The denominator of the formula for the variance of a sample is given as follows:
N - 1.
What is a fraction?A fraction is a numerical representation of the division of the two terms x and y that composed the fraction, as follows:
Fraction = x/y.
The terms are named as follows:
The top term x is the numerator of the fraction.The bottom term y is the denominator of the fraction.The formula for the variance of a sample is given as follows:
\(s^2 = \frac{sum (X - \overbar{X})^2}{N - 1}\)
Hence the denominator is the bottom term, which is of N - 1.
More can be learned about fractions at https://brainly.com/question/21610929
#SPJ1
Choose the correct simplification of the expression (xyz2)4. (1 point) x5y5z6 x5y5z8 xyz16 x4y4z8
Answers
The simplification of the expression (xyz²)⁴ will be; (x)⁴y⁴z⁸
Since Expression is defined as the collection of numbers variables and functions by using signs like addition, subtraction, multiplication, and division.
WE are Given the exponential expression
(xyz²)⁴
Expand the expression as;
(x)⁴y⁴(z²)⁴
According to the indices rule:
(xyz²)⁴ = (x)⁴y⁴z⁸
Hence the correct simplification of the expression as;
(xyz²)⁴ = (x)⁴y⁴z⁸
Learn more on indices here:
brainly.com/question/10339517
#SPJ4
A pair of sunglasses is priced at $42.95. They are put on sale at 27% off the original price. Shane estimates the discounted price of the sunglasses to be around $36. Is this a reasonable estimate?
A. No, the estimate should be lower.
B. No, the estimate should be higher.
C. Yes, the estimate is reasonable.
Answers
Answer: C. Yes, the estimate is reasonable.
Step-by-step explanation:
The answer in my opinion should be A.
Please please help!!

Answers
Answer:
The explicit formula is \(a_{n}\) = - 13 - 7n
Step-by-step explanation:
Let us at first find the type of the sequence
∵ The terms are - 20, - 27, - 34, - 41, ............
→ Find the difference between each to consecutive terms
∵ - 27 - (- 20) = - 27 + 20 = - 7
∵ - 34 - (- 27) = - 34 + 27 = - 7
∵ - 41 - (- 34) = - 41 + 34 = - 7
→ There is a constant difference between each two consecutive terms
∴ The sequence is Arithmetic
→ The explicit formula of the nth term of the arithmetic sequence is
\(a_{n}=a+(n-1)d\), wherea is the first termd is the constant differencen is the position of the number∵ a = - 20
∵ d = -7
∴ \(a_{n}=-20+(n-1)(-7)\)
→ Simplify it
∴ \(a_{n}\) = - 20 + (-7)(n) - (-7)(1)
∴ \(a_{n}\) = - 20 + (-7n) - (-7)
∴ \(a_{n}\) = - 20 - 7n + 7
→ Add the like terms
∴ \(a_{n}\) = (- 20 + 7) - 7n
∴ \(a_{n}\) = - 13 - 7n
The explicit formula is \(a_{n}\) = - 13 - 7n
The green triangle is a dilation of the red triangle with a scale factor of s=13 and the center of dilation is at the point (4,2)
What are the coordinates of Point C'? C'(___,____)
What are the coordinates of Point A? A(____,____)

Answers
Given:
Scale factor \(s=\dfrac{1}{3}\)
Center of dilation = (4,2)
To find:
The coordinates of the points C' and A.
Solution:
We know that, if a figure is dilated with a scale factor k and the center of dilation is at the point (a,b), then
\((x,y)\to (k(x-a)+a,k(y-b)+b)\)
The scale factor is \(\dfrac{1}{3}\) and the center of dilation is at (4,2).
\((x,y)\to (\dfrac{1}{3}(x-4)+4,\dfrac{1}{3}(y-2)+2)\) ...(i)
Suppose the vertices of red triangle are A(m,n), B(10,14) and C(-2,11).
Using rule (i), we get
\(C(-2,11)\to C'(\dfrac{1}{3}(-2-4)+4,\dfrac{1}{3}(11-2)+2)\)
\(C(-2,11)\to C'(\dfrac{1}{3}(-6)+4,\dfrac{1}{3}(9)+2)\)
\(C(-2,11)\to C'(-2+4,3+2)\)
\(C(-2,11)\to C'(2,5)\)
Hence, the coordinates of Point C' are C'(2,5).
Let us assume that point A is A(m,n).
Using rule (i), we get
\(A(m,n)\to A'(\dfrac{1}{3}(m-4)+4,\dfrac{1}{3}(n-2)+2)\)
From the given figure it is clear that the image of point A is (8,4).
\(A'(\dfrac{1}{3}(m-4)+4,\dfrac{1}{3}(n-2)+2)=A'(8,4)\)
On comparing both sides, we get
\(\dfrac{1}{3}(m-4)+4=8\)
\(\dfrac{1}{3}(m-4)=8-4\)
\((m-4)=3(4)\)
\(m=12+4\)
\(m=16\)
And,
\(\dfrac{1}{3}(n-2)+2=4\)
\(\dfrac{1}{3}(n-2)=4-2\)
\((n-2)=3(2)\)
\(n=6+2\)
\(n=8\)
Therefore, the coordinates of point A are (16,8).
7
When you raise a number to the
second power or a power of 2, you
could say that you
the
number
Answers
Answer:
is multiplied by itself.
Step-by-step explanation:
2 to the second power is four, and so is 2 times 2.
7 to the second power is 49, and so is 7 times 7.
They are the same thing.
Hope this helps!
For example 7 to the 2nd power would be the equation
7 x 7 = 49
and 7 to the 3rd power would be
7 x 7 x 7 = 343
What is 4 ( x − 1 ) ≥ 2 x + 6 as an improper fraction?
Answers
Answer:
18/5
Step-by-step explanation:
you have to times then divide
In regression analysis, if the dependent variable is measured in dollars, the independent variable _____.
Answers
In regression analysis, if the dependent variable is measured in dollars, the independent variable can be units.
What are dependent and independent variables in regression analysis?The outcome variable is also called the response or dependent variable, and the risk factors and confounders are called the predictors, or explanatory or independent variables. In regression analysis, the dependent variable is denoted "Y" and the independent variables are denoted by "X".The variable that is used to explain or predict the response variable is called the explanatory variable. It is also sometimes called the independent variable because it is independent of the other variable.To learn more about Dependent and Independent Variable, refer to:
https://brainly.com/question/3764906
#SPJ4
It takes Nadia 12 days to build a cubby house. If she and Vincent work together, they can finish building a cubby house in 8 days. Find the number of days, h, that it will take Vincent to build a cubby house by himself.
Answers
It will take Vincent 24 number of days to build the cubby house by himself.
Let's assume that Vincent can build the cubby house alone in h days.
From the given information, we know that Nadia takes 12 days to build the cubby house, and when Nadia and Vincent work together, they can finish it in 8 days.
We can use the concept of "work done" to solve this problem. The amount of work done is inversely proportional to the number of days taken.
Nadia's work rate is 1/12 of the cubby house per day, while the combined work rate of Nadia and Vincent is 1/8 of the cubby house per day.
When Nadia and Vincent work together, their combined work rate is the sum of their individual work rates:
1/8 = 1/12 + 1/h
To solve for h, we can rearrange the equation:
1/h = 1/8 - 1/12
1/h = (3 - 2) / 24
1/h = 1/24
Taking the reciprocal of both sides, we find:
h = 24
for more such questions on equation
https://brainly.com/question/17145398
#SPJ8
in the land of maggiesville, a random sample of 2500 people were surveyed. if it is true that 8% of people in maggiesville are knitters, what is the probability that the sample proportion will be between 5% and 10%?
Answers
The probability that the sample proportion of knitters in a random sample of 2500 people from Maggiesville will be between 5% and 10% is approximately 0.9644, or 96.44%.
what is the probability that the sample proportion will be between 5% and 10%?To find the probability that the sample proportion of knitters will be between 5% and 10%, we can use the normal approximation to the binomial distribution.
The sample proportion can be modeled as a binomial distribution with parameters n (sample size) and p (true proportion). In this case, n = 2500 and p = 0.08.
To apply the normal approximation, we need to calculate the mean (μ) and the standard deviation (σ) of the sample proportion. The mean of a binomial distribution is μ = n * p, and the standard deviation is σ = √(n * p * (1-p)).
μ = 2500 * 0.08 = 200
σ = √(2500 * 0.08 * 0.92) ≈ 10.954
Next, we need to standardize the values of 5% and 10% using the z-score formula:
z1 = (0.05 - 0.08) / 0.010954 ≈ -2.741
z2 = (0.10 - 0.08) / 0.010954 ≈ 1.827
Now, we can use the standard normal distribution table or a calculator to find the probabilities associated with these z-scores.
P(5% ≤ sample proportion ≤ 10%) = P(-2.741 ≤ z ≤ 1.827)
By looking up the z-scores in the standard normal distribution table or using a calculator, we find:
P(-2.741 ≤ z ≤ 1.827) ≈ 0.9644
Therefore, the probability that the sample proportion of knitters will be between 5% and 10% is approximately 0.9644, or 96.44%.
Learn more on probability here;
https://brainly.com/question/251701
#SPJ4
how do you slove -3 (6x-1)=-24
Answers
Answer:
x = 3/2
Step-by-step explanation:
Step 1: Write equation
-3(6x - 1) = -24
Step 2: Solve for x
Distribute: -18x + 3 = -24
Subtract 3 on both sides: -18x = -27
Divide both sides by -18: x = 3/2
Step 3: Check
Plug in x to verify if it's a solution.
-3[6(1.5) - 1) = -24
-3[9 - 1] = -24
-3[8] = -24
-24 = -24
I need help on this assignment
Answers
Since TV bisects ∠STU:
\(\begin{gathered} m\angle STV=m\angle UTV \\ besides\colon \\ m\angle STU=m\angle STV+m\angle UTV \\ so\colon \\ m\angle STU=2(m\angle UTV) \end{gathered}\)A spinner is divided into six equal parts numbered 1, 2, 3, 4, 5, and 6. In a repeated experiment, Ryan spun the spinner twice. The theoretical probability of both spins being odd numbers is 9 over 36.
If the experiment is repeated 140 times, predict the number of times both spins will be odd numbers.
140
70
36
35
Answers
So, based on the theoretical likelihood, we anticipate that 35 times out of 140 repeats, both spins will be odd numbers.
What is probability?Probability is a branch of mathematics that deals with the study of random events and the likelihood of their occurrence. Probability is expressed as a number between 0 and 1, with 0 indicating that an event is impossible to occur and 1 indicating that an event is certain to occur. The probability of an event A, denoted by P(A), is calculated as the number of favorable outcomes for the event divided by the total number of possible outcomes. For example, if a fair six-sided die is rolled, the probability of rolling a 3 is 1/6 because there is only one favorable outcome (rolling a 3) out of the total 6 possible outcomes. Probabilities can be used to make predictions about the likelihood of future events and to make decisions under uncertainty. Probabilities can also be used to describe the distribution of random variables and to quantify the relationship between different events. Probability theory is widely used in many fields, such as statistics, engineering, finance, physics, and biology, among others.
Here,
The theoretical probability of both spins being odd numbers is 9 over 36, which means that for every 36 times the experiment is repeated, we expect 9 of those times to result in both spins being odd numbers.
If the experiment is repeated 140 times, we can use the theoretical probability to estimate the number of times both spins will be odd numbers as follows:
140 * (9/36) = 35
So, based on the theoretical probability, we predict that both spins will be odd numbers 35 times out of 140 repetitions.
To know more about probability,
https://brainly.com/question/30034780
#SPJ1
Find the solution of
x^2y′′ + 5xy′ + (4+6x)y = 0, x>0 of the
form
[infinity]
y1=x^r ∑ cn x^n
n=0
where c0=1. Enter
r=
cn=
Answers
The solution of the given differential equation is y = x⁴ ∑ (-1)ⁿ [(n+3)(n+4)(n+5)...(2n+3)]/[(n!)(3)(2)(1)] and the value of r is 4 and the value of cₙ is (-1)ⁿ [(n+3)(n+4)(n+5)...(2n+3)]/[(n!)(3)(2)(1)].
Given: x²y′′ + 5xy′ + (4+6x)y = 0, x > 0.
To find: The solution of the given differential equation in the form y₁ = x^r ∑ cₙ xⁿ n=0, where c₀=1.
Solution: Let's assume the solution of the given differential equation is of the form y₁=x^r ∑ cₙ xⁿ n=0---(1).
Differentiating (1) w.r.t x, we get y′=rx^(r-1) ∑ cₙ xⁿ + x^r ∑ ncₙ x^(n-1)---(2).
Differentiating (2) w.r.t x, we get
y′′=r(r-1)x^(r-2) ∑ cₙ xⁿ + 2rx^(r-1) ∑ ncₙ x^(n-1) + x^r ∑ n(n-1)cₙ x^(n-2)---(3).
Now substitute (1), (2) and (3) in the given differential equation, we get,
x²[r(r-1)x^(r-2) ∑ cₙ xⁿ + 2rx^(r-1) ∑ ncₙ x^(n-1) + x^r ∑ n(n-1)cₙ x^(n-2)] + 5x[rx^(r-1) ∑ cₙ xⁿ + x^r ∑ ncₙ x^(n-1)] + (4+6x)x^r ∑ cₙ xⁿ = 0
On simplification, we get,
∑ [(r(r-1)cₙ + 5rcₙ + (4+6(n+1))cₙ) x^(r+n)] = 0
Hence, we get the following recurrence relation:
r(r-1)cₙ + 5rcₙ + (4+6(n+1))cₙ = 0
⇒ r(r+4)cₙ = -(6n+4)cₙ
⇒ cₙ₊₁/cₙ = - (r+n+3)(r+n+2)/(r+4)
On solving the recurrence relation, we get
cₙ = (-1)ⁿ [r(r+1)(r+2)(r+3)...(r+n-1)]/[(n!)(4)(3)(2)(1)]
Since c₀=1
⇒ c₀ = (-1)⁰ [r(r+1)(r+2)(r+3)...(r+0-1)]/[(0!)(4)(3)(2)(1)]
⇒ 1 = r/4
⇒ r = 4
Hence, the solution of the given differential equation is
y = y₁
= x⁴ ∑ cₙ x^ⁿ
= x⁴ ∑ (-1)ⁿ [(4)(5)(6)...(4+n-1)]/[(n!)(4)(3)(2)(1)]
y = x⁴ ∑ (-1)ⁿ [(n+3)(n+4)(n+5)...(2n+3)]/[(n!)(3)(2)(1)]
Therefore, the value of r is 4 and the value of cₙ is (-1)ⁿ [(n+3)(n+4)(n+5)...(2n+3)]/[(n!)(3)(2)(1)].
To know more about differential equation, visit:
https://brainly.com/question/25731911
#SPJ11
in a manufacturing process, a random sample of 36 manufactured bolts has a mean length of 3 inches with a standard deviation of .3 inches. what is the 99 percent confidence interval for the true mean length of the manufactured bolt?
Answers
The 99% confidence interval for the true mean length of the manufactured bolt is (2.9177, 3.0823)
Here, we need to construct a 99% confidence interval for population mean (μ) is given by
μ = x + Zα/2 * σ/√n or μ = x - Zα/2 * σ/√n
where, μ = population mean
x = sample mean
= 3 inches
σ = population standard deviation
= 0.3 inches
Zα/2= z score for a two tailed test at level of significance α = 2.576( for a 99% confidence level)
So, the upper limit would be,
μ = 3 + 1.645 * (0.3/√36)
μ = 3 + 1.646 * (0.3/6)
μ = 3.0823
And the lower limit would be,
μ = 3 - 1.645 * (0.3/√36)
μ = 3 - 1.646 * (0.3/6)
μ = 2.9177
Hence, the 99% confidence interval is (2.9177, 3.0823)
Learn more about confidence interval here:
https://brainly.com/question/24131141
#SPJ4
A construction crew is lengthening a road that originally measured 51 miles. The crew is adding one mile to the road each day. The length, L (in miles), after d days of construction is given by the following.
L= 51+d
What is the length of the road after 38 days?
Answers
Answer: 89 miles
Step-by-step explanation:
Well, if the construction crew added one mile every day for 38 days, then the formula would look like this.
L = 51 + (38)
51 + 38 = 89
L = 89 miles
WILL GIVE BRAINLIST
Find the indicated term of each sequence by repeatedly multiplying the first term by the common ratio. Enter your answer to 5 decimal places if necessary. Use a calculator.
−30, 6, −1.2, ...; 5th term
The 5th term of the sequence is
Answers
Answer:
-0.048
Step-by-step explanation:
-30 * -1/5 = 6
6 * -1/5 = -1.2
(Remember -30 is first term so we subtract 1 from 5 in the exponent)
-30 * (-1/5)^4 = -0.048
Find the percent error of the measurement.
0.2 cm
A.
25%
B.
50%
C.
400%
Answers
Answer:
0.2
Step-by-step explanation:
In a class of 34 students,19 of them are girls.
What percentage of the class are girls?
Give your answer to 1 decimal place
Answers
Answer:
55.9%
Step-by-step explanation:
To find the percentage of girls in the class, we can use the following formula:
Percentage = (Number of girls / Total number of students) * 100
Number of girls = 19
Total number of students = 34
Percentage = (19 / 34) * 100
= 55.88235 % ≈ 55.9 % ( rounded off to one decimal place)
Madison and Tyler each wrote an expression that is equivalent to 14.1 (19.8 + 7.6). The expressions they created are shown in the table.
Expressions Madison and Tyler Created
Student
Expression
Madison
14.1 (7.6 + 19.8)
Tyler
14.1 (19.8) + 14.1 (7.6)
Answers
Answer: Tyler used the distributive property.
Step-by-step explanation:
For the expression:
Madison wrote: which is by commutative property of addition.
The commutative property of addition says that , for a,b be any real number
Tyler wrote: which is by distributive propery.
The distributive property says that , for a,b,c be any real numbers.
Hence, the last option is correct.
Answer:
D
Step-by-step explanation:
Took the test ;)