A square has an area of 1 square unit. What is the length of the square?
Answers

Related Questions
Between which two integers does - 1 3/4 lie?
A) -2 and -1
B) -1 and 0
C) 0 and 1
D) 1 and 2

Answers
A machine is shut down for repairs if a random sample of 100 items selected from the daily output of the machine reveals at least 15% defectives. (Assume that the daily output is a large number of items.) Suppose that a random sample of 20 items is selected from the machine. If the machine produces 20% defectives, find the probability that the sample will contain at least three defectives, by using the following methods. (a) the normal approximation to the binomial (Round your answer to four decimal places.)
Answers
Answer:
0.7995 = 79.95% probability that the sample will contain at least three defectives.
Step-by-step explanation:
Binomial probability distribution
Probability of exactly x sucesses on n repeated trials, with p probability.
Can be approximated to a normal distribution, using the expected value and the standard deviation.
The expected value of the binomial distribution is:
\(E(X) = np\)
The standard deviation of the binomial distribution is:
\(\sqrt{V(X)} = \sqrt{np(1-p)}\)
Normal probability distribution
Problems of normally distributed distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
When we are approximating a binomial distribution to a normal one, we have that \(\mu = E(X)\), \(\sigma = \sqrt{V(X)}\).
Suppose that a random sample of 20 items is selected from the machine.
This means that \(n = 20\)
The machine produces 20% defectives
This means that \(p = 0.2\)
Mean and standard deviation:
\(\mu = E(X) = np = 20*0.2 = 4\)
\(\sigma = \sqrt{V(X)} = \sqrt{np(1-p)} = \sqrt{20*0.2*0.8} = 1.79\)
Probability that the sample will contain at least three defectives
Using continuity correction, this is \(P(X \geq 3 - 0.5) = P(X \geq 2.5)\), which is 1 subtracted by the pvalue of Z when X = 2.5. So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{2.5 - 4}{1.79}\)
\(Z = -0.84\)
\(Z = -0.84\) has a pvalue of 0.2005
1 - 0.2005 = 0.7995
0.7995 = 79.95% probability that the sample will contain at least three defectives.
In trapezoid ABCD, line AC is a diagonal and angle ABC is congruent to angle ACD. Find AC if the lengths of the bases line BC and line AD are 12m and 27m, respectively
Answers
Since ΔABC and ΔACD are similar triangles, therefore the length of AC is 18 m.
What are Similar Triangles?Similar triangles are triangles with corresponding sides that have the same ratio.
Thus:
AD is parallel to BC (bases of a trapezoid are parallel)
Therefore:
∠ACB = ∠CAD (alternate interior angles)
This implies that, ΔABC ~ ΔACD by AA similarity theorem.
Thus:
AC/DA = CB/AC
Substitute
AC² = 12 × 27
AC = √324
AC = 18 m
Therefore, since ΔABC and ΔACD are similar triangles, therefore the length of AC is 18 m.
Learn more about similar triangles on:
brainly.com/question/11899908
#SPJ1
this please help me
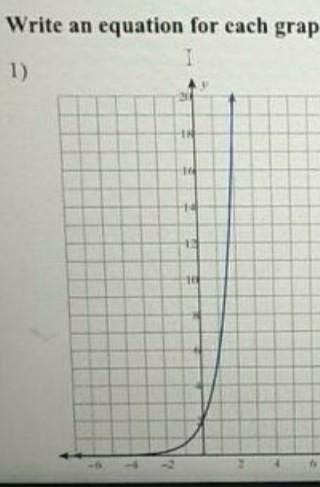
Answers
9514 1404 393
Answer:
y = 2·3^x
Step-by-step explanation:
The shape of the graph appears exponential. The horizontal asymptote appears to be y=0, so there is no vertical offset. The y-intercept seems to be 2 (we can't really read the numbers), and the y-value seems to increase by a factor of 3 for each additional unit of x.
The multiplier is 2, and the base of the exponential factor is 3. That gives us ...
y = 2(3^x)
Find the slope of the line passing through the points (-3, -2) and (9,-2).
slope:
Answers
Answer:
Step-by-step explanation:
(-2+2)/(9+3)= 0/12= 0
y + 2 = 0(x + 3)
y + 2 = 0
y = -2
cheetan brought a 2L bottle of milk and used 400 ml from it with the remaining amount of milk he could complely fill 8 glases of the same size and shape
Please Give Answer Fast
Answers
The number of millimeters in each glass is 200ml.
How to illustrate the expression?It is important to note that an expression is simply used to show the relationship between the variables that are provided or the data given regarding an information. in this case, it is vital to note that they have at least two terms which have to be related by through an operator.
It is important to note that some of the mathematical operations that are illustrated in this case include addition, subtraction, etc.
Since Cheetan brought a 2L bottle of milk and used 400 ml from it with the remaining amount of milk he could complely fill 8 glases of the same size and shape. The amount in each will be:
= (2l - 400ml )/8
= (2000 - 400) / 8
= 1600 / 8
= 200ml
Therefore, based on the calculation, there'll be 200 millimeters on each glass.
Learn more about expressions on:
brainly.com/question/723406
#SPJ1
Complete question
cheetan brought a 2L bottle of milk and used 400 ml from it with the remaining amount of milk he could complely fill 8 glases of the same size and shape. How many ml will each contain?
How many ways can a committee of 2 be selected from a club with 12 members?
Select one:
a. 132
О O
b. 33
О O
c. 2
d. 66
O
Answers
have a good day :)
the C means combination cuz the order doesn’t matter
please answer 10 points and brainliest
drag the tiles to correct boxes to complete the pairs.
what x-value makes the set of ratios equivelent?
6
9
16
25
---------
match these with the numbers.
2:3=6:x
4:7=x:42
2x:48=3:12
12:15=x:20
------
please answer quickly i need to get this done by tomorrow.
Answers
Answer:
9, 24, 6, 16
Step-by-step explanation:
6/2 = x/3
x = 3*3 = 9
42/7 = x/4
x = 6*4 = 24
48/12 = 2x/3
2x = 4*3 = 12
x = 6
20/15 = x/12
x = 4/3*12 = 16
1. A target is divided into 100 squares colored in dark blue, white, and light blue. Amber throws a beanbag that lands on the target.
co
9 25
dark blue
What is the probability that it will land on a dark blue square?
26
white
light blue

Answers
The probability of landing on the dark blue target is 2/5.
Finding probabilityProbability is the ratio of required to the total possible outcomes of an event.
The required outcome = dark blue= 25Total possible outcomes= entire sample Space = 100P(dark blue ) = 40/100
divide through by 20
P(dark blue ) = 2/5
Therefore, the probability of landing on target is 2/5
Learn more on probability:https://brainly.com/question/24756209
#SPJ1
5/100 in simplest form
Answers
Answer:1/20
Step-by-step explanation:
trust
Answer:
1/20
Step-by-step explanation:
5 divided by 100 is =20
5divided by 5 is =1
=1/20
aznswer answer
-3p ≥ 30 solve
Answers
\(-3p \geq 30\\\\\\\implies p \leq -\dfrac{30}3~~~~;[\text{Multiplying by a negative number so reverse the inequality}]\\\\\\\implies p \leq -10 \\\\\text{Interval,} ~~ (-\infty, -10]\)
Kristin bought a pack of 12
pencils for $1.25. How
much was each pencil?
Answers
Given the points P (3, 5) and Q (-5, 7) on the cartesian plane such that R (x, y) is
the midpoint of PQ, find the equation of the line that passes through R and
perpendicular
to PQ.
Answers
Answer:
-22=22
Step-by-step explanation:
3,5-5,7=
-22/22
The equation of the line passing through R and PQ is 4(y - 6) = -x - 1/2.
To find the equation of the line passing through the midpoint R and the points P and Q, we first need to find the coordinates of the midpoint R. The midpoint coordinates can be found by taking the average of the x-coordinates and the average of the y-coordinates of P and Q.
The x-coordinate of the midpoint R is (3 + (-5)) / 2 = -1/2.
The y-coordinate of the midpoint R is (5 + 7) / 2 = 6.
So, the coordinates of the midpoint R are (-1/2, 6).
Next, we can use the two-point form of the equation of a line, which states that the equation of the line passing through points (x₁, y₁) and (x₂, y₂) is given by:
(y - y₁) = (y₂ - y₁) / (x₂ - x₁) \(\times\) (x - x₁)
Substituting the coordinates of R (-1/2, 6) and P (3, 5) into the equation, we have:
(y - 6) = (7 - 5) / (-5 - 3) \(\times\)(x - (-1/2))
Simplifying the equation:
(y - 6) = (2 / -8) \(\times\)(x + 1/2)
(y - 6) = -1/4 \(\times\)(x + 1/2)
4(y - 6) = -x - 1/2
Therefore, the equation of the line passing through R and PQ is 4(y - 6) = -x - 1/2.
For more such answers on coordinates
https://brainly.com/question/30227780
#SPJ8
Round 782,317.772 to the nearest whole number.
Answers
Nearest whole number will be 782318.
Nearest ones whole number is the first digit before the decimal point of a number.
For example nearest ones of 9.6 is equal to 10.
If the tenth digit (first number before decimal point) of the number is greater than or equal to 5 we round up and add 1 to ones of number, If the tenth digit of the number is less than 5 we remove the decimal part. Example:
124.6
The first number of right of decimal point is 6
6 is greater than 5, so we add 1.
Result = 125
Now given number is 782317.772
since the first digit after decimal is 7 which is greater than 5 thus the nearest whole number will be 782318.
Learn more about nearest whole number here:
https://brainly.com/question/23064461
#SPJ4
Triangles DEF and D'E'F' are shown on the coordinate plane below: H F D D' 2 -8-7--5-4-3-2-1 1 2 3 4 5 6 7 8 T 20 F CO What rotation was applied to triangle DEF to create triangle D'E'F'?
Answers
No
100 Points! Geometry question. Photo attached. Please show as much work as possible. Thank you!

Answers
Answer:
\(BC=5.1\)
\(B=23^{\circ}\)
\(C=116^{\circ}\)
Step-by-step explanation:
The diagram shows triangle ABC, with two side measures and the included angle.
To find the measure of the third side, we can use the Law of Cosines.
\(\boxed{\begin{minipage}{6 cm}\underline{Law of Cosines} \\\\$c^2=a^2+b^2-2ab \cos C$\\\\where:\\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides.\\ \phantom{ww}$\bullet$ $C$ is the angle opposite side $c$. \\\end{minipage}}\)
In this case, A is the angle, and BC is the side opposite angle A, so:
\(BC^2=AB^2+AC^2-2(AB)(AC) \cos A\)
Substitute the given side lengths and angle in the formula, and solve for BC:
\(BC^2=7^2+3^2-2(7)(3) \cos 41^{\circ}\)
\(BC^2=49+9-2(7)(3) \cos 41^{\circ}\)
\(BC^2=49+9-42\cos 41^{\circ}\)
\(BC^2=58-42\cos 41^{\circ}\)
\(BC=\sqrt{58-42\cos 41^{\circ}}\)
\(BC=5.12856682...\)
\(BC=5.1\; \sf (nearest\;tenth)\)
Now we have the length of all three sides of the triangle and one of the interior angles, we can use the Law of Sines to find the measures of angles B and C.
\(\boxed{\begin{minipage}{7.6 cm}\underline{Law of Sines} \\\\$\dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c} $\\\\\\where:\\ \phantom{ww}$\bullet$ $A, B$ and $C$ are the angles. \\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides opposite the angles.\\\end{minipage}}\)
In this case, side BC is opposite angle A, side AC is opposite angle B, and side AB is opposite angle C. Therefore:
\(\dfrac{\sin A}{BC}=\dfrac{\sin B}{AC}=\dfrac{\sin C}{AB}\)
Substitute the values of the sides and angle A into the formula and solve for the remaining angles.
\(\dfrac{\sin 41^{\circ}}{5.12856682...}=\dfrac{\sin B}{3}=\dfrac{\sin C}{7}\)
Therefore:
\(\dfrac{\sin B}{3}=\dfrac{\sin 41^{\circ}}{5.12856682...}\)
\(\sin B=\dfrac{3\sin 41^{\circ}}{5.12856682...}\)
\(B=\sin^{-1}\left(\dfrac{3\sin 41^{\circ}}{5.12856682...}\right)\)
\(B=22.5672442...^{\circ}\)
\(B=23^{\circ}\)
From the diagram, we can see that angle C is obtuse (it measures more than 90° but less than 180°). Therefore, we need to use sin(180° - C):
\(\dfrac{\sin (180^{\circ}-C)}{7}=\dfrac{\sin 41^{\circ}}{5.12856682...}\)
\(\sin (180^{\circ}-C)=\dfrac{7\sin 41^{\circ}}{5.12856682...}\)
\(180^{\circ}-C=\sin^{-1}\left(\dfrac{7\sin 41^{\circ}}{5.12856682...}\right)\)
\(180^{\circ}-C=63.5672442...^{\circ}\)
\(C=180^{\circ}-63.5672442...^{\circ}\)
\(C=116.432755...^{\circ}\)
\(C=116^{\circ}\)
\(\hrulefill\)
Additional notes:
I have used the exact measure of side BC in my calculations for angles B and C. However, the results will be the same (when rounded to the nearest degree), if you use the rounded measure of BC in your angle calculations.
slope of line (-3,-2) and (-1,-5)
Answers
Answer:
−3/2
Step-by-step explanation:
Hope this helps
:D
Point A has coordinates (-6, -2), and point B has coordinates (-4,6). What is the slope of a line segment connecting the two?

Answers
Answer:
6-(-2)/(-4+6) 8/2=4
Step-by-step explanation:
Y2-y1/x2-x1
The slope of the given line is m = 4.
Given,
Point A has coordinates (-6, -2).
Point B has coordinates (-4,6).
We need to find what is the slope of a line segment connecting the two.
What is the slope of a line between two points?If the two points are (x_1, y_1) and (x_2, y_2).
Then the slope is given by:
m = (y_2 - y_1) / (x_2 - x_1)
Find the slope.
Let,
(-6, -2) = (x_1, y_1)
(-4, 6) = (x_2, y_2)
m = (y_2 - y_1) / (x_2 - x_1)
m = (6 - (-2)) / (-4 - (-6))
m = (6 + 2) / (-4 + 6)
m = 8 / 2
m = 4
Thus the slope of the given line is m = 4.
Learn more about the slope of a line between two points here:
https://brainly.com/question/18298097
#SPJ2
I WILL GIVE BRAINLIEST PLEASE

Answers
Answer:
4
Step-by-step explanation:
Answer:
The answer is 6/25
Step-by-step explanation:
Both 24 and 100 are divisible by 4 so:
24/4 = 6 and 100/4 = 25
So, your final answer is 6/25
help please!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
to find the interest you simply just multiply the amount by the percentage, so:
$3000 × 3.5%
= $3000÷100×3.5
=$105
show work if possible

Answers
Answer:
B. 14,525
Step-by-step explanation:
If a tablet costs $35 and the school is purchasing tablets for every student, then the total cost to buy tablets for the whole school would be:
$35 x 415 = $14,525
Therefore, the answer is B. $14,525.
The 95% confidence interval for these parts is 56.98 to 57.05 under normal operations. A systematic sample is taken from the manufacturing line to determine if the production process is still within acceptable levels. The mean of the sample is 56.96. What should be done about the production line
Answers
Answer:
Stop the line of production since the sample mean (56.96) is outside the confidence interval [\(CI_{0.95}\) = ( 56.98, 57.05 )]
Step-by-step explanation:
Given that;
95% confidence interval for these parts is 56.98 to 57.05
\(CI_{0.95}\) = ( 56.98, 57.05 )
Sample mean = 56.96
We know that;
If the sample mean is within the confidence interval then, our decision is to keep the line operating as it is inside the confidence interval.
But if the sample mean is not within the confidence interval them, our decision is to stop the line of production as it is outside the confidence interval.
Now since our mean sample (56.96) does not lie between with the 95% confidence interval \(CI_{0.95}\) = ( 56.98, 57.05 ).
Therefore, Stop the line of production since the sample mean (56.96) is outside the confidence interval [\(CI_{0.95}\) = ( 56.98, 57.05 )]
Among all pairs of numbers whose sum is 24, find a pair whose product is as large as possible. Show the work(the steps)! Write an equation of the corresponding quadratic function. How parabola opens? What is the maximum product? Does this function has a maximum value or the minimum value? Explain. Graph the function and upload the image.
Answers
The pair of numbers that yields the maximum product when their sum is 24 is (12, 12), and the maximum product is 144. The corresponding quadratic function is P(x) = -x^2 + 24x, and the parabola opens downwards.
To find a pair of numbers whose sum is 24 and whose product is as large as possible, we can use the concept of maximizing a quadratic function.
Let's denote the two numbers as x and y. We know that x + y = 24. We want to maximize the product xy.
To solve this problem, we can rewrite the equation x + y = 24 as y = 24 - x. Now we can express the product xy in terms of a single variable, x:
P(x) = x(24 - x)
This equation represents a quadratic function. To find the maximum value of the product, we need to determine the vertex of the parabola.
The quadratic function can be rewritten as P(x) = -x^2 + 24x. We recognize that the coefficient of x^2 is negative, which means the parabola opens downwards.
To find the vertex of the parabola, we can use the formula x = -b / (2a), where a = -1 and b = 24. Plugging in these values, we get x = -24 / (2 * -1) = 12.
Substituting the value of x into the equation y = 24 - x, we find y = 24 - 12 = 12.
So the pair of numbers that yields the maximum product is (12, 12). The maximum product is obtained by evaluating the quadratic function at the vertex: P(12) = 12(24 - 12) = 12(12) = 144.
Therefore, the maximum product is 144. This quadratic function has a maximum value because the parabola opens downwards.
To graph the function, you can plot several points and connect them to form a parabolic shape. Here is an uploaded image of the graph of the quadratic function: [Image: Parabola Graph]
For more such question on function. visit :
https://brainly.com/question/11624077
#SPJ8
What’s the mean of 46,57,66,63,49,52,61,68
Answers
Answer:
Step-byHow do I calculate the mean?
The mean can be calculated only for numeric variables, no matter if they are discrete or continuous. It's obtained by simply dividing the sum of all values in a data set by the number of value
-step explanation:
46+57+66+63+49+52+61+68= 462/8 the total number of observation
the answer 57
the answer 57
Kenji is playing the video game Dragon Tamer, where players go on adventures finding and training dragons. In the first level of the game, he gets 10 points for finding a Silverthorn Dragon but gets
–
6 points when it scorches him with fire.
Answers
I really need point
In a triangle ABC, which is the longest side if:
a) <A is a right angle
b) <C is a right angle
Answers
Answer:
a) BC is the longest side
b) AB is the longest side
✌️
Graph the line with the equation y = -1/5 x + 4.
Answers
the equation straight line y = -1/5 x + 4. of the line drawn in the picture is attached below.
What is equation straight line?
There are numerous ways to express the equation of a straight line, including point-slope form, slope-intercept form, general form, standard form, etc. A straight line is a geometric object with two dimensions and infinite lengths at both ends. The formulas for the equation of a straight line that are most frequently employed are y = mx + c and axe + by = c. Other versions include point-slope, slope-intercept, standard, general, and others.
Given two line-side coordinates, use the slope formula to determine the slope of the line. The slope is defined as the ratio of the change in the y values to the change in the x values using the formula m=(y2-y1)/(x2-x1).
The given equation y = -1/5 x + 4.
Here m = -1/5
and c= 4
So the plot on the graph will be as fallow.
Hence the equation of the line drawn in the picture attached below
Learn more about the straight line, by the following link
https://brainly.com/question/16949303
#SPJ1

write an equation, g(x), for the transformations of the parent function, f(x) =x , when it is reflected across the y-axis and translated down 5 units
Answers
Answer:
\(g(x)=-x-5\)
Step-by-step explanation:
if we reflect across the y-axis, the y-value is just being negated, or in other words from positive -> negative or negative -> positive depending on what the initial y-value was.
So if we have the function \(f(x)=x\), then we just negate the x, since the x represents the y-value.
This gives us: \(g(x)=-x\)
Now to translate 5 units down, the y-value is decreasing by 5 units, and since the -x represents the y-value, we just subtract 5 from it to get
\(g(x)=-x-5\)
3/8=4/7x what is x please help me omg
Answers
The value of the variable x = 21/32
What are algebraic expressions?Algebraic expressions are simply described as expressions that are composed of variables, coefficients, terms, constants and factors.
These expressions are also made up of certain arithmetic or mathematical operations.
These operations includes;
SubtractionDivisionAdditionMultiplicationBracketParenthesesFrom the information given, we have that;
3/8=4/7x
cross multiply the values, we have;
7x(3) = 8(4)
multiply the values and expand the brackets, we get the values;
21x = 32
Divide both sides by the coefficient of the variable x, we get;
x = 32/21
Learn about algebraic expressions at: https://brainly.com/question/4344214
#SPJ1
Find the solution of the system for which

Answers
Answer:
3,0,-6,0
Step-by-step explanation:
x1=3 because 3+0+0=3
since x2 and s2=0.