Arlene has to unpack 4 1/2 boxes of canned pineapple juice. He unpacked 1/4 of them.
How many boxes are still unpacked?
Answers
To find out how many boxes are still unpacked, we need to subtract the fraction Arlene has already unpacked from the total number of boxes.
Total boxes: 4 1/2
Fraction unpacked: 1/4
To subtract fractions, we need a common denominator. In this case, the common denominator is 4.
4 1/2 = 9/2 (as an improper fraction)
Now we can subtract:
9/2 - 1/4 = 18/4 - 1/4 = 17/4
So, Arlene still has 17/4 (or 4 1/4) boxes of canned pineapple juice left to unpack.
I hope this helps! ;)
Related Questions
please help me find the area

Answers
The calculated area of the composite figure is 129 square units
Calculating the area of the composite figureGiven that we have
A composite figure
To find the area of a composite figure, you can break it down into smaller, simpler shapes whose areas you can calculate. Then you can add up the areas of these shapes to get the total area of the composite figure.
The area is then calculated as
Area = Trapezoid + Rectangle + Parallelogram + Triangle
Using the dimensions from the graph, we have
Area = 1/2 * (12 + 6) * 4 + 6 * 10 + 3 * 7 + 1/2 * 6 * 4
Evaluate
Area = 129
Hence, the area is 129 square units
Read more about area at
https://brainly.com/question/22972014
#SPJ1
what is the great common factor of 6 and 8?
Answers
The answer to your question is 2
Choose the inequality that could be used to solve the following problem.
Three times a number is at most negative six.

Answers
Answer:
3x ≤ -6
Step-by-step explanation:
"At most" means "less than or equal to." If x represents the number, then you have ...
(three) times (a number) (is at most) negative 6 . . . . . English
3 · x ≤ -6 . . . . . . . . . . . . . . . . Math
__
3x ≤ -6
Answer:
3x ≤ -6
Step-by-step explanation:
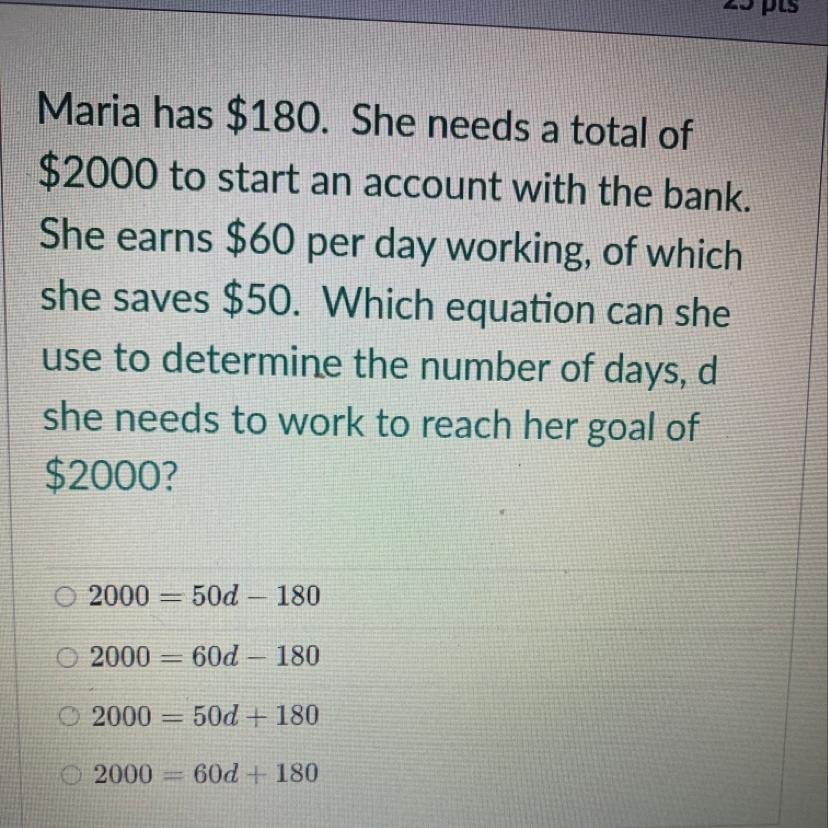
Maria has $180. She needs a total of
$2000 to start an account with the bank.
She earns $60 per day working, of which
she saves $50. Which equation can she
use to determine the number of days, d
she needs to work to reach her goal of
$2000?
Answers
Answer:
C (The one before the last one)
Step-by-step explanation:
2000 = 180 + 50d
She already has 180
Plus the $50 she saves each day (d)
2000 is the goal, or what we want it to equal.
In a five-card poker hand, what is the probability of being dealt exactly one four and no picture cards?
Answers
The probability of being dealt exactlu one four and no picture cards is 0.0907
What is probability?Probability is the study of the chances of occurrence of a result, which are obtained by the ratio between favorable cases and possible cases.
What is the probability in this case?Each deck has four suits, each of which contains three picture cards. Consequently, a deck of 52 playing cards has a total of 12 picture cards.
Now, in the whole deck, we will have four 4's. Thus, there are 52 − 12 − 4 = 36 cards that are neither 4's nor picture cards.
Number of ways to get 5-card poker hand = 4 X ³⁶C₄ = 235620 ways.
Number of ways for obtaining random 5 cards hands = ⁵²C₅ = 2598960 ways
Therefore, the probability of being dealt exactly one four and no picture cards = 235620 / 2598960 = 0.0907
Learn more about Probability here:brainly.com/question/25870256
#SPJ1
An amount of Birr 500 is deposited in an account at the end of each six-month period with an interest computed at 6% compounded semi-annually. How many years does it take for the amount to reach Birr 56,398.43?
Answers
It would take approximately 17.12 years for the amount to reach Birr 56,398.43 with a deposit of Birr 500 at the end of each six-month period, compounded semi-annually at an interest rate of 6%.
To solve this problem, we can use the formula for compound interest:
A = P(1 + r/n)^(nt)
Where:
A = Final amount
P = Principal amount (initial deposit)
r = Annual interest rate (in decimal form)
n = Number of compounding periods per year
t = Number of years
In this case, the principal amount is Birr 500, the annual interest rate is 6% (or 0.06), and the interest is compounded semi-annually, so there are 2 compounding periods per year.
We need to find the number of years (t) it takes for the amount to reach Birr 56,398.43.
Let's substitute the given values into the formula and solve for t:
56,398.43 = 500(1 + 0.06/2)^(2t)
Divide both sides by 500:
112.79686 = (1 + 0.03)^(2t)
Take the natural logarithm of both sides to eliminate the exponent:
ln(112.79686) = ln(1.03)^(2t)
Using the property of logarithms, we can bring down the exponent:
ln(112.79686) = 2t * ln(1.03)
Now, divide both sides by 2 * ln(1.03):
t = ln(112.79686) / (2 * ln(1.03))
Using a calculator, we find t ≈ 17.12.
For more such question on interest. visit :
https://brainly.com/question/25720319
#SPJ8
Which of the following would you see on a circle graph?
OA. Percentages
OB. Bars
C. Points
OD. A y-axis
Answers
A, percentages
You would see percentages on a circle graph, because it's how many parts of the whole that they take up.
Happy to help, have a great day! :)
2
Now comes the really tricky part. Can you come up with
your own magic square? You have to use positive and
negative numbers. Go ahead, earn your E and impress
me!
Drawo add image here
Magic Number =
Answers
Answer:here you go please and thankful
Step-by-step explanatio
How many cartwheels can Suzy do? :)
Answers
Answer:
100 :)
Step-by-step explanation:
Answer:
1
Step-by-step explanation:
Please help do this

Answers
Answer:
1)m+5q=1+5x5 =262)(y-x^3)=3-1^3 =3-1 =23)q(p+2)=3(3+2) =3(5) =154)y+y-x=5+5-6 =10-6 =45)(z+y)÷6=6+6÷6 =26)h(j-h)=3(6-3) = 3x3=97)x+y+y = 5+2+2=98)z^2-y =9-4=59)b(4+a)=2(4+6) =2x10 =2010)m-n+m =5-1+5 = 4+5 =911)(h+j)÷6 = (2+4)÷6 = 1mark as brainliast plzSelect all that apply

Answers
Answer: integer and rational
Step-by-step explanation:
Jenny won a charity raffle. Her prize will be randomly selected from the 9 prizes shown below. The prizes include 4 rings, 3 cameras, and 2 headsets.
Prizes
(a) Find the odds against Jenny winning a headset.
(b) Find the odds in favor of Jenny winning a headset.
Answers
The odds against Jenny winning a headset are 88.89% or 8 out of 9, and the odds in favor of Jenny winning a headset are 11.11% or 1 out of 9.
Since Jenny won a charity raffle, and her prize will be randomly selected from the 9 prizes shown below, and the prizes include 7 rings, 1 camera, and 1 headset, to find the odds against Jenny winning a headset, and find the odds in favor of Jenny winning a headset, the following calculations must be performed:
· 1 headset out of 9 total prizes
· 1/9 = headset
· 1/9 x 100 = 11.11%
· 100 - 11.11 = 88.89%
Therefore, the odds against Jenny winning a headset are 88.89% or 8 out of 9, and the odds in favor of Jenny winning a headset are 11.11% or 1 out of 9.
BONUS
Rectangle ABCD is shown on the coordinate grid below. What is the length of
diagonal AC?
Round to the nearest tenth.
B
A
D

Answers
Since A^2 +B^2 = C^2, 16+49= C^2
That means C^2 is 65, so you have to take the square root of 65.
Answer: AC= √65
A) Find an equation for the line perpendicular to the tangent line to the curve y=x^3-4x+6 at the point (2,6)
-The equation is y=
b) What is the smallest slope on the curve? At what point on the curve does the curve have this slope?
-The smallest slope on the curve is
-The curve has the smallest slope at the point
c) Find equations for the tangent lines to the curve at the points where the slope of the curve is 8.
Answers
Answer:
f(x) = x³ - 4x + 6
f'(x) = 3x² - 4
a) f'(2) = 3(2²) - 4 = 12 - 4 = 8
6 = 8(2) + b
6 = 16 + b
b = -10
y = 8x - 10
b) 3x² - 4 = 0
3x² = 4, so x = ±2/√3 = ±(2/3)√3
= ±1.1547
f(-(2/3)√3) = 9.0792
f((2/3)√3) = 2.9208
c) 3x² - 4 = 8
3x² = 12
x² = 4, so x = ±2
f(-2) = (-2)³ - 4(-2) + 6 = -8 + 8 + 6 = 6
6 = -2(8) + b
6 = -16 + b
b = 22
y = 8x + 22
f(2) = 6
y = 8x - 10
The equation perpendicular to the tangent is y = -1/8x + 25/4
-The smallest slope on the curve is 2.92
The curve has the smallest slope at the point (1.15, 2.92)
The equations at tangent points are y = 8x + 16 and y = 8x - 16
Finding the equation perpendicular to the tangentFrom the question, we have the following parameters that can be used in our computation:
y = x³ - 4x + 6
Differentiate
So, we have
f'(x) = 3x² - 4
The point is (2, 6)
So, we have
f'(2) = 3(2)² - 4
f'(2) = 8
The slope of the perpendicular line is
Slope = -1/8
So, we have
y = -1/8(x - 2) + 6
y = -1/8x + 25/4
The smallest slope on the curveWe have
f'(x) = 3x² - 4
Set to 0
3x² - 4 = 0
Solve for x
x = √[4/3]
x = 1.15
So, we have
Smallest slope = (√[4/3])³ - 4(√[4/3]) + 6
Smallest slope = 2.92
So, the smallest slope is 2.92 at (1.15, 2.92)
The equation of the tangent lineHere, we set f'(x) to 8
3x² - 4 = 8
Solve for x
x = ±2
Calculate y at x = ±2
y = (-2)³ - 4(-2) + 6 = 6: (-2, 0)
y = (2)³ - 4(2) + 6 = 6: (2, 0)
The equations at these points are
y = 8x + 16
y = 8x - 16
Read more about tangent lines at
https://brainly.com/question/21595470
#SPJ1
please help me find the rule for this table:
0,1
1,3
2,6
3,10
4,15
5,21
Answers
the first number in the first bracket is one lesser than the one we n the second bracket but the second one in the first bracket is one number bigger than the other.
Lisa makes 35 dollars per month babysitting . She spends 25% of what she earns on entertainment. How much does she spend on entertainment.
1. 4.50$
2. 8.75$
3. 10.00
4. 25.00$
Answers
find four consecutive whole numbers whose sum is 74
Answers
Answer:
17, 18, 19, 20
Explanation:
Let the numbers be x, x + 1, x + 2, x + 3
Their sum is equals to 74
x + x + 1 + x + 2 + x + 3 = 74 (group the variables)
x + x + x + x + 1 + 2 + 3 = 74 (simplify)
4(x) + 6 = 74 (subtract both sides by 6)
4x = 68 (divide both sides by 4)
x = 17
Other numbers:
x + 1 = 17 + 1 = 18
x + 2 = 17 + 2 = 19
x + 3 = 17 + 3 = 20
Answer:
17, 18, 19, 20
Step-by-step explanation:
Let four consecutive whole numbers be x, (x + 1), (x + 2) and (x + 3)According to the given condition:x + (x + 1) + (x + 2) + (x + 3) = 74-> 4x + 6 = 74-> 4x = 74 - 6-> 4x = 68-> x = 68/-> x = 17-> x + 1 = 17 + 1 = 18-> x + 2 = 17 + 2 = 19-> x + 3 = 17 + 3 = 20Thus, the four consecutive whole numbers are 17, 18, 19 and 20Please answer this correctly without making mistakes
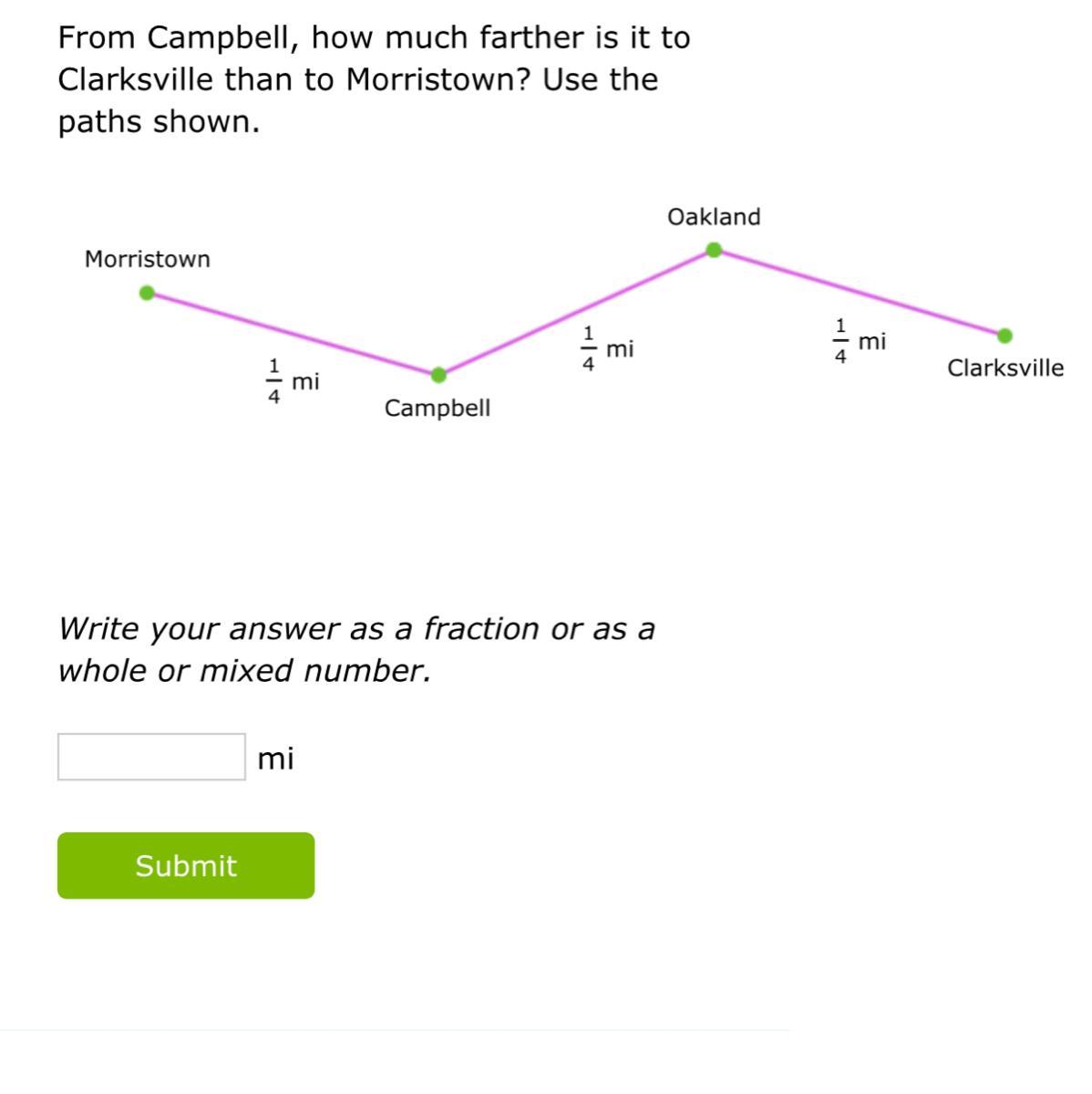
Answers
Answer:
1/4 miles
Step-by-step explanation:
Hey there!
Well starting at Campbell and going to Morristown it is 1/4 miles.
Going from Campbell to Clarksville it is 2/4 miles.
So to find the difference we’ll subtract.
2/4 - 1/4
= 1/4 miles
Hope this helps :)
Solve for x.
37°
8 cm
x = [?] cm
X
Round to the nearest hundredth.
X
![Solve for x.378 cmx = [?] cmXRound to the nearest hundredth.X](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/5r3s734YNpMZhrSKBRqrQYrII2vYUjgx.png)
Answers
The measure of side length x in the right triangle is approximately 6.03 cm.
What is the measure of side length x?The figure in the image is a right triangle having one of its interior angle at 90 degrees.
From the figure:
Angle θ = 37 degrees
Adjacent to angle θ = 8 cm
Opposite to angle θ = x
To solve for the missing side length x, we use the trigonometric ratio.
Note that: tangent = opposite / adjacent
Hence:
tan( θ ) = opposite / adjacent
Plug in the given values and solve for x:
tan( 37 ) = x / 8
x = tan( 37 ) × 8
x = 6.03 cm
Therefore, the value of x is 6.03 cm.
Learn more about trigonometric ratio here: brainly.com/question/28016662
#SPJ1
Amy, Tyrone, Nina, jake and Mandy are standing in line at the Grocery Store. Each has a different color shirt: red, green orange, blue and purple. Use following to answer.
Tyrone and Nina have only two people standing between them. The person wearing the orange shirt is not standing next to Mandy or Nina. Jake is wearing green. Mandy is in line at some point after Jake. The person wearing purple is either 2nds or 4th in line. Nina and Mandy are standing next to each other. Mandy is not wearing red. The person wearing the orange shirt is first in line. Tyrone is standing next to the person wearing green. Amy cannot be 1st or last in line.
Who is wearing purple shirt.
Answers
Answer:
Nina is wearing purple shirt.
Step-by-step explanation:
From the given information:
Mindy and Nina are one after another.
Tyrone is standing next to Jack who is wearing Green.
Now, between Tyrone and Nina, there are exactly two persons.
Combination of Tyrone and Nina can be either in the first four positions or last four positions as they have persons in between.
From the observation, Tyrone can be at the last position and Jake will be ahead of him. This is because Jake is ahead of Tyrone and he is wearing green and if Tyrone is at the second position then, there is no place for Jake as the first person is wearing orange.
So, at the fourth and fifth position, Jack and Tyrone are present.
Now, Nina must be at 2ns position because between Tyrone and Nina there should be 2 persons.
Amy can never be at 1st or last and hence, she will be at the 3rd position.
So, in first position Mandy will be present.
Now, 2nd or 4th person could wear purple, but in 4th position Jake is present who is wearing green
Thus, Nina at the second position should be wearing purple.
Fore more details, refer the link:
https://brainly.com/question/16679200?referrer=searchResults
Sets A and I are defined as follows. A = { − 1 , 0 , 1 , 2 , 4 , 6 , 7 } I = { − 2 , − 1 , 1 , 2 , 8 } Find the intersection of A and I
Answers
==========================================================
Explanation:
Start with set A and circle any value that you find in set I. Those values are -1, 1, and 2. These elements are found in both sets at the same time, hence they are in the intersection of set A and set I
Refer to the Venn diagram below. We have the values -1, 1, and 2 in the blue overlapped region. A value like 4 is only found in set A, so it's inside circle A, but outside circle I. On the flip side, a value like 8 is found outside of circle A but inside circle I.
The use of curly braces in the answer tells the reader we're dealing with a set of values. The order doesn't matter for any given set. Often it's helpful to put it in order from smallest to largest.

Which is equivalent to (2 × 5)^4
Answers
Answer:
32/40
Step-by-step explanation:
4x8 and 4x10
what mathematical strenght and skills did you develop in this lesson
Answers
Answer:
I have learned a lot in math, although it was years ago on of my favorite things to learn was to multiply and divide. They were not only easy but also fun.
Step-by-step explanation:
The range is the set of________
A) First Coordinates
B) Ordered Pairs
C) Second coordinates
Answers
Answer:
The range is the set of first coordinates
Benjamin threw a rock straight up from a cliff that was 60 ft above the water. If the height of the rock h, in feet, after t seconds is given by the equation h=-16t^2+68t+60, how long will it take for the rock to hit the water?
Answers
Answer:
5 sec
Step-by-step explanation:
Hit the water, means h = 0
Solve -16t^2 + 68t +60 =0
4t^2 - 17t - 15 = 0
(4t + 3)(t - 5) = 0
so t = 5 sec
The chance of rain is 20%, the chance of it being sunny is 60%, and the chance of it
being sunny and rainy at the same time is 10%. Calculate, the probability that it is
either sunny or rainy.
Answers
Answer:
0.6 = 60% probability that it is either sunny or rainy.
Step-by-step explanation:
We solve this question treating these events as Venn probabilities.
I am going to say that:
Event A: Rain
Event B: Sun
The chance of rain is 20%
This means that \(P(A) = 0.2\)
The chance of it being sunny is 60%
This means that \(P(B) = 0.6\)
The chance of it being sunny and rainy at the same time is 10%.
This means that \(P(A \cap B) = 0.1\)
Calculate, the probability that it is either sunny or rainy.
This is:
\(P = P(A) + P(B) - 2P(A \cap B) = 0.2 + 0.6 - 0.2 = 0.6\)
0.6 = 60% probability that it is either sunny or rainy.
A convex lens with focal length f centimeters will project the image of an object on a
point behind the lens. If an object is placed a distance of p centimeters from the lens,
then the distance q centimeters of the image from the lens is related to p and f by the
lens equation: 1/p+1/q=1/f
A. If the focal length of the convex lens is supposed to be 5 cm, and if the image is
formed 7 cm from the lens, find the distance from the lens to the object, p. (It’s not necessary to simplify your answer.)
B. Find an expression that gives q as a function of p, assuming that the focal length is a constant of 5 centimeters.
C. Sketch a graph of q as a function of p (i.e., q(p)), assuming that the focal length is a
constant of 5 centimeters. Show any important features of the graph.
D. Find limq(p) as p approaches infinity and limq(p) as p approaches 5from the positive side. What do these limits represent physically? What must
happen to the distance of the image and the object?
Answers
Answer:
A. Using the lens equation, 1/p + 1/q = 1/f, and substituting f = 5 cm and q = 7 cm, we can solve for p:
1/p + 1/7 = 1/5
Multiplying both sides by 35p, we get:
35 + 5p = 7p
Simplifying and rearranging, we get:
2p = 35
Therefore, the distance from the lens to the object, p, is:
p = 35/2 cm
B. Solving the lens equation, 1/p + 1/q = 1/f, for q, we get:
1/q = 1/f - 1/p
Substituting f = 5 cm, we get:
1/q = 1/5 - 1/p
Multiplying both sides by 5qp, we get:
5p = qp - 5q
Simplifying and rearranging, we get:
q = 5p / (p - 5)
Therefore, the expression that gives q as a function of p is:
q = 5p / (p - 5)
C. Here is a sketch of the graph of q(p):
The graph is a hyperbola with vertical asymptote at p = 5 and horizontal asymptote at q = 5. The image distance q is positive for object distances p greater than 5, which corresponds to a real image. The image distance q is negative for object distances p less than 5, which corresponds to a virtual image.
D. Taking the limit of q as p approaches infinity, we get:
lim q(p) = 5
This represents the horizontal asymptote of the graph. As the object distance becomes very large, the image distance approaches the focal length of the lens, which is 5 cm.
Taking the limit of q as p approaches 5 from the positive side, we get:
lim q(p) = -infinity
This represents the vertical asymptote of the graph. As the object distance approaches the focal length of the lens, the image distance becomes infinitely large, indicating that the lens is no longer able to form a real image.
In order for the lens to form a real image, the object distance p must be greater than the focal length f. When the object distance is less than the focal length, the lens forms a virtual image.
What is the solution set for this inequality?
15 < -3m -9
Answers
Answer:
15= -3m-9
15+9 = -3m
24 = -3m
-8= m
Therefore the m value is -8
23. Evaluate a(b + c) if a = 2, b = 3, and c = 4.
Simplify:
Answers
The value of the expression a(b + c) when a = 2, b = 3, and c = 4 is 14.
What is the value of the expression a(b + c) if a = 2, b = 3, and c = 4?Given the expression in the question:
a( b + c )
Also, a = 2, b = 3, and c = 4
To evaluate the expression a( b + c ) when a = 2, b = 3, and c = 4, we substitute these values into the expression:
Hence:
a( b + c )
Plug in a = 2, b = 3, and c = 4
2( 3 + 4 )
First, we simplify the parentheses by adding 3 and 4:
2( 7 )
Next, we multiply 2 and 7:
14
Therefore, the value of a(b + c) is 14 .
Learn more about algebraic expressions here: https://brainly.com/question/28959918
#SPJ1
info about the problems: I need the solved in y=mx+b form, and I need work showed in detail. thanksx +6y =187x + 14y =21- 3x - 4y =1212x - y =16
Answers
1.
\(x+6y=18\)\(6y=18-x\)\(y=-\frac{1}{6}x+3\)2.
\(7x+14y=21\)\(14y=-7x+21\)\(y=-\frac{1}{2}x+\frac{3}{2}\)3.
\(-3x-4y=12\)\(4y=-3x-12\)\(y=-\frac{3}{4}x-3\)4.
\(12x-y=16\)\(y=12x-16\)