By how many degrees did the temperature change overall?
Answers
Answer:
23
Step-by-step explanation:
because that is the answer I think
Answer:
23degrees
Step-by-step explanation:
Because that is what I think and l haven't learned much but I think it's 23 degrees
Related Questions
If i=-1 what is the value of i3?
-1
i
1
-i
Answers
Answer:
-i
Step-by-step explanation:
i^1=i
i^2=-1
i^3=-i
i^4=1
PLEASE ANDWER FAST
Sora is also making a salad. Her salad dressing recipe uses 6 teaspoons of vinegar for every 15
teaspoons of olive oil.
2.1 How much vinegar does Sora need for 5 teaspoons of olive oil?
2.2 How much olive oil does Sora need for 8 teaspoons of vinegar?
2.3 If Sora makes 42 teaspoons of salad dressing, how much of each ingredient is in it?
2.4 If Sora makes 14 teaspoons of salad dressing, how much of each ingredient is in it?
Answers
The following answers are given as:
2.1)
2 teaspoons of vinegar are needed for 5 teaspoons of olive oil.
2.2)
8 teaspoons of vinegar are needed for 20 teaspoons of olive oil.
2.3)
There are 12 teaspoons of vinegar and 30 teaspoons of olive oil in the 42 teaspoons of salad.
2.4)
There are 4 teaspoons of vinegar and 10 teaspoons of olive oil in the 14 teaspoons of salad.
What is a unit rate?It is the quantity of an amount of something at a rate of one of another quantity.
In 2 hours, a man can walk for 6 miles
In 1 hour, a man will walk for 3 miles.
We have,
6 teaspoons of vinegar = 15 teaspoons of olive oil.
1 teaspoon of vinegar = 5/2 teaspoons of olive oil.
Now,
1 teaspoon of vinegar = 5/2 teaspoons of olive oil.
Multiply 2 on both sides.
2 teaspoons of vinegar = 5 teaspoons of olive oil.
Now,
1 teaspoon of vinegar = 5/2 teaspoons of olive oil.
Multiply 8 on both sides.
8 teaspoons of vinegar = 20 teaspoons of olive oil.
Now,
Total number of teaspoons = 42
1 teaspoon of vinegar = 5/2 teaspoons of olive oil.
Multiply 12 on both sides.
12 teaspoons of vinegar = 30 teaspoons of olive oil.
12 + 30 = 42 teaspoons
Now,
1 teaspoon of vinegar = 5/2 teaspoons of olive oil.
Multiply 4 on both sides.
4 teaspoons of vinegar = 10 teaspoons of olive oil.
4 + 10 = 14 teaspoons
Thus,
2 teaspoons of vinegar are needed for 5 teaspoons of olive oil.
8 teaspoons of vinegar are needed for 20 teaspoons of olive oil.
There are 12 teaspoons of vinegar and 30 teaspoons of olive oil in the 42 teaspoons of salad.
There are 4 teaspoons of vinegar and 10 teaspoons of olive oil in the 14 teaspoons of salad.
Learn more about unit rates here:
https://brainly.com/question/11258929
#SPJ1
Someone please answer this correctly!!

Answers
Answer:
1.98 × 10^10
Step-by-step explanation:
First solve for how many text messages were sent out per one month:
22,000,000 × 900
19,800,000,000
Convert into scientific notation:
1.98 × 10^10
In scientific notation, there can only be one number before the decimal. The rest of the numbers must be after the decimal; hence, why I put the numbers 9 and 8 after the decimal. If the rest of the numbers are zeros, you do not have to add them after the decimal. Instead, starting from right to left, count the number places until you reach your decimal. The number you have counted will be your exponent. I counted nine 0's, one 8, and one 9 which made this exponent 10 as there were 10 decimal placements.
Solve the equation.
3y + 11 = -16
Answers
Answer:
y= -9
Step-by-step explanation:
Answer:
y = -9
Step-by-step explanation:
Algebra:
3y + 11 = -16
-11 -11
3y = -27
÷ 3 ÷ 3
y = -9
Determine whether each equation is true or false.
-5/-1 = 5
(0/-4) = 0
-3/1 = -3
- 8/0 = 0
Answers
Step-by-step explanation:
1.False
2.True
3.True
4.False
what is 4901 and 75 estimated to
Answers
on what scale? to the nearest what? Elaborations, PLEASE
Anyways it's just:
4901 (4900*) + 75 (80*) = 4980
*i'm guessing
BUT if they want you to round after addition:
the answer would be 5000
I've done every problem I only need with the help this problem

Answers
Answers:
\(\displaystyle \lim_{x \to 2^{+}} f(x) = 1\\\\\displaystyle \lim_{x \to 2^{-}} f(x) = 1\\\)
Both result in the same limit value. This allows us to say \(\displaystyle \lim_{x \to 2} f(x) = 1\) without the plus or minus over the 2.
The left and right hand limits may not always match like this.
==================================================
Explanation:
The notation \(\displaystyle \lim_{x \to 2^{+}} f(x)\) means that we are approaching x = 2 from the right hand side. This is from the positive direction. So we start at say x = 3 and move to x = 2.5 then to x = 2.1 then to x = 2.01 and so on.
Because we started with values x > 2, we will use the third definition of the piecewise function
if x > 2, then f(x) = 3x-5
Plug in x = 2 to get
f(x) = 3x-5
f(2) = 3(2)-5
f(2) = 6-5
f(2) = 1
This shows \(\displaystyle \lim_{x \to 2^{+}} f(x) = 1\)
-----------------------------
For the other limit, we're approaching x = 2 from the negative side. So we could start at say x = 0, then move to x = 1, then to x = 1.5 then to x = 1.9 then to x = 1.99, and so on.
We're using x values such that x < 2 now.
So we'll be using the first definition of the piecewise function
If x < 2, then f(x) = x^2 - 3
f(x) = x^2-3
f(2) = 2^2-3
f(2) = 4-3
f(2) = 1
We end up with \(\displaystyle \lim_{x \to 2^{-}} f(x) = 1\)
---------------------------------
Both right hand limit and left hand limit result in the same value
Because \(\displaystyle \lim_{x \to 2^{+}} f(x) = \displaystyle \lim_{x \to 2^{-}} f(x) = 1\)
We can shorten that to \(\displaystyle \lim_{x \to 2^{}} f(x) = 1\) meaning we can approach x = 2 from either direction to arrive at the same limiting value.
A thing to notice is that f(2) is not equal to 1. Instead the second line of the piecewise function says f(2) = 3.
The fact that the limit as x approaches 2 and f(2) don't agree means this function is not continuous at x = 2.
The graph shows this. We have a removable discontinuity where we effectively picked the point off the graph and move it upward.
See the diagram below.

Solve by Factoring:
2x^2 - x - 3 = 0
Answers
Answer:
x = 3/2 or x = -1
Step-by-step explanation:
2x² - x - 3 = 0
2*(-3) = -6
Factors of -6:
(-1, 6), (1, -6), (-2, 3), (2, -3)
We need to find a pair that adds up to the co-eff of x which is (-1)
Factors :(2,-3)
2 - 3 = -1
so, 2x² - x - 3 = 0 can be written as:
2x² + 2x - 3x - 3 = 0
⇒ 2x(x + 1) -3(x + 1) = 0
⇒ (2x - 3)(x + 1) = 0
⇒ 2x - 3 = 0 or
x + 1 = 0
⇒ 2x = 3 or x = -1
⇒ x = 3/2 or x = -1
i need help plz the question is in the image

Answers
Answer:
46<h
Hopes this helps :)
In ΔNOP, n = 56 inches, p = 61 inches and ∠P=80°. Find all possible values of ∠N, to the nearest degree.
Answers
The value of ∠N is 54.38 degrees.
Given that in ΔNOP, n = 56 inches, p = 61 inches and ∠P=80°.
We need to find the value of ∠N,
According to the cosine rule, the following equation is true for every triangle with sides a, b, and c and the corresponding opposite angles A, B, and C:
c² = 2ab cos(C) - a² + b²
In this instance, we have:
A = P and B = P
C = ∠P
When we enter the values, we obtain:
n² = p² + p² - 2p² cos(∠P)
Substituting the known values:
56² = 61² + 61² - 2(61²) cos(80°)
Simplifying:
3136 = 3721 + 3721 - 2(3721) cos(80°)
3136 = 3721 + 3721 - 7442 cos(80°)
Now we can solve for cos(80°):
3136 = 7442 - 7442 cos(80°)
7442 cos(80°) = 7442 - 3136
cos(80°) = (7442 - 3136) / 7442
cos(80°) ≈ 0.5798
∠N = arccos(0.5798)
∠N = 54.38 degrees.
Hence the value of ∠N is 54.38 degrees.
Learn more about cosine rule, click;
https://brainly.com/question/28716982
#SPJ1
If annual interest rate is 8.25% on 90,900.00 What is my interest for 1/2 a month. It's for 8 years.
Answers
To calculate the interest for 1/2 a month over a period of 8 years, we first need to calculate the total number of months in 8 years:
Total number of months = 8 years x 12 months/year = 96 months
Next, we can calculate the interest for half a month:
Interest = Principal x Rate x Time
Where:
- Principal = $90,900.00
- Rate = 8.25% (annual interest rate)
- Time = 0.5/12 years (half a month, expressed in years)
Rate needs to be converted to a monthly rate, so we divide it by 12:
Rate = 8.25% / 12 = 0.6875% (monthly interest rate)
Time needs to be expressed in years, so we divide it by 12:
Time = 0.5/12 years
Now we can calculate the interest:
Interest = $90,900.00 x 0.006875 x 0.0416667
Interest = $25.08 (rounded to the nearest cent)
Therefore, the interest for 1/2 a month on a principal of $90,900.00 with an annual interest rate of 8.25% over a period of 8 years is $25.08.
Answer:
The interest for 1/2 month is $312.47, and the total interest for 8 years is $30, 032.64
Step-by-step explanation:
Make a plan:
Monthly Interest Rate: 8.25% / 12 = 0.006875Interest for 1/2 month is 90900 * 0.006875 * 0.5 = 312.46875Total Interest for 8 years is 312.46875 * 8 * 12 = 30032.64Solve the problem:The monthly Interest Rate is 8.25% / 12 = 0.006875 (Ground Truth)Interest for 1/2 month is 90900 * 0.006875 * 0.5 = 312.46875 (ground truth).Total Interest for 8 years is 312.46875 * 8 * 12 = 30032.64 (ground truth).Draw the conclusion:
The interest for 1/2 month is $312.47, and the total interest for 8 years is $30, 032.64Hope this helps!
Evaluate the integral following

Answers
Answer:
\(\displaystyle{4\tan x + \sin 2x - 6x + C}\)
Step-by-step explanation:
We are given the integral of:
\(\displaystyle{\int 4(\sec x - \cos x)^2 \, dx}\)
First, we can use a property to separate a constant out of integrand:
\(\displaystyle{4 \int (\sec x - \cos x)^2 \, dx}\)
Next, expand the expression (integrand):
\(\displaystyle{4 \int \sec^2 x - 2\sec x \cos x + \cos^2 x \, dx}\)
Since \(\displaystyle{\sec x = \dfrac{1}{\cos x}}\) then it can be simplified to:
\(\displaystyle{4 \int \dfrac{1}{\cos^2 x} - 2\dfrac{1}{\cos x} \cos x + \cos^2 x \, dx}\\\\\displaystyle{4 \int \dfrac{1}{\cos^2 x} - 2 + \cos^2 x \, dx}\)
Recall the formula:
\(\displaystyle{\int \dfrac{1}{\cos ^2 x} \, dx = \int \sec ^2 x \, dx = \tan x + C}\\\\\displaystyle{\int A \, dx = Ax + C \ \ \tt{(A \ and \ C \ are \ constant.)}\)
For \(\displaystyle{\cos ^2 x}\), we need to convert to another identity since the integrand does not have a default or specific integration formula. We know that:
\(\displaystyle{2\cos^2 x -1 = \cos2x}\)
We can solve for \(\displaystyle{\cos ^2x}\) which is:
\(\displaystyle{2\cos^2 x = \cos2x+1}\\\\\displaystyle{\cos^2x = \dfrac{\cos 2x +1}{2}}\)
Therefore, we can write new integral as:
\(\displaystyle{4 \int \dfrac{1}{\cos^2 x} - 2 + \dfrac{\cos2x +1}{2} \, dx}\)
Evaluate each integral, applying the integration formula:
\(\displaystyle{\int \dfrac{1}{\cos^2x} \, dx = \boxed{\tan x + C}}\\\\\displaystyle{\int -2 \, dx = \boxed{-2x + C}}\\\\\displaystyle{\int \dfrac{\cos 2x +1}{2} \, dx = \dfrac{1}{2}\int \cos 2x +1 \, dx}\\\\\displaystyle{= \dfrac{1}{2}\left(\dfrac{1}{2}\sin 2x + x\right) + C}\\\\\displaystyle{= \boxed{\dfrac{1}{4}\sin 2x + \dfrac{1}{2}x + C}}\)
Then add all these boxed integrated together then we'll get:
\(\displaystyle{4\left(\tan x - 2x + \dfrac{1}{4}\sin 2x + \dfrac{1}{2} x\right) + C}\)
Expand 4 in the expression:
\(\displaystyle{4\tan x - 8x +\sin 2x + 2 x + C}\\\\\displaystyle{4\tan x + \sin 2x - 6x + C}\)
Therefore, the answer is:
\(\displaystyle{4\tan x + \sin 2x - 6x + C}\)
please assist with these questions thanks



Answers
1a. The percentage total return is -19.56%
1b. The dividend yield is 2.42%.
1c. The capital gains yield is -21.98%.
2a. The arithmetic average annual return on large-company stocks in nominal terms is 14.5%.
2b. The arithmetic average annual return on large-company stocks in real terms is 9.67%.
3a. The real return on long-term government bonds is 3.195%
3b. The real return on long-term corporate bonds is 3.291%
How to calculate the percentage total return?In Financial accounting, the percentage total return (P) can be calculated by using this formula;
P = [(Ending price - Initial price) + Dividend] ÷ Initial price
P = [(71 - 91) + 2.20] ÷ 91
P = -0.1956 or -19.56%
1b. For the dividend yield, we have:
Dividend yield = Dividend ÷ Initial price
Dividend yield = 2.20 ÷ 91
Dividend yield = 0.0242 or 2.42%
1c. For capital gains yield, we have:
Capital gains yield = (Ending price - Initial price) ÷ Initial price
Capital gains yield = (71 - 91) ÷ 91
Capital gains yield = -0.2198 or -21.98%.
Part 2.
a. The arithmetic average of annual return on large-company stocks in nominal terms is equal to 14.5%.
b. For arithmetic average annual return in real terms, we have:
(1 + 0.145) = (1 + r)(1 + 0.044)
r = (1.145/1.044) - 1
r = 9.67%
Part 3.
a. For real return on the long-term government bonds, we would apply Fisher equation:
(1 + i) = (1 + r)(1 + h)
Where:
i is the nominal interest rate.r is the real interest rate.h is the inflation rate.(1 + 0.066) = (1 + r)(1 + 0.033)
1 + r = 1.066/1.033
r = 3.195%
b. For real return on long-term corporate bonds:
(1 + 0.067) = (1 + r)(1 + 0.033)
1 + r = 1.067/1.033
r = 3.291%
Learn more about real return and stocks here: https://brainly.com/question/32228847
#SPJ1
A farmer plants the same amount every day, adding up to 2 1/4 acres at the end of the year. If the year is 3/4 over, how many acres has the farmer planted?
Answers
Answer:
9/4 * 3/4 = 27/16 = 1 \(\frac{9}{16}\)
Step-by-step explanation:
The price to go to a show is usually $16.50, but if you go on Tuesday, you will only pay $9.90.
What percent of the original price is the discounted ticket price?
Answers
A rocket is launched in the air. Its height in feet is given by h (t) = -16t^2 + 104t where t represents the time in seconds after launch. What is the appropriate domain for this situation?
Answers
Looking at the function h(t), it is a polynomial function.
The domain of this type of function usually is all real numbers.
But in this case, since the independent variable t represents the time, its value can't be negative, it usually starts at t = 0.
Therefore the appropriate domain for this situation is all non-negative numbers:
\(\begin{gathered} t\geq0\\ \\ or\\ \\ \text{ }[0,\infty) \end{gathered}\)I need help with this please
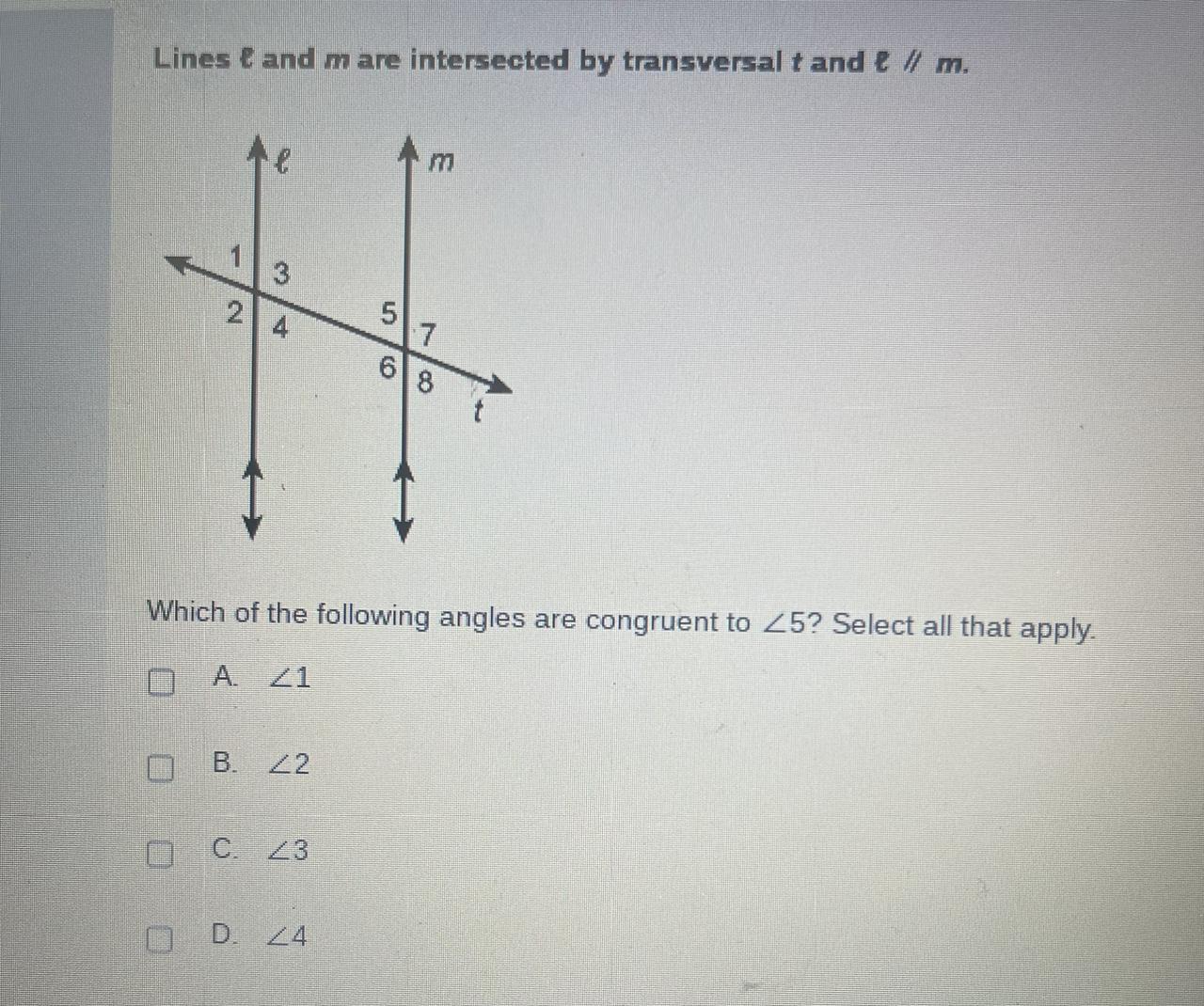
Answers
Answer:
<4 (D)
Step-by-step explanation:
it is the same angle :D
also can you please help me??
What is the surface area of the image below?

Answers
Answer:
Step-by-step explanation:
Comment
I'm going to assume that this is not a closed figure. The top is open like a water trough for horses.
There are 2 semicircular ends which add up to 1 whole circle.
There is 1 base area. The base area has a width of one of the semicircles. It has a length of 15 cm.
Solution
2 semi circles
r = d / 2
r = 20/2
r = 10
Area = pi r^2 This area is for 2 semicircles which = 1 circle.
Area = 3.14 * 10^2
Area = 3.14 * 100
Area = 314
Trough
r = d / 2
d= 20
r = 20/2
r= 10
w = 2*pi*r / 2
w = 2*3.14 *10/2
w = 31.4 cm
L = 15 cm
Area = 15 * 31.4
Area = 471
Total Area = 785
Mark walked 12 1/2 miles in 5 hours. How many miles did Mark walk in 1 hour?
Answers
the answe is it is 2.5 or 2 1/2 as he said but in conclusion answe 2 1/2 or 2 and 1 half
Distance can be defined as how far a person or an object can go or cover.
The number of miles Mark walked in 1 hour is \(2\frac{1}{2}\) miles
From the question,
In 5 hours, Mark walked a distance of 12 1/2 miles.
Hence,
5 hours = \(12\frac{1}{2}\) miles
1 hour = ?
Cross Multiply
1 hour x \(12\frac{1}{2}\) miles / 5 hours
= \(2\frac{1}{2}\) miles
The number of miles Mark walked in 1 hour is \(2\frac{1}{2}\) miles
To learn more, visit the link below:
https://brainly.com/question/8805976
suppose the functions u and w are defined as follows u(x)=x+9 w(x)=the square root of x+8 find the following (wou)(8)= (uow)(8)=
Answers
Answer:
5 and 13
Step-by-step explanation:
To evaluate (w ○ u)(8) , evaluate u(8) then substitute the value obtained into w(x) , that is
u(8) = = 8 + 9 = 17 , then
w(17) = \(\sqrt{17+8}\) = \(\sqrt{25}\) = 5
---------------------------------------
To evaluate (u ○ w )(8) , evaluate w(8) then substitute the value obtained into u(x) , that is
w(8) = \(\sqrt{8+8}\) = \(\sqrt{16}\) = 4 , then
u(4) = 4 + 9 = 13
Answer:
Step-by-step explanation:
\(u(x)=x+9\\\\w(x)=\sqrt{x+8} \\\\(wou)(x)=u(w(x))=u(\sqrt{x+8} )=\sqrt{x+8}+9\\(wou)(8)= \sqrt{8+8}+9=4+9=13\\\\\\(uow)(x)=w(u(x))=w(x+9)=\sqrt{x+9+8}=\sqrt{x+17}\\(wou)(8)= \sqrt{8+17}=\sqrt{25}=5\\\\\)
Nelson lands 4650 on 2% interest rate. He plans to pay this after 2 months. What will the total principal and interest payment be?
Answers
The total principal and interest payment that Nelson will have to pay after 2 months is $4665.50.
To calculate the total principal and interest payment, we need to determine the interest amount and add it to the principal.
First, let's find the interest amount:
Interest = Principal x Interest Rate x Time
Given:
Principal = $4650
Interest Rate = 2% per year
Time = 2 months
Since the interest rate is given on an annual basis, we need to convert the time from months to years. There are 12 months in a year, so 2 months is equivalent to 2/12 = 1/6 years.
Interest = $4650 x 0.02 x (1/6) = $15.50
Now, we can calculate the total principal and interest payment:
Total Payment = Principal + Interest
Total Payment = $4650 + $15.50 = $4665.50
For more such questions on principal visit:
https://brainly.com/question/25720319
#SPJ8
is 141.3 more than 141.05
Answers
Answer:
Yes
Step-by-step explanation:
Since the base numbers (141) is the same, we can ignore that.
Now, let's look at .3 and .05.
.3 is the same as .30.
If we remove the decimal point, we're looking at 30 and 5. 30 is greater than 5, so 141.3 is greater than 141.05.
The company also wants to offer a family size box of cereal. The family size box will be a dilation of the single serving 1.2-ounce box. It must contain 18.75 ounces of cereal. What scale factor does the company need to use for the family size box? Explain or show your reasoning.
Answers
the size factor will be 2.5.
What is dilation?Through a modification known as dilation, an object can be resized. By dilatation, the objects can be resized or enlarged. This transformation results in a shape that is a perfect replica of the original image. The form's dimensions do vary, though. An expansion or contraction of the original form is required for a dilatation. This shift is referred to as the scale factor.
The size disparity between the new and old photos is referred to as the scaling factor. The centre of dilatation is a fixed point in the plane. The scale factor and the centre of dilation determine the dilation transformation.
Given that the box has been enlarged by a scale factor of 4, its length, width, and volume have all been increased by 4 times from their original values.
as a result, it has dilated to 72.68
The volume of the box is dilated by a scale factor of 2.5 because the beginning amount of cereal was 12 ounces and the final amount was 18.75 ounces.
Hence the size factor will be 2.5.
Learn more about dilation, by the following link
https://brainly.com/question/13176891
#SPJ1
8.2'
Given conversion factor
12 in
1 ft
measure in inches? Round your answer to the nearest tenth.
what is the above line segment's unit of
Answers
Answer:
98.4
Step-by-step explanation:
Solve
make B the subject of formula
\(A = \frac{1}{2} bh\)
After making B the subject of formula
find b when A = 135 , H = 18
Answers
Step-by-step explanation:
A = 1/2 × B × H
transform to have B = ...
A/H = 1/2 × B
B = 2 × A/H
B = 2 × 135/18 = 135/9 = 15
Cecilia simplified an expression. Her work is shown below.
(6 and one-half + 2 and three-fourths) minus 1.5 times (4.5 divided by 0.5)
Step 1 9 and one-fourth minus 1.5 times (4.5 divided by 0.5)
Step 2 7.75 times (4.5 divided by 0.5)
Step 3 7.75 times 9
Step 4 69.75
Where did Cecilia make her first mistake?
step 1
step 2
step 3
step 4
Answers
Answer: second step.
Step-by-step explanation:
you then have to distribute the answer not subtract 9 1/4 from 1.5
you have to do the parenthesis next
4.5/0.5=45/5=9
then
1.5*9= 13.5
then
9.25-13.5 which I think you are capable of solving
Answer:
Step 2Step-by-step explanation:
Given work on simplification
(6 and one-half + 2 and three-fourths) minus 1.5 times (4.5 divided by 0.5) (6 1/2 + 2 3/4) - 1.5 (4.5 ÷ 0.5)Step 1 9 and one-fourth minus 1.5 times (4.5 divided by 0.5)
9 1/4 - 1.5 (4.5 ÷ 0.5)This is ok as first step is solving parenthesisStep 2 7.75 times (4.5 divided by 0.5)
7.75 (4.5 ÷ 0.5)Incorrect, subtraction should be the last stepDetermine the average rate of change of this function over the interval -2≤x≤4
Answers
The rate of change of the function h(x) = 2x on the interval 2 ≤ x ≤ 4 is 6.
For each statement, write what would be assumed and what would be proven in a proof by contrapositive of the statement. Then write what would be assumed and what would be proven in a proof by contradiction of the statement.
a. If x and y are a pair of consecutive integers, then x and y have opposite parity.
b. For all integers n, if n² is odd, then n is also odd.
Answers
Answer:
a)
Given Statement - If x and y are a pair of consecutive integers, then x and y have opposite parity.
Proof by Contrapositive:
Assumed statement: Suppose that integers x and y do not have opposite parity.
Proven Statement: x and y are not a pair of consecutive integers.
Proof -
x = 2u₁ , y = 2u₂
Then
(x, x+1) = (2u₁ , 2u₁ + 1) = (Even, odd)
If y = 2u₁ + 1
Not possible
⇒x and y are not a pair of consecutive integers.
Hence proved.
Proof by Contradiction:
Assumed statement: Suppose x and y are not a pair of consecutive integers.
Proven Statement: Suppose x and y do not have opposite parity.
Proof -
If x and y are not a pair of consecutive integers.
⇒ either x and y are odd or even
If x and y are odd
⇒x and y have same parity
Contradiction
If x and y are even
⇒x and y have same parity
Contradiction
(b)
Proof by Contrapositive:
Assumed statement: Let n be an integer such that n is not odd (i.e. n is an even integer)
Proven Statement: n² is not odd (i.e n² is even)
Proof -
Let n is even
⇒n = 2m
⇒n² = (2m)² = 4m²
⇒n² is even
Hence proved.
Proof by Contradiction:
Assumed statement: Let n be an integer such that n² be odd.
Proven Statement: suppose that n is not odd (i.e n is even)
Proof -
Let n² is odd
⇒n² is even
⇒n² = 2m
⇒2 | n²
⇒2 | n
⇒n = 2x
⇒ n is even
Contradiction
The product of 4 and the difference of a number and 7.
Answers
Answer:
simplified: 4x−28
Step-by-step explanation:
The product of 4 and the difference of a number and 7 can be written as 4(x-7) where x is the number you are looking for.
Collect data on the OBSERVATION table in ANNEXURE A to record 30 days of the minimum and maximum temperature in your community. Arrange the maximum temperature of the 30 days in ascending order to summarize the data. Determine the mean, mode, median, and range. Use the maximum temperature data and draw for each section a frequency table with appropriate intervals in ANNEXTURE B Display or represent the data from the frequency table on a pie chart in ANNEXTURE B. First, calculate the size of the angles for the pie chart. Example: Intervals between 20-30 are 5. Therefore the proportion of the Segment: 11 [360° = 72° Show all your calculations. 11 Which data collection best describe the maximum and why?
Answers
Answer:
I do not have access to Annexure A and Annexure B, so I cannot collect the data, draw the frequency table or pie chart, or answer the last question. However, I can provide a general explanation of how to calculate the mean, mode, median, and range from a set of data.
To find the mean (average) of a set of data, add up all the values in the set and divide by the number of values. For example, if the maximum temperatures of the 30 days are:
25, 28, 29, 27, 26, 30, 31, 32, 29, 27, 26, 24, 23, 25, 28, 30, 32, 33, 34, 31, 29, 28, 27, 26, 25, 24, 23, 21, 20, 22
The sum of the values is:
25 + 28 + 29 + 27 + 26 + 30 + 31 + 32 + 29 + 27 + 26 + 24 + 23 + 25 + 28 + 30 + 32 + 33 + 34 + 31 + 29 + 28 + 27 + 26 + 25 + 24 + 23 + 21 + 20 + 22 = 813
Dividing by the number of values (30), we get:
Mean = 813/30 = 27.1
To find the mode of a set of data, identify the value that occurs most frequently. In this example, there are two values that occur most frequently, 27 and 29, so the data has two modes.
To find the median of a set of data, arrange the values in order from smallest to largest and find the middle value. If there are an even number of values, take the mean of the two middle values. In this example, the values in ascending order are:
20, 21, 22, 23, 23, 24, 24, 25, 25, 26, 26, 27, 27, 27, 28, 28, 29, 29, 29, 30, 30, 31, 31, 32, 32, 33, 34
There are 30 values, so the median is the 15th value, which is 28.
To find the range of a set of data, subtract the smallest value from the largest value. In this example, the smallest value is 20 and the largest value is 34, so the range is:
Range = 34 - 20 = 14
To create a frequency table for the maximum temperature data, we need to group the data into intervals and count the number of values that fall into each interval. For example, we could use the following intervals:
20-24, 25-29, 30-34
The frequency table would look like this:
Interval | Frequency
20-24 | 4
25-29 | 18
30-34 | 8
To calculate the size of the angles for the pie chart, we need to find the total frequency (30) and divide 360° by the total frequency to get the proportion of each interval in degrees. For example, for the interval 25-29:
Proportion = Frequency/Total frequency = 18/30 = 0.6
Angle = Proportion * 360° = 0.6 * 360° = 216°
We can repeat this calculation for each interval to obtain the angles for the pie chart.
In terms of the last question, it is not clear what is meant by "which data collection best describe the maximum and why?". If you could provide more context or clarification, I would be happy to try to help.