consider the table below.which of the following squares root equation best fits the data in the table?

Answers
Answer
Option D is the answer.
y = 0.19 √[120 (x + 2.29)]
Explanation
We are asked to find the function that fits the data in the table.
To do this, we will need to check some of these functions by putting the values in the table in it and seeing if they fit
Option A
y = 0.29 √[110 (x + 1.95)]
when x = -2, y = 1
y = 0.29 √[110 (-2 + 1.95)]
y = 0.29 √[110 (-0.05)]
y = 0.29 √[-5.5]
Since there isn't a real number square root for negative numbers, there is no value for y when x = -2
Option A cannot be the answer.
Option B
y = 0.25 √[130 (x + 2.5)]
when x = -2, y = 1
y = 0.25 √[130 (-2 + 2.5)]
y = 0.25 √[130 (0.5)]
y = 0.25 √[65]
y = 0.25 (8.1)
y = 2
2 ≠ 1
Option B is not the answer.
Option C
y = 0.37 √[115 (x - 2.14)]
when x = -2, y = 1
y = 0.37 √[115 (-2 - 2.14)]
y = 0.37 √[115 (-4.14)]
y = 0.37 √[-476.1]
Since there isn't a real number square root for negative numbers, there is no value for y when x = -2
Option C cannot be the answer.
Option D
y = 0.19 √[120 (x + 2.29)]
when x = -2, y = 1
y = 0.19 √[120 (-2 + 2.29)]
y = 0.19 √[120 (0.29)]
y = 0.19 √[34.8]
y = 0.19 (5.9)
y = 1.1 = 1
Since this is the only one that even the first value on the table fits, this has to be the only option that fits the data.
We can check the rest of the data for this too, but since all the other options failed the first test, it is clear that this option is the correct answer.
Hope this Helps!!!
Related Questions
HELP!
Aiden has a gross income of $63,000 and takes the standard deduction. Their total taxes due are $6,922.
Answers
Step-by-step explanation:
So it's really easy if you read it carefully, the only thing you need to do is 63,000 - 6,922 = _____ and that's it hope it helps
The side lengths of polygon A are 3,6,6 and 9 inches. Polygon b is a scaled copy of a whose shortest side is 2 inches long. What are the other side lengths of polygon B
Answers
Answer:
2, 4, 4, 6
Step-by-step explanation:
So to get 3 to 2, you'd need to multiply by 2/3, so 2/3 would be the scale factor. 2/3*6=4, 9*2/3=6
A parabolic arch sculpture is on top of a city bank. A model of the arch is y = −0.005x2 + 0.3x where x and y are in feet.
The image is of a rectangle which represents the building of a Bank and its height is 30 feet. On top of it a semi circle is placed whose diameter is equal to the width of the rectangle.
a. What is the distance from the highest point of the arch to the ground?
b. What is the width of the bank?
A. a. 34.5 feet
b. 60 feet
B. a. 4.5 feet
b. 60 feet
C. a. 4.5 feet
b. 30 feet
D. a. 34.5 feet
b. 30 feet
Answers
Answer:
A. a. 34.5 feet
b. 60 feet
Step-by-step explanation:
Parabola equation
\(y=-0.005x^2+0.3x\)
Differentiating with respect to x we get
\(\dfrac{dy}{dx}=-0.01x+0.3\)
Equating with zero
\(-0.01x+0.3=0\\\Rightarrow -0.01x=-0.3\\\Rightarrow x=\dfrac{0.3}{0.01}\\\Rightarrow x=30\)
Double derivative of the parabolic equation
\(\dfrac{d^2y}{dx^2}=-0.01<0\)
So, \(x=30\) is maximum.
\(y=-0.005\times 30^2+0.3\times 30\\\Rightarrow y=4.5\)
So, the maximum height of the arch will be 4.5 feet.
From the ground the highest point of the arch will be \(30+4.5=34.5\ \text{ft}\)
We are taking the x axis as the width of the bank.
\(0=-0.005x^2+0.3x\\\Rightarrow 0.005x^2=0.3x\\\Rightarrow x=\dfrac{0.3}{0.005}\\\Rightarrow x=60\)
So, the width of the bank will be 60 feet.

6a - 3c + a + 2b = what the answer
Answers
Answer:
7a+2b-3c
Step-by-step explanation:
6a+a = 7a
2b stays the same
-3c stays the same
Answer:
Hey mate, here is your answer. Hope it helps you.
7a-3c+2b
Step-by-step explanation:
6a+a-3c+2b
=7a-3c+2b
3c and 2b will be the same because the variables are different. They are not like terms.
A poll of 826 students at alpha statue college found that 61% of those polled preferred a quarter system to a trimester system estimate a 95% confidence interval for the percentage of students who prefer a quarter system
Answers
To find the confidence interval, we use the following formula.
\(p\pm z\cdot\sqrt[]{\frac{p(1-p)}{n}}\)Where z = 1.96 for a 95% confidence interval. Replacing the given information, we have the following:
\(\begin{gathered} 0.61\pm1.96\cdot\sqrt[]{\frac{0.61(1-0.61)}{826}} \\ 0.61\pm1.96\cdot\sqrt[]{\frac{0.61(0.39)}{826}} \\ 0.61\pm1.96\cdot\sqrt[]{\frac{0.24}{826}} \\ 0.61\pm0.03 \end{gathered}\)So, the confidence interval is
\(\begin{gathered} (0.61-0.03;0.61+0.03) \\ (0.58;0.64) \end{gathered}\)The interval: (0.58 ; 0.64)Write an equivalent expression. 4x - x
Answers
Answer:
5x-2x
Step-by-step explanation:
4x-x = 3x
so,
5x-2x = 3x
The equivalent expression would be; 5x-2x
What are equivalent expressions?Those expressions who might look different but their simplified forms are same expressions are called equivalent expressions.
To derive equivalent expressions of some expression, we can either make it look more complex or simple. Usually, we simplify it.
We are given that the expression as; 4x - x
We need to find an equivalent expression.
Therefore, solving further;
4x-x = 3x
Thus, we can also create one expression as;
5x-2x = 3x
Learn more about expression here;
https://brainly.com/question/14083225
#SPJ2
Which of the following best describes the use of the formula S = (n - 2)180°,
where n is the number of sides?
A. It is used to find the number of interior angles in a regular polygon.
B. It is used to find the sum of the interior angles in a regular
polygon.
O c. It is used to find the sum of the exterior angles in a regular
polygon
O D. It is used to find the number of exterior angles in a regular
polygon
SUBMIT
Answers
a is a negative odd number.
Choose two words from the list in the box that describe a²
A negative
B positive
Codd
D even
Answers
Answer:
positive and odd
Step-by-step explanation:
If a is a negative odd number, then a² can't be negative, because a number squared is always positive.
I'll illustrate this with an example.
Let's choose -7 as an example. Instead of a.
-7² = 49
So we see that the result is positive & odd.
So the words that describe a^2 are positive and odd.
0 is an angle in a right-angled triangle. tan 0 = 23/52 What is the value of 0? Give your answer in degrees to 1 d.p.
Answers
The value of the angle θ is approximately 24.2 degrees to 1 decimal place.
In a right-angled triangle, the tangent of an angle is defined as the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle. Given that tan θ = 23/52, we can find the value of the angle θ.
To find the value of θ, we can use the inverse tangent or arctan function. Taking the inverse tangent of both sides of the equation, we have:
θ = arctan(23/52)
Using a calculator or trigonometric tables, we can evaluate the inverse tangent of 23/52. The result is approximately 24.2 degrees.
Note that in the context of a right-angled triangle, the tangent function is defined for acute angles (less than 90 degrees). Since 0 degrees is the smallest possible angle, it is considered an acute angle in this case.
For more such questions on angle
https://brainly.com/question/31615777
#SPJ8
Complete the inequality to represent the following: 13 times a number x
is less than or equal to 200.
Answers
The value for the Inequality 13x ≤ 200 is x ≤ 15.384.
What is Inequality?Mathematical expressions with inequalities are those in which the two sides are not equal. Contrary to equations, we compare two values in inequality. Less than (or less than or equal to), greater than (or greater than or equal to), or not equal to signs are used in place of the equal sign.
Given:
13 times a number x is less than or equal to 200.
Now, Writing the Inequality Mathematically
13x ≤ 200
x ≤ 200 / 13
x ≤ 15.384
Learn more about Inequality here:
https://brainly.com/question/2675848
#SPJ1
Two similar solids have a scale factor of 5:3.
What is the ratio of their volumes expressed in lowest terms?
Answers
The ratio of the volumes of the two similar solids that have a scale factor of 5:3 is: 125:27.
How to Determine The Ratio of the Volume of Similar Solids?If two solids that are similar to each other, have volumes A and B respectively, and have a scale factor of a:b, thus, the ratio of their volumes would be expressed as:
Volume of solid A/Volume of solid B = a³/b³
or
Volume of solid A : Volume of solid B = a³ : b³
Thus, the given similar solids have a scale factor of 5:3, therefore, the ratio of their volumes would be expressed as shown below:
5³ : 3³
125 : 27
Thus, the ratio of the volumes of the two similar solids that have a scale factor of 5:3 is: 125:27.
Learn more about the volume of similar solids on:
https://brainly.com/question/16599646
#SPJ1
7(C - 18)= -98
Help ASAP
Answers
Answer:
\(C=4\)
Step-by-step explanation:
\(7(c-18)=-98\\7c \frac{-126}{+126}=\frac{-98}{+126} \\\frac{7c}{7}=\frac{28}{7}\\c=4\)
The base area of a right circular cone is 1/4 of its total surface area. What is the ratio of the radius
to the slant height?
Answers
Given:
The base area of a right circular cone is \(\dfrac{1}{4}\) of its total surface area.
To find:
The ratio of the radius to the slant height.
Solution:
We know that,
Area of base of a right circular cone = \(\pi r^2\)
Total surface area of a right circular cone = \(\pi rl+\pi r^2\)
where, r is radius and l is slant height.
According to the question,
\(\pi r^2=\dfrac{1}{4}(\pi rl+\pi r^2)\)
Multiply both sides by.
\(4\pi r^2=\pi rl+\pi r^2\)
\(4\pi r^2-\pi r^2=\pi rl\)
\(3\pi r^2=\pi rl\)
Cancel out the common factors from both sides.
\(3r=l\)
Now, ratio of the radius to the slant height is
\(\dfrac{r}{l}=\dfrac{r}{3r}\)
\(\dfrac{r}{l}=\dfrac{1}{3}\)
Therefore, the ratio of the radius to the slant height is 1:3.
What is the pre-image of vertex A' if the image shown
on the graph was created by a reflection across the line
y=x?
O (10,-2)
O (-10, 2)
O (-2,-10)
O (2, 10)
Answers
Answer:
it is b
Step-by-step explanation:
The solution is Option A.
The coordinates of the vertex A before the reflection across the line y = x is given by A = A ( 10 , -2 )
What is Reflection?Reflection is a type of transformation that flips a shape along a line of reflection, also known as a mirror line, such that each point is at the same distance from the mirror line as its mirrored point. The line of reflection is the line that a figure is reflected over. If a point is on the line of reflection then the image is the same as the pre-image. Images are always congruent to pre-images.
The reflection of point (x, y) across the x-axis is (x, -y). When you reflect a point across the y-axis, the y-coordinate remains the same, but the x-coordinate is taken to be the additive inverse. The reflection of point (x, y) across the y-axis is (-x, y).
Given data ,
Let the coordinates of the point A be A ( x , y )
Now , the vertex A is reflected over the line y = x
When you reflect a point across the y = x , the y-coordinate gets interchanged with x-coordinate. The reflection of point (x, y) across the line y = xis ( y , x )
So , the coordinates of the point A' ( -2 , 10 )
Now , the coordinates of the point A will be
A ( x , y ) = A ( 10 , -2 )
Therefore , the value of A is A ( 10 , -2 )
Hence , the coordinates of the point before reflection is A ( 10 , -2 )
To learn more about reflection click :
https://brainly.com/question/4681298
#SPJ2
I'll Give brainliest to whoever answers is correct
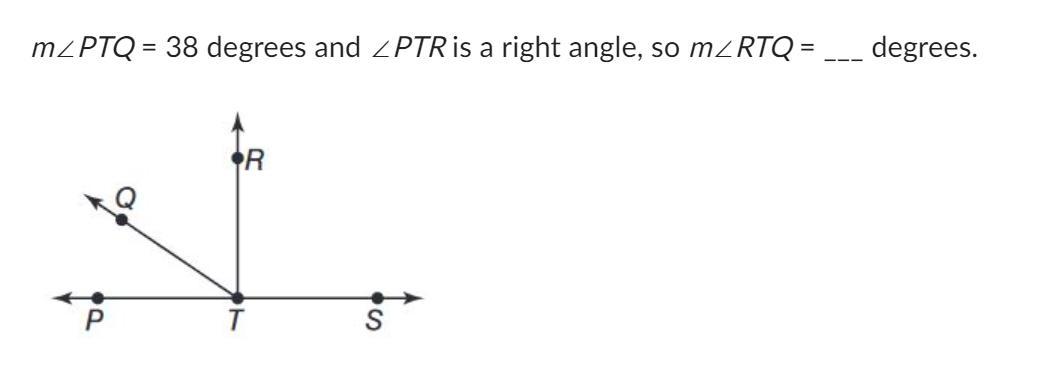
Answers
Answer:
52
Step-by-step explanation:
RTQ is 52 because if PTR is a right angle, right angles equal 90 degrees. So if PTQ is 38 degrees, we subtract 38 from 90 to get RTQ. 90-38 equals 52.
Answer:
52 degrees
Step-by-step explanation:
right angle = 90
90-38=52
So RTQ = 52 degrees
How to find derivative of x^5(1- (5/x+8))
Answers
Answer:
\(5x^4-\frac{25x^4}{x+8}+\frac{5x^5}{(x+8)^2}\)
Step-by-step explanation:
\(f(x)=x^5\\f'(x)=5x^4\\g(x)=1-\frac{5}{x+8}\\g'(x)=\frac{5}{(x+8)^2}\\\\\frac{d}{dx}f(x)g(x)\\\\=f'(x)g(x)+f(x)g'(x)\\\\=5x^4(1-\frac{5}{x+8})+x^5(\frac{5}{(x+8)^2})\\\\=5x^4-\frac{25x^4}{x+8}+\frac{5x^5}{(x+8)^2}\)
Identify the algebraic rule that would translate a figure 3 units left and 2 units up.

Answers
The algebraic rule for translating the figure 3 units left and 2 units up is (x-3, y+2). Option B.
To translate a figure 3 units to the left and 2 units up, we need to adjust the coordinates of the figure accordingly. The algebraic rule that represents this translation can be determined by examining the changes in the x and y coordinates.
When we move a figure to the left, we subtract a certain value from the x coordinates. In this case, we want to move the figure 3 units to the left, so we subtract 3 from the x coordinates.
Similarly, when we move a figure up, we add a certain value to the y coordinates. In this case, we want to move the figure 2 units up, so we add 2 to the y coordinates.
Taking these changes into account, we can conclude that the algebraic rule for translating the figure 3 units left and 2 units up is (x-3, y+2). The x coordinates are shifted by subtracting 3, and the y coordinates are shifted by adding 2. SO Option B is correct.
For more question on algebraic visit:
https://brainly.com/question/30652385
#SPJ8
Evaluate the expression (7+6i)−(−9−8i) and write the result in the form a+bi.
Answers
Remove the parentheses and combine the like terms:
7 - -9 = 7+ 9 = 16
6i - -8i = 6i +8i = 14i
The answer is 16 + 14i
Find the volume of each composite figure to the nearest whole number.

Answers
The volume of the composite figure in this problem is given as follows:
76 ft³.
How to obtain the volume of a rectangular prism?The volume of a rectangular prism, with dimensions defined as length, width and height, is given by the multiplication of these three defined dimensions, according to the equation presented as follows:
Volume = length x width x height.
The figure in this problem is composed by two prisms, with dimensions given as follows:
2 ft, 6 ft and 3 ft.2 ft, 4 ft and 8 - 3 = 5 ft.Hence the volume is given as follows:
2 x 6 x 3 + 2 x 4 x 5 = 76 ft³.
A similar problem about the volume of rectangular prisms is presented at brainly.com/question/22070273
#SPJ1
If a storage tank is holding 450 litres when it is three quarters full, how much will it contain when it is two thirds?
Answers
Answer:
400 litres
Step-by-step explanation:
The function f(x) is graphed below. How many points on the graph represent a relative minimum?

Answers
The only relative minimum found here is at point F because F is the lowest valley point, we have a relative minimum here.
Explain about the function?An expression, rule, or law in mathematics that specifies the relationship between an independent variable and a dependent variable (the dependent variable).
F(x) = x2 is an illustration of a basic function. The function f(x) in this function first squares the value of "x". As an illustration, f(3) = 9 if x = 3. There are other other functions that can be used, such as f(x) = sin x, f(x) = x2 + 3, f(x) = 1/x, f(x) = 2x + 3, etc.
A graph is considered to be a function if any vertical line formed can cross it at most one point. The graph is not a function if it contains any locations where a vertical line can pass through it twice or more.
To learn more about function refer to:
https://brainly.com/question/11624077
#SPJ4
The lifetime for a certain brand of widgets is normally distributed. A random sample of 25 widgets is taken and a sample mean lifetime of 520 hours with a standard deviation of 50 hours. Before taking the sample, researchers claimed that the mean lifetime of a widget was more than 500 hours. 1. null hypothesis:
2. the alternative hypothesis:
3. explain what test will be used and why?
Answers
Answer:
1. H0: u = 500
2. H1: u <500
3. One sample t test
Step-by-step explanation:
1. The null hypothesis in this question would be
H0: u = 500
2. The alternative hypothesis would be
H1: u < 500
3. The test that we are going to be using is the one sample t test. This test is used to test hypothesis. It would make a comparison of h0 to the mean of the sample. Now we are using this here because the sample standard deviation was given
Edouard Manet's Luncheon on the Grass was shown in the ___ after it was rejected for the annual salon.
A. World's Fair
B. Impressionist exhibition
C. salon d'automne
D. Osalon des refuses
Answers
Edouard Manet's Luncheon on the Grass was shown in the Salon des Refuses after it was rejected for the annual salon.
Option D is the correct answer.
We have,
Edouard Manet's painting "Luncheon on the Grass" was first rejected by the Paris Salon in 1863, as it was considered scandalous due to the nudity of the female figure in the painting.
In response to this rejection,
Emperor Napoleon III ordered an exhibition to be held for all the rejected paintings, which was known as the Salon des Refusés (Salon of the Refused).
Thus,
Edouard Manet's Luncheon on the Grass was shown in the Salon des Refuses after it was rejected for the annual salon.
Learn more about Edouard Manet's painting here:
https://brainly.com/question/26188885
#SPJ1
I’m doing my geometry homework and don’t remember the formula or way to solve the lengths of a triangle side with graph points. How do I solve both parts of #1?

Answers
\(~\hfill \stackrel{\textit{\large distance between 2 points}}{d = \sqrt{( x_2- x_1)^2 + ( y_2- y_1)^2}}~\hfill~ \\\\[-0.35em] ~\dotfill\\\\ E(\stackrel{x_1}{2}~,~\stackrel{y_1}{3})\qquad F(\stackrel{x_2}{3}~,~\stackrel{y_2}{1}) ~\hfill EF=\sqrt{(~~ 3- 2~~)^2 + (~~ 1- 3~~)^2} \\\\\\ ~\hfill EF=\sqrt{( 1)^2 + ( -2)^2} \implies \boxed{EF=\sqrt{ 5 }}\)
\(F(\stackrel{x_1}{3}~,~\stackrel{y_1}{1})\qquad D(\stackrel{x_2}{-1}~,~\stackrel{y_2}{-1}) ~\hfill FD=\sqrt{(~~ -1- 3~~)^2 + (~~ -1- 1~~)^2} \\\\\\ ~\hfill FD=\sqrt{( -4)^2 + ( -2)^2} \implies \boxed{FD=\sqrt{ 20 }} \\\\\\ D(\stackrel{x_1}{-1}~,~\stackrel{y_1}{-1})\qquad E(\stackrel{x_2}{2}~,~\stackrel{y_2}{3}) ~\hfill DE=\sqrt{(~~ 2- (-1)~~)^2 + (~~ 3- (-1)~~)^2} \\\\\\ ~\hfill DE=\sqrt{( 3)^2 + (4)^2} \implies DE=\sqrt{ 25 }\implies \boxed{DE=5} \\\\[-0.35em] \rule{34em}{0.25pt}\)
\(E(\stackrel{x_1}{2}~,~\stackrel{y_1}{3})\qquad F(\stackrel{x_2}{3}~,~\stackrel{y_2}{1}) ~\hfill \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{1}-\stackrel{y1}{3}}}{\underset{run} {\underset{x_2}{3}-\underset{x_1}{2}}} \implies \cfrac{ -2 }{ 1 } \implies - 2 \\\\[-0.35em] ~\dotfill\)
\(F(\stackrel{x_1}{3}~,~\stackrel{y_1}{1})\qquad D(\stackrel{x_2}{-1}~,~\stackrel{y_2}{-1}) ~\hfill \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{-1}-\stackrel{y1}{1}}}{\underset{run} {\underset{x_2}{-1}-\underset{x_1}{3}}} \implies \cfrac{ -2 }{ -4 } \implies \cfrac{1 }{ 2 } \\\\[-0.35em] ~\dotfill\)
\(D(\stackrel{x_1}{-1}~,~\stackrel{y_1}{-1})\qquad E(\stackrel{x_2}{2}~,~\stackrel{y_2}{3}) ~\hfill \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{3}-\stackrel{y1}{(-1)}}}{\underset{run} {\underset{x_2}{2}-\underset{x_1}{(-1)}}} \implies \cfrac{3 +1}{2 +1} \implies \cfrac{4 }{ 3 }\)
A toy house has the dimension as shown below. A hobbyist has a bottle of paint that can cover a total of 1000 square centimeters. If the bottle of paint is full when the hobbyist starts painting, what percentage of the bottle is used to cover the entire house except for the bottom of the rectangular prism?

Answers
Calculate the area of each face that is covered by the paint:
Area of 1 and 4:
Use Pythagorean theorem to find 1/2 b:
\(\begin{gathered} \frac{1}{2}b=\sqrt[]{(5\operatorname{cm})^2-(4\operatorname{cm})^2} \\ \\ \frac{1}{2}b=\sqrt[]{25\operatorname{cm}^2+16cm^2} \\ \\ \frac{1}{2}b=\sqrt[]{41cm^2} \\ \\ b=2\sqrt[]{41}cm \\ \\ \\ A_1=A_4=\frac{1}{2}b\cdot h \\ \\ A_1=A_4=\frac{1}{2}(2\sqrt[]{41}cm)(4\operatorname{cm}) \\ \\ A_1=A_4=4\sqrt[]{41}cm^2 \end{gathered}\)Area of 2 and 3:
\(\begin{gathered} A_2=A_3=w\cdot l \\ \\ A_2=A_3=5\operatorname{cm}\cdot9\operatorname{cm} \\ \\ A_2=A_3=45cm^2 \end{gathered}\)Area of 5 and 7:
\(\begin{gathered} A_5=A_7=w\cdot l \\ \\ \\ A_5=A_7=6\operatorname{cm}\cdot7\operatorname{cm} \\ \\ A_5=A_7=42\operatorname{cm} \end{gathered}\)Area of 6 and 8:
\(\begin{gathered} A_6=A_8=w\cdot l \\ \\ A_6=A_8=9\operatorname{cm}\cdot7\operatorname{cm} \\ \\ A_6=A_8=63\operatorname{cm}^2 \end{gathered}\)Then, the total area cover by the paint is:
\(\begin{gathered} A_T=A_1+A_2+A_3+A_4+A_5+A_6+A_7+A_8_{} \\ \\ A_T=(4\sqrt[]{41}+45+45+4\sqrt[]{41}+42+63+42+63)cm^2 \\ \\ A_T=(300+8\sqrt[]{41})cm^2 \\ \\ A_T\approx351.2\operatorname{cm}^2 \end{gathered}\)If the paint can cover 1000 square centimeters the percentage used to cover the entire house is: 35.12%\(351.2\operatorname{cm}\cdot\frac{100}{1000\operatorname{cm}^2}=35.12\)


the sale price of any item in a store is 85 percent off it's usual price what is a 18 dallor sweaters sale price
Answers
The sale price of the sweater is $2.7
How to determine the sales price of the sweater?From the question, we have the following parameters that can be used in our computation:
Markdown rate = 85% off
Original price of the sweater = $18
The retail price of the coat can be calculated using the following equation
Retail price = original price * (1 - Markdown rate)
Substitute the known values in the above equation, so, we have the following representation
Retail price = 18 * (1 - 85%)
Evaluate the products
Retail price = 2.7
Hence, the sales price is $2.7
Read more about markup at
brainly.com/question/19104371
#SPJ1
write your answer as an integer or as a decimal rounded to the nearest tenth

Answers
Answer:
Step-by-step explanation:
CE and are the sides making up the sine of an angle.
CE is the side opposite the angle
DE is the side hypotenuse.
<D = 61 degrees
Sin(D) = opposite / hypotenuse
hypotenuse = 8
Sin(61) = 0.8746
CE = ?
sin(61) = CE / 8 multiply both sides by 8
8 sin(61) = CE
CE = 8 * 0.8746
CE = 6.9969
CE = 7.0
That 0 should be included in the answer, but I think it is safe to say that if you enter 7, you will get it right.
Answer:
7.0
Step-by-step explanation:

Simplify (2a^3a^4)^5. Show all work
Answers
Answer:
(2a^3a^4)^5 simplifies to 32a^35.
Step-by-step explanation:
To simplify (2a^3a^4)^5, we can use the properties of exponents which states that when we raise a power to another power, we can multiply the exponents. Therefore, we can rewrite the expression as:
(2a^3a^4)^5 = 2^5 * (a^3a^4)^5
Next, we can simplify the expression inside the parentheses by multiplying the exponents:
a^3a^4 = a^(3+4) = a^7
Substituting this into our expression, we get:
(2a^3a^4)^5 = 2^5 * (a^3a^4)^5 = 2^5 * a^35
Finally, we can simplify this expression by using the property of exponents that states that when we multiply two powers with the same base, we can add their exponents. Therefore, we can rewrite the expression as:
2^5 * a^35 = 32a^35
Therefore, (2a^3a^4)^5 simplifies to 32a^35.
write the point slope form of an equation with a slope of eight and a Y intercept of five
Answers
Answer:
y=8x+5
Step-by-step explanation:
pleasr help me out with this

Answers
Answer:
3π - π√2/2 or 7.2 cm-------------------------
According to the given we can state:
AD = BC = AB = 2AO = 2,EO is the perpendicular bisector of AB,Arc AC and arc BD are of equal length.Find arc AB, it is a semicircle of 1 cm radius:
arc(AB) = 1/2 × 2πr = πr = π cmΔAEO and ΔBEO are both isosceles, hence ∠A and ∠B are both 45°.
Find arcs ABD and BAC:
arc(ABD) + arc(BAC) = 2 × 45/360 × 2πr = 1/2 × πr = π cm∠AEB is a right angle since ∠AEO and ∠BEO are both 45°.
Hence ∠CED is also right angle as vertical angle with ∠AEB.
Find the length of EC and ED.
We know AD = BC = 2 cm and ΔAEO is 45° right triangle.
It gives us:
AE = √2Then:
ED = AD - AE = 2 - √2Find arc ECD:
arc(ECD) = 1/4 × 2πr = 1/2 × π(2 - √2) = π - π√2/2 cmThe perimeter is the sum of all the arc measures:
P = π + π + π - π√2/2 = 3π - π√2/2 or 7.2 cm (rounded)Answer:
\(\textsf{Perimeter}=3\pi-\dfrac{\pi}{\sqrt{2}}=7.20333649...\; \sf cm\)
Step-by-step explanation:
\(\boxed{\begin{minipage}{6.4 cm}\underline{Arc length}\\\\Arc length $=r \theta$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius. \\ \phantom{ww}$\bullet$ $\theta$ is the angle measured in radians.\\\end{minipage}}\)
To convert degrees to radians, multiply the angle in degrees by π/180°.
Arc AB
As arc AB has center O, the radius of arc AB is OA = 1 cm.
As AB is a straight line, ∠AOB is 180° = π.
Therefore, the length of arc AB is:
\(\implies AB=r \:\theta=1 \cdot \pi = \pi\)
Arc AC
Triangle BOE is a right triangle with base of 1 cm and height of 1 cm.
Therefore, ∠OBE is 45° = π/4
If arc AC has center B, then the radius is AB = 2 cm.
Therefore, the length of arc AC is:
\(\implies AC=r \:\theta=2 \cdot \dfrac{\pi}{4} = \dfrac{\pi}{2}\)
Arc BD
Arc BD is the same as arc AC.
\(\implies BC= \dfrac{\pi}{2}\)
Arc CD
As triangle BOE is a right triangle with base of 1 cm and height of 1 cm, the length of its hypotenuse BE is:
\(\implies BE=\sqrt{1^2+1^2}=\sqrt{2}\)
As arc AC has center B and radius of AB = 2 cm, then BC is also its radius and therefore BC = 2 cm
Therefore:
\(\implies CE=BC-BE\)
\(\implies CE=2-\sqrt{2}\)
The arc CD has center E so its radius is CE = 2-√2.
As ∠BEO and ∠AEO are both 45° then ∠AEB is 90°.
According to the vertical angle theorem, ∠CED is also 90° = π/2.
Therefore, the length of arc CD is:
\(\implies CD=r \:\theta=(2-\sqrt{2}) \cdot \dfrac{\pi}{2} = \dfrac{(2-\sqrt{2})\pi}{2}\)
Perimeter of the egg
The perimeter of the egg is the sum of the found arcs:
\(\implies \textsf{Perimeter}=AB+AC+BD+CD\)
\(\implies \textsf{Perimeter}=\pi+\dfrac{\pi}{2}+\dfrac{\pi}{2}+\dfrac{(2-\sqrt{2})\pi}{2}\)
\(\implies \textsf{Perimeter}=2\pi+\dfrac{(2-\sqrt{2})\pi}{2}\)
\(\implies \textsf{Perimeter}=2\pi+\dfrac{2 \pi}{2}-\dfrac{\sqrt{2}\:\pi}{2}\)
\(\implies \textsf{Perimeter}=3\pi-\dfrac{\sqrt{2}\:\pi}{2}\)
\(\implies \textsf{Perimeter}=3\pi-\dfrac{\pi}{\sqrt{2}}\)
\(\implies \textsf{Perimeter}=7.20333649...\; \sf cm\)
