Answers
Related Questions
A piece of fabric is 4 1/6 yards long. If 2 1/4 yards are cut off, how many yards remain?
Answers
hope this helps ;)
Given the lengths of the sides of a triangle, determine if it is an acute, anobtuse, or a right triangle.

Answers
Use the Pythagorean theorem to determine if the triangle is acute, obtuse or right triangle.
\(\begin{gathered} a^2+b^2=c^2 \\ \text{where} \\ c\text{ is the longest side of the triangle} \\ a\text{ and }b\text{ are the other 2 sides} \end{gathered}\)\(\begin{gathered} a^2+b^2=c^2 \\ (18)^2+(29)^2\questeq(46)^2 \\ 324+841\questeq2116 \\ 1165\questeq2116 \\ 1165<2116 \end{gathered}\)\(\begin{gathered} \text{IF} \\ a^2+b^2c^2 \\ \text{THEN, the triangle is an acute triangle} \\ \\ \text{IF} \\ a^2+b^2=c^2 \\ \text{THEN, the triangle is a right triangle} \end{gathered}\)Since the sum of the square of the side of the two angles is less than the square of the longest side, then given the length of a triangle 18-29-46, the triangle is an obtuse triangle.
how to calculate the weight of a floor with 150 pcf
Answers
To calculate the weight of a floor with 150 pcf (pounds per cubic foot), you need to know the volume of the floor in cubic feet. Once you know the volume, you can multiply it by 150 to get the weight in pounds.
For example, if the floor has a length of 20 feet, a width of 10 feet, and a thickness of 0.5 feet, the volume would be:
Volume = Length x Width x Thickness
Volume = 20 x 10 x 0.5
Volume = 100 cubic feet
To calculate the weight of the floor with 150 pcf, you would multiply the volume by 150:
Weight = Volume x Pcf
Weight = 100 x 150
Weight = 15,000 pounds
So the weight of the floor would be 15,000 pounds.
Learn more about weight at https://brainly.com/question/14571202
#SPJ11
The weight of this floor would be 6,000 pounds.
To calculate the weight of a floor with a density of 150 pounds per cubic foot (pcf),
you need to know the volume of the floor.
Let's assume that the floor has a rectangular shape, with a length of L feet, a width of W feet, and a thickness of T feet. The volume of the floor can be calculated as:
V = L × W × T
Once you have the volume, you can calculate the weight using the formula:
Weight = Density × Volume
In this case, the density is 150 pcf. Substituting the value of V, we get:
Weight = 150 × L × W × T
So if, for example, the floor has a length of 10 feet, a width of 8 feet, and a thickness of 0.5 feet (i.e., 6 inches), then the volume would be:
V = 10 × 8 × 0.5 = 40 cubic feet
And the weight would be:
Weight = 150 × 10 × 8 × 0.5 = 6,000 pounds
Therefore, the weight of this floor would be 6,000 pounds.
Click the below link, to learn more about Weight:
https://brainly.com/question/31166130
#SPJ11
A truck has a mass of 5000 kg. The truck driver presses on the brakes. The unbalanced net force acting on the truck when the brakes were applied was 6000N. What is the truck’s Acceleration?
Answers
The acceleration of the truck when it has a mass of 5000 kg and the truck driver presses on the brakes is 1.2m/s².
What is acceleration?The rate of change of an object's velocity with respect to time is defined as acceleration. Vector quantities are accelerations.
The orientation of an object's acceleration is determined by the orientation of the net force acting on that object's acceleration, which is the rate at which velocity changes over time in terms of both speed and direction. A point or object moving in a straight line is accelerated if it accelerates or decelerates.
Acceleration will be:
= Force / mass
= 6000 / 5000
= 1.2 m/s²
Learn more about acceleration on:
https://brainly.com/question/460763
#SPJ1
herry uses the steps below to solve the equation x + (negative 8) = 3 x + 6.
Step 1 Add 1 negative x-tile to both sides and create zero pairs
Step 2 Add 8 positive unit tiles to both sides and create zero pairs.
Step 3 Divide the 14 unit tiles evenly among the 2 x-tiles.
Step 4 The solution is x = 7
What is Sherry’s error?
In step 1, she should have added 3 negative x-tiles to both sides.
In step 2, she should have added 6 negative unit tiles to both sides.
In step 3, she did not divide the tiles evenly.
In step 4, she should have found the solution x = negative 1.
Answers
Add 8 positive unit tiles to both sides and create zero pairs.
What is the equation?
The definition of an equation in algebra is a mathematical statement that demonstrates the equality of two mathematical expressions.
Here, we have
Given:
Herry uses the steps below to solve the equation x + (negative 8) = 3 x + 6.
x + (- 8) = 3 x + 6
x- 8 = 3x +6
First,
Add 8 positive unit tiles to both sides
x- 8 + 8 = 3x +6 + 8
x= 3x +14
This creates pair
3x-x = -14
x= -7
Hence, add 8 positive unit tiles to both sides and create zero pairs.
To learn more about the equation from the given link
https://brainly.com/question/25976025
#SPJ1
Which expression is equivalent to 4(2.61y − 3.08)
Answers
Answer:
10.44y - 12.32
Step-by-step explanation:
Use the distributive property.
4(2.61y − 3.08) =
= 10.44y - 12.32
GUYYS I NEED HELPP ASAP!!!!
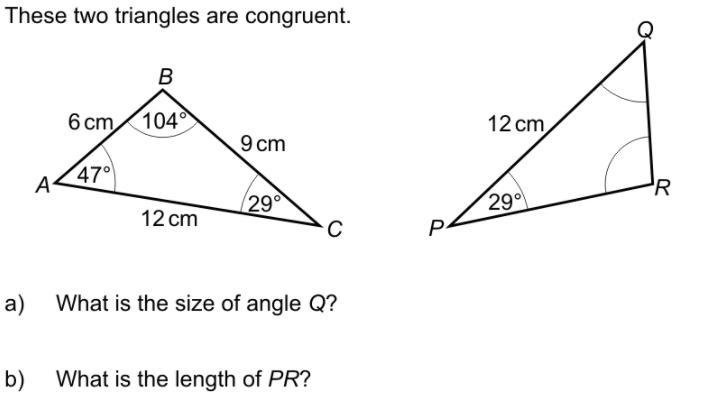
Answers
Answer:
Q: 47°
length of PR: 9cm
I'm pretty sure that's the answer
Find the distance traveled by a particle with position (x, y) as t varies in the given time interval.
x = 4 sin^2(t), y = 4 cos^2(t), 0 ≤ t ≤ 5π
What is the length of the curve?
Answers
Hence, the length of the curve defined by the parametric equations x = 4sin^2(t) and y = 4cos^2(t) over the interval 0 ≤ t ≤ 5π is 20π units.
To find the distance traveled by the particle, we need to calculate the length of the curve defined by the parametric equations x = 4sin^2(t) and y = 4cos^2(t) over the given time interval 0 ≤ t ≤ 5π.
We can use the arc length formula to calculate the length of the curve. The arc length formula for a parametric curve defined by x = f(t) and y = g(t) is given by:
L = ∫[a, b] √[f'(t)^2 + g'(t)^2] dt
where f'(t) and g'(t) are the derivatives of f(t) and g(t) with respect to t.
Let's start by finding the derivatives of x and y with respect to t:
x = 4sin^2(t)
x' = d/dt(4sin^2(t))
= 8sin(t)cos(t)
= 4sin(2t)
y = 4cos^2(t)
y' = d/dt(4cos^2(t))
= -8cos(t)sin(t)
= -4sin(2t)
Now, let's calculate the length of the curve using the arc length formula:
L = ∫[0, 5π] √[x'(t)^2 + y'(t)^2] dt
= ∫[0, 5π] √[16sin^2(2t) + 16sin^2(2t)] dt
= ∫[0, 5π] √[32sin^2(2t)] dt
= ∫[0, 5π] √[32sin^2(2t)] dt
= ∫[0, 5π] 4√[2sin^2(2t)] dt
= 4∫[0, 5π] √[2sin^2(2t)] dt
= 4∫[0, 5π] √[2(1 - cos^2(2t))] dt
= 4∫[0, 5π] √[2(1 - (1 - 2sin^2(t))^2)] dt
= 4∫[0, 5π] √[2(2sin^4(t))] dt
= 4∫[0, 5π] √[8sin^4(t)] dt
= 4∫[0, 5π] 2sin^2(t) dt
= 8∫[0, 5π] sin^2(t) dt
We can use the trigonometric identity sin^2(t) = (1 - cos(2t))/2 to simplify the integral further:
L = 8∫[0, 5π] sin^2(t) dt
= 8∫[0, 5π] (1 - cos(2t))/2 dt
= 4∫[0, 5π] (1 - cos(2t)) dt
= 4∫[0, 5π] dt - 4∫[0, 5π] cos(2t) dt
The integral of dt over the interval [0, 5π] is simply the length of the interval, which is 5π - 0 = 5π. The integral of cos(2t) over the same interval is zero since the cosine function is periodic with period π.
Therefore, the length of the curve is given by:
L = 4(5π) - 4(0)
= 20π
To know more about parametric equations,
https://brainly.com/question/31399244
#SPJ11
The volume of a cylinder is 448 pi cm³ and the height is 7 cm.Find its radius.
Answers
The formula for the volume of a cylinder is given by:
\(V=\pi r^2h\)Where r is the base radius and h is the height.
If the volume is 448*pi cm³ and the height is 7 cm, we have:
\(\begin{gathered} 448\pi=\pi r^2\cdot7\\ \\ 448=7r^2\\ \\ r^2=\frac{448}{7}\\ \\ r^2=64\\ \\ r=8\text{ cm} \end{gathered}\)Therefore the radius is equal to 8 cm.
Drawing this cylinder, we have:
help 4. Analysis and Making Production Decisions a) On Monday, you have a single request: Order A for 15,000 units. It must be fulfilled by a single factory. To which factory do you send the order? Explain your decision. Support your argument with numbers. b) On Tuesday, you have two orders. You may send each order to a separate factory OR both to the same factory. If they are both sent to be fulfilled by a single factory, you must use the total of the two orders to find that factory’s cost per unit for production on this day. Remember that the goal is to end the day with the lowest cost per unit to produce the company’s products. Order B is 7,000 units, and Order C is 30,000 units. c) Compare the two options. Decide how you will send the orders out, and document your decision by completing the daily production report below.


Answers
A) we would send Order A to Factory 3.
B) we would send both Order B and Order C to Factory 3.
B 7,000 Factory 3
C 30,000 Factory 3
Total number of units produced for the company today: 37,000
Average cost per unit for all production today: $9.00
To make decisions about which factory to send the orders to on Monday and Tuesday, we need to compare the costs per unit for each factory and consider the total number of units to be produced. Let's go through each day's scenario and make the production decisions.
a) Monday: Order A for 15,000 units
To decide which factory to send the order to, we compare the costs per unit for each factory. We select the factory with the lowest cost per unit to minimize the average cost per unit for the company.
Let's assume the costs per unit for each factory are as follows:
Factory 1: $10 per unit
Factory 2: $12 per unit
Factory 3: $9 per unit
To calculate the total cost for each factory, we multiply the cost per unit by the number of units:
Factory 1: $10 * 15,000 = $150,000
Factory 2: $12 * 15,000 = $180,000
Factory 3: $9 * 15,000 = $135,000
Based on the calculations, Factory 3 has the lowest total cost for producing 15,000 units, with a total cost of $135,000. Therefore, we would send Order A to Factory 3.
b) Tuesday: Order B for 7,000 units and Order C for 30,000 units
We have two options: sending each order to a separate factory or sending both orders to the same factory. We need to compare the average cost per unit for each option and select the one that results in the lowest average cost per unit.
Let's assume the costs per unit for each factory remain the same as in the previous example. We will calculate the average cost per unit for each option:
Option 1: Sending orders to separate factories
For Order B (7,000 units):
Average cost per unit = ($10 * 7,000) / 7,000 = $10
For Order C (30,000 units):
Average cost per unit = ($9 * 30,000) / 30,000 = $9
Total number of units produced for the company today = 7,000 + 30,000 = 37,000
Average cost per unit for all production today = ($10 * 7,000 + $9 * 30,000) / 37,000 = $9.43 (rounded to two decimal places)
Option 2: Sending both orders to the same factory (Factory 3)
For Orders B and C (37,000 units):
Average cost per unit = ($9 * 37,000) / 37,000 = $9
Comparing the two options, we see that both options have the same average cost per unit of $9. However, sending both orders to Factory 3 simplifies the production process by consolidating the orders in one factory. Therefore, we would send both Order B and Order C to Factory 3.
Production Report for Tuesday:
Order # of Units Factory
B 7,000 Factory 3
C 30,000 Factory 3
Total number of units produced for the company today: 37,000
Average cost per unit for all production today: $9.00
for more such question on production visit
https://brainly.com/question/31135471
#SPJ8
Consider a general linear programming problem and suppose that we have a nondegenerate basic feasible solution to the primal. Show that the complementary slackness conditions lead to a system of equations for the dual vector that has a unique solution.
Answers
Linear programming problems are mathematical optimization problems where a linear objective function is subject to linear constraints. These problems can be solved using a variety of methods, including the simplex method and interior point methods.
A nondegenerate basic feasible solution is a solution to a linear programming problem where all the constraints are satisfied and the number of non-zero variables is equal to the number of constraints. This means that the solution is not at the corner of the feasible region and there is no redundant constraint.
Complementary slackness conditions are a set of conditions that must be satisfied by any optimal solution to a linear programming problem. These conditions state that the product of the slack variables (the difference between the left-hand side and right-hand side of a constraint) and the corresponding dual variable must be equal to zero.
Suppose we have a nondegenerate basic feasible solution to the primal. Then, the complementary slackness conditions will lead to a system of equations for the dual vector. Since the solution is nondegenerate, this system of equations will have a unique solution. This is because there are no redundant constraints, so the number of equations will be equal to the number of variables. Additionally, the complementary slackness conditions ensure that the system is not underdetermined or overdetermined.
Therefore, if we have a nondegenerate basic feasible solution to the primal, the complementary slackness conditions will lead to a system of equations for the dual vector that has a unique solution. This is an important result in linear programming, as it helps us to understand the relationship between primal and dual problems and the existence and uniqueness of solutions.
Learn more about Linear programming here:
https://brainly.com/question/31758568
#SPJ11
PLEASE HELP ME GET THIS .

Answers
Answer:
2
Step-by-step explanation:
because the 8 feet used on a ladder on level at the ground from the side of a house.
cr2o72−(aq) 14h (aq) 6i−(aq)→2cr3 (aq) 7h2o(l) 3i2(s)cr2o72−(aq) 14h (aq) 6i−(aq)→2cr3 (aq) 7h2o(l) 3i2(s) express your answer in volts using two decimal places.
Answers
The cell potential (E⁰ cell) of the given reaction Cr₂O₇²⁻ (aq) + 14H⁺ (aq) + 6I⁻ (aq) → 2Cr³⁺ (aq) + 7H₂O (l) + 3I₂ (s) is 0.79 volts.
The given reaction is a redox reaction involving the following species: Cr₂O₇²⁻ (aq) + 14H⁺ (aq) + 6I⁻ (aq) → 2Cr³⁺ (aq) + 7H₂O (l) + 3I₂ (s) .
To determine the cell potential (E⁰) of the reaction, we need to know the reduction potentials (E⁰) of the species involved. The reduction half-reactions involved in this reaction are:
Cr₂O₇²⁻ (aq) + 14H⁺ (aq) + 6e⁻→ 2Cr³⁺ (aq) + 7H₂O (l)
(1) I2 (s) + 2e⁻ → 2I⁻ (aq)
(2) The standard reduction potentials (E⁰) for these half-reactions are: E⁰(Cr₂O₇²⁻/Cr³⁺) = 1.33 V
E⁰(I2/I⁻) = 0.54 V
To calculate the cell potential (E⁰cell), we subtract the reduction potential of the anode reaction (oxidation half-reaction) from the reduction potential of the cathode reaction (reduction half-reaction):
E⁰cell = E⁰cathode - E⁰anode
In this case, the reduction half-reaction (1) involves Cr₂O₇²⁻/Cr³⁺ and has a higher reduction potential (1.33 V) compared to the reduction half-reaction (2) involving I2/I⁻ (0.54 V).
Therefore, the reduction half-reaction (1) is the cathode reaction, and the reduction half-reaction (2) is the anode reaction. Substituting the values into the equation, we get:
E⁰cell = 1.33 V - 0.54 V = 0.79 V
Therefore, the cell potential (E⁰cell) of the given reaction is 0.79 volts.
To learn more about cell potential: https://brainly.com/question/1313684
#SPJ11
Your employer offers a 401(k) plan in which they will match 100% of
your contributions, up to 5% of your salary. Suppose you make
$35,000 in a given year, and you contribute $4,000.
Answers
Answer:
they will match 5% of 35,000 = $1750
so you total would be $5,750
Step-by-step explanation:
In the figure below, Z is the center of the circle. Suppose that OR=4, ST= 4, UZ= 6, and VZ=4x-6. Find the following.

Answers
Answer:
x = 3 units
SV = 2 units
Step-by-step explanation:
In\( \odot Z\) QR and ST are chords such that:
QR = ST = 4
That is both the chords are equal in measure.
Equal chords are at equal distance from the center of the circle. Therefore,
VZ = UZ
4x - 6 = 6
4x = 6 + 6
4x = 12
x = 12/4
x = 3 units
Since, perpendicular dropped from the center of the circle bisects the chord.
\( \therefore SV = \frac{1}{2} ST\)
\( \therefore SV = \frac{1}{2} \times 4\)
\( \therefore SV = 2\: units\)
let f (x) = x3 ln(1 x2), and let [infinity] Σ anx^n n=0be the taylor series of f about 0. thena3=a7=a12=
Answers
a₃ = a₇ = a₁₂ = 0. To find the values of a3, a7, and a12 in the Taylor series of f(x) = x^3 ln(1 - x^2) about 0, we need to determine the coefficients of the corresponding terms in the series expansion.
The general formula for the coefficients in the Taylor series expansion of a function f(x) about 0 is given by:
an = f⁽ⁿ⁾(0) / n!
where f⁽ⁿ⁾(0) represents the nth derivative of f evaluated at 0.
Let's calculate the derivatives of f(x) and evaluate them at 0 to find the coefficients.
f(x) = x^3 ln(1 - x^2)
f'(x) = 3x^2 ln(1 - x^2) + x^3 * (1 - x^2)^(-1)
f''(x) = 6x ln(1 - x^2) + 3x^2 * (1 - x^2)^(-1) - 6x^4 * (1 - x^2)^(-2)
f⁽³⁾(x) = 6 ln(1 - x^2) + 6x * (1 - x^2)^(-1) - 12x^3 * (1 - x^2)^(-2) + 24x^5 * (1 - x^2)^(-3)
Now, let's evaluate these derivatives at 0:
f(0) = 0
f'(0) = 0
f''(0) = 6
f⁽³⁾(0) = 6
The coefficients of the terms in the Taylor series expansion are determined by these derivatives. Specifically, the nth coefficient aₙ is equal to f⁽ⁿ⁾(0) / n!.
Therefore, we have:
a₃ = f⁽³⁾(0) / 3! = 6 / 6 = 1
a₇ = f⁽⁷⁾(0) / 7! = 0 / 5040 = 0
a₁₂ = f⁽¹²⁾(0) / 12! = 0 / 479,001,600 = 0
Hence, a₃ = a₇ = a₁₂ = 0.
Learn more about Taylor series here:
https://brainly.com/question/32235538
#SPJ11
Homes bulit in the suburbs typically have none to three-car garages. Let X be the number of garage stalls per hime found in a sample of 200 homes in a local suburban area. From the data obtained,P(X=0) =0.06, P(X=1) = 0.45 and P(X=2) = 0.32. Find the mean number of garage stalls per home for the sample of home.
a. 1.09
b. 1.15
c. 1.5
d. 1.6
e. 2
Answers
The mean number of garage stalls per home in the sample of 200 homes is 1.09.
What is mean?The mean is a measure of central tendency in statistics that represents the average value of a set of numerical data. It is calculated by summing up all the values and dividing by the total number of values.
According to the given information:
To find the mean number of garage stalls per home in the sample of 200 homes, we need to calculate the expected value or the average value of X, which is the number of garage stalls per home. We are given the probabilities of X taking the values 0, 1, and 2, which are P(X=0) = 0.06, P(X=1) = 0.45, and P(X=2) = 0.32.
The formula for calculating the expected value of X is:
E(X) = Σ [ x × P(X=x) ]
where Σ represents the sum of all values of x, and P(X=x) is the probability of X taking the value x.
Using this formula, we can calculate the expected value of X as follows:
\(E(X) = (0 * 0.06) + (1 * 0.45) + (2 * 0.32)\)
\(= 0 + 0.45 + 0.64\)
= 1.09
Therefore, the mean number of garage stalls per home in the sample of 200 homes is 1.09. Hence, the correct option is (a) 1.09.
To know more about mean visit :
https://brainly.com/question/12019147
#SPJ1
The mean number of garage stalls per home in the sample of 200 homes is 1.09.
What is mean?
The mean is a measure of central tendency in statistics that represents the average value of a set of numerical data. It is calculated by summing up all the values and dividing by the total number of values.
According to the given information:
To find the mean number of garage stalls per home in the sample of 200 homes, we need to calculate the expected value or the average value of X, which is the number of garage stalls per home. We are given the probabilities of X taking the values 0, 1, and 2, which are P(X=0) = 0.06, P(X=1) = 0.45, and P(X=2) = 0.32.
The formula for calculating the expected value of X is:
E(X) = Σ [ x × P(X=x) ]
where Σ represents the sum of all values of x, and P(X=x) is the probability of X taking the value x.
Using this formula, we can calculate the expected value of X as follows:
E(x) = (0.06*0)+(1*0.45)+(2*0.32)
= 1.09
Therefore, the mean number of garage stalls per home in the sample of 200 homes is 1.09. Hence, the correct option is (a) 1.09.
To know more about mean visit :
https://brainly.com/question/12019147
#SPJ1
Factored Form:5r + 4r^4I NEED ALL THE EQUATION PLEASE
Answers
to factor we must recognize the elements in common
the r exist on both terms, so we can divide by r on each term to factor
\(undefined\)which statement best explain the relationship between numbers divisable by 9 and 3
Answers
Answer/Step-by-step explanation:
All numbers that are divisible by 9 are also divisible by 3.
Since 3 goes into 9, if 9 is a factor, 3 is also a factor.
Example:
81 is divisible by 9.
So, 81 is also divisible by 3.
Another example:
1,273,050 is divisible by 9.
So 1,273,050 is also divisible by 3.
But the other way around is not necessarily true. If 3 goes into a number, 9 may or may not go into the number.
That is, if a number is divisible by 3, you cannot necessarily know that it is divisible by 9.
Example (seems like it works):
18 is divisible by 3. 18 is also divisible by 9.
But it doesn't work every single time so it cannot be a rule.
Example(sometimes it doesn't work):
24 is divisible by 3.
24 is not divisible by 9.
A store manager kept track of the number of newspapers sold each week over a seven-week period. The results are shown below. \( 87,87,215,154,288,235,231 \) Find the median number of newspapers sold.
Answers
The median number of newspapers sold over seven weeks is 223.
The median is the middle score for a data set arranged in order of magnitude. The median is less affected by outliers and skewed data.
The formula for the median is as follows:
Find the median number of newspapers sold. (87, 87, 215, 154, 288, 235, 231)
We'll first arrange the data in ascending order.87, 87, 154, 215, 231, 235, 288
The median is the middle term or the average of the middle two terms. The middle two terms are 215 and 231.
Median = (215 + 231)/2
= 446/2
= 223
In statistics, the median measures the central tendency of a set of data. The median of a set of data is the middle score of that set. The value separates the upper 50% from the lower 50%.
Hence, the median number of newspapers sold over seven weeks is 223.
To know more about the median, visit:
brainly.com/question/300591
#SPJ11
How would I solve the problem:Use the equations to solve the system of equations Y=0X=7
Answers
System of Equations
Solve the system
y = 0
x = 7
The solution of this system can be directly expressed as the ordered pair (7,0), but we can also draw the graph for both equations as follows.
The solution of the system is the black dot where both lines intersect, i.e. the point (7,0)

what is z? -0.25z = -1.25
Answers
Answer:
z = 5
Step-by-step explanation:
-0.25z = -1.25
-1.25 ÷ -0.25 = 5
z = 5
pls help me sort these from least to greatest

Answers
Answer:
53/8, 6 17/25, 6.71, 6.713
Step-by-step explanation:
6.713, 6.71, 53/8, 6 17/25
53/8 = 6.625
6 17/25 = 167/25 = 6.68
So, the order from least to greatest is: 53/8, 6 17/25, 6.71, 6.713
9. Sandy bought a laptop for $500.
She had a coupon for 25% off. She
still needs to pay 8% tax. How
much did he pay for the laptop?
Answers
Answer:
final price:400
tax amount:100
25% of 500 is 125$ so then you need to add tax onto that
8% of 125$ is 10 so add 10 to 125 which equals 135$
she paid 135$
Ducklings cost $15 each. Chicks cost $12 each. You have $60 to spend on poultry
Answers
Answer:
If your question is how much money you have after you purchase a duckling and a chick, your answer would be $33. It seems to me like you posted the question without finishing it. I'm guessing you were about to mention how many ducklings and chicks you were going to buy and how much money you would have leftover for the poultry.
Step-by-step explanation:
To solve your problem you must add what you're buying and then subtract from your original amount.
For example: if you want one duckling and one chick and you would like to know how much money you have leftover to buy poultry. $15 + $12= $27 dollars in all. Then, you will subtract $27 dollars from $60, this way you know how much money you will have left in order to buy the poultry. $60 - $27= $33.
Let an = 5n/4n + 1 Determine whether {an) is convergent. convergent divergent
Answers
To determine whether the sequence {an} = 5n/4n + 1 is convergent or divergent, we can analyze its behavior as n approaches infinity.
First, let's rewrite the expression for the nth term of the sequence:
an = 5n / (4n + 1)
As n approaches infinity, the denominator 4n + 1 becomes dominant compared to the numerator 5n. Therefore, we can simplify the expression by neglecting the term 5n:
an ≈ n / (4n + 1)
Now, we can consider the limit of the sequence as n approaches infinity:
lim(n→∞) n / (4n + 1)
To evaluate this limit, we can divide both the numerator and denominator by n:
lim(n→∞) (1 / 4 + 1/n)
As n approaches infinity, the term 1/n approaches zero, leaving us with:
lim(n→∞) 1 / 4 = 1/4
Since the limit of the sequence is a finite value (1/4), we can conclude that the sequence {an} = 5n/4n + 1 is convergent.
In other words, as n gets larger and larger, the terms of the sequence {an} get closer and closer to the limit of 1/4. This indicates that the sequence approaches a fixed value and does not exhibit wild oscillations or diverge to infinity. Therefore, we can say that the sequence is convergent.
To learn more about convergent click here:
brainly.com/question/31756849
#SPJ11
3. Pelton wheel runner produces 20 MW under a head of 450 m when running at a speed of 600 rpm. If the mean runner diameter is 10 times the diameter of jet, determine the number of jets, diameter of eiach jet, diameter of wheel, and discharge. The overall efficiency, coefficient of velocity, and speed ratio are 0.85, 0.98, and 0.47, respectively
Answers
The diameter of each jet is 0.224 m, the diameter of the wheel is 2.24 m, and the number of jets is 150. The discharge through each jet is 1.33 m³/s, and the area of the wheel is 7.24 m².
Given the data for a Pelton wheel, with a power of 20 MW, a head of 450 m, a speed of 600 rpm, an overall efficiency of 0.85, a coefficient of velocity of 0.98, and a speed ratio of 0.47, we can calculate various parameters.
Assuming the number of jets as n, the power delivered by each jet is 20,000/n MW. The discharge through each jet is 200/n m³/s, and the area of each jet is 100π/n d⁴ m².
Learn more about diameter
https://brainly.com/question/1594145
#SPJ11
Let A Є Mnxn (R). Prove or disprove the following statements. (a) If (Ay) (AT) y for all 7,7 R", then A = AT. . = .
(b) If x · (Ax) = (Ax)· x for all x R", then A = AT.
Answers
(a) If (Ay)(AT)y holds for all y in R^n, then A = AT.
(b) The property x · (Ax) = (Ax) · x does not imply A = AT.
(a) The statement is true. If (Ay)(A^T)y for all y in R^n, then A = A^T.
Proof: Let's consider an arbitrary vector y in R^n. We have:
(Ay)(A^T)y = (y^T A^T)(A^T y) = y^T(A^TA)y.
Since this holds for all y, we can conclude that (A^TA) = I, where I is the identity matrix.
Now, let's consider the transpose of both sides of the equation:
(A^TA)^T = I^T
(A^T)^T A^T = I
AA^T = I.
This implies that A^T is the inverse of A, and since A^T is the inverse of A, we can conclude that A = A^T.
(b) The statement is false. The property x · (Ax) = (Ax) · x for all x in R^n does not imply A = A^T.
The property x · (Ax) = (Ax) · x is known as the commutativity of the dot product. It states that the dot product of x with the result of applying A to x is the same as the dot product of the result Ax with x. However, this property does not provide any information about the relationship between A and its transpose A^T.
There are matrices A for which this property holds, but A is not equal to its transpose A^T. Therefore, the statement is disproved.
Learn more about Vector click here :brainly.com/question/13322477
#SPJ11
does anyone know?
Store A sells a watch for $50 and offers a 5% discount. Store B sells
a
the same watch for $60 and offers a 20% discount. From which store
should you buy, and why?
O Store B, $4.00 cheaper
O Store B, $9.50 cheaper
O Store A, $0.50 cheaper
O Store A, $9.50 cheaper
Answers
Answer:
(c) Store A, $0.50 cheaper
Step-by-step explanation:
When a price is discounted by a rate d, the multiplier of the price is (1 -d).
Store AThe discounted price is $50 × (1 -0.05) = $50×0.95 = $47.50
__
Store BThe discounted price is $60 × (1 -0.20) = $60×0.80 = $48.00
__
The price at Store A is less by ...
$48.00 -47.50 = $0.50
shop = 5 ÷ 100 × 50 = 2.5
shop = 20 - 60 × 100 = 12
shop = $50 - 2.5 = $ 47.5
Shop = $60 - 12 = $48
then, we have to minus $48 .00 with $ 47.50 we get :-= $48 .00 - $ 47.50 = $0.50
Store A, $0.50 cheaperCreate your own literal equation that contains distribution, addition/subtraetion, division, and at least 4 variables. Then chose a variable and solve your equation for it.
Answers
Answer:A combination of variables, numbers, and at least one operation.
Example: x+4
Step-by-step explanation:
