Drag and drop a statement or reason to each box to complete the proof. Given: parallelogram MNPQ Prove: ∠N≅∠Q Parallelogram M N P Q with diagonal M P drawn. Put responses in the correct input to answer the question. Select a response, navigate to the desired input and insert the response. Responses can be selected and inserted using the space bar, enter key, left mouse button or touchpad. Responses can also be moved by dragging with a mouse. Statement Reason parallelogram MNPQ Given MN¯¯¯¯¯¯¯≅QP¯¯¯¯¯MQ¯¯¯¯¯¯≅NP¯¯¯¯¯¯ Response area Response area Response area △MQP≅△PNM Response area Response area CPCTC


Answers
After solving the problems the answers obtained are MN ≅ QP and MQ ≅ NP, MP ≅ MP, Δ MQP ≅ Δ PNM, ∠ N ≅ ∠ Q.
What is Parallelogram?The phrase "parallelogram" is a translation of the Greek phrase "parallelogrammon," which means "bound by the contract by parallel lines." As a consequence, a quadrilateral that is bordered by parallel lines is called a parallelogram. It has parallel and equal opposite sides on all sides.
1. According to the parallelogram's feature that its opposed sides are congruent, the opposite sides of the given parallelogram MNPQ,
So, MN ≅ QP and MQ ≅ NP.
2. According to the reflexive feature of congruence, a line or other geometric figure is both a reflection of and consistent with itself. Therefore, in the example of the parallelogram MNPQ,
So,
MP ≅ MP
3. The SSS congruence postulate, which stands for Side-Side-Side congruence postulate, argues that when three adjacent sides of two triangles are congruent, the two triangles are congruent. As the sides MNQ, MQ, NP, and MP are in the given parallelogram MNPQ
Hence,
Δ MQP ≅ Δ PNM
4. Part 4 demonstrated that MQP and PNM are congruent, hence in accordance with a CPCTC property,
∠ N ≅ ∠ Q
5. The acronym CPCTC stands for congruent portions of congruent triangles.
To know more about Parallelogram:
https://brainly.com/question/19187448
#SPJ1
Related Questions
An average 1-year-old baby boy weighs around 9.6 kilograms. Convert this
weight into ounces.
Answers
Answer:
338.63 ounces
Step-by-step explanation:
1=35.274
35.274 times 9.6 is 338.6304
if the ratio of two sample variances exceeds the critical value of f at a defined confidence level, then___
Answers
if the ratio of two sample variances exceeds the critical value of f at a defined confidence level, then the level of confidence also exceeds the critical level.
All tests that make use of the F-distribution are collectively referred to as "F Tests." The F-Test to Compare Two Variances is often what is meant when the term "F-Test" is used. However, a number of tests, including regression analysis, the Chow test, and the Scheffe test, use the f-statistic. If we are conducting an F-Test, we might employ a variety of technological tools. since doing an F-test manually while accounting for variations is a difficult and time-consuming operation.
if the ratio of two sample variances exceeds the critical value of f at a defined confidence level, then the level of confidence also exceeds the critical level.
learn more about F-distribution,
https://brainly.com/question/13057442
#SPJ4
Find the critical value
χ2R
corresponding to a sample size of 5 and a confidence level of 99.0 percent
Answers
The critical value, given the sample size of 5 and the confidence level of 99. 0 percent would be 16. 812.
How to find the critical value ?The critical values for the chi-squared (χ^2) distribution depend on the degree of freedom and the level of significance.
The degree of freedom for a chi-squared distribution typically equals the sample size minus 1 so the degrees of freedom here is:
= 5 - 1
= 4
The level of significance would be:
= 1 - 99. 0 %
= 0. 01
The critical value of the sample would therefore be found on a chi -squared distribution table for df = 4 and α = 0.01 to be 16. 812.
Find out more on critical value at https://brainly.com/question/30536618
#SPJ1
The area of a rectangular window is 3816 cm
If the length of the window is 72 cm, what is its width
Answers
Answer: The width of the rectangular window is 53 cm.
Step-by-step explanation:
We know that the area of a rectangle is given by the formula:
Area = Length x Width
Substituting the given values, we have:
3816 cm² = 72 cm x Width
To solve for the width, we can divide both sides by 72 cm:
Width = 3816 cm² ÷ 72 cm
Width = 53 cm
Therefore, the width of the rectangular window is 53 cm.
In the 2002 - 2003 NBA regular season, the Sacramento Kings
won 13 more than twice as many games as they lost, The Kings
played 82 games. How many wins and losses did the team
mave?
Answers
Answer: Number of games lost = 23 and Number of games won = 59.
Step-by-step explanation:
Let x = Number of games lost, y = Number of games won.
y = 13 + 2x (i)
x+ y = 82 (ii)
Substitute value of y from (i) in (ii) , we get
x+ 13 + 2x = 82
⇒ 3x= 82-13
⇒ 3x = 69
⇒ x= 23 [Divide both sides by 3]
Put value of x in (i), y= 13+2(23) = 13+46=59
Hence, Number of games lost = 23 and Number of games won = 59.
suppose that during a test drive of two cars, one car travels 189 miles on the same time that a second car travels 135 miles. If the speed of the second car is 12 miles per hours faster than the speed of the second car, find the speed of both cars.
Answers
Main Answer: s1=42 mi/hr.
s2=30mi/hr.
Concept and definitions should be there:
Just as distance and displacement have distinctly different meanings (despite their similarities), so do speed and velocity. Speed is a scalar quantity that refers to "how fast an object is moving." Speed can be thought of as the rate at which an object covers distance. A fast-moving object has a high speed and covers a relatively large distance in a short amount of time. Contrast this to a slow-moving object that has a low speed; it covers a relatively small amount of distance in the same amount of time. An object with no movement at all has a zero speed.
Formula:
s = {d}/{t}
s=speed
d=distance traveled
t=time elapsed
Given data:
one car travels 189 miles on the same time that a second car travels 135 miles.
Solving part:
Let t be the amount of time the cars are traveling
s1=189/t and s2 = 135/t
We are told:
s1=s2+12
That is
189/t=135/t+12
Multiple t on both sides
⇒189 = 135+12t
⇒12t = 189-135
⇒12t = 54
⇒t = 4.5
s1 = 189/4.5
s1 = 42
s2 = 135/4.5
s2=30
Final Answer:s1=42 mi/hr.
s2=30mi/hr.
To learn about more about the speed visit:brainly.com/question/3328179 #SPJ9.
Use the definition to calculate the derivative of the following function. Then find the values of the derivative as specified.

Answers
Answer:
Refer to the step-by-step explanation, please follow along very carefully. Answers are encased in two boxes.
Step-by-step explanation:
Given the following function, find it's derivative using the definition of derivatives. Evaluate the function when θ=1, 11, and 3/11
\(p(\theta)=\sqrt{11\theta}\)
\(\hrulefill\)
The definition of derivatives states that the derivative of a function at a specific point measures the rate of change of the function at that point. It is defined as the limit of the difference quotient as the change in the input variable approaches zero.
\(f'(x) = \lim_{{h \to 0}} \dfrac{{f(x+h) - f(x)}}{{h}}\)\(\hrulefill\)
To apply the definition of derivatives to this problem, follow these step-by-step instructions:
Step 1: Identify the function: Determine the function for which you want to find the derivative. In out case the function is denoted as p(θ).
\(p(\theta)=\sqrt{11\theta}\)
Step 2: Write the difference quotient: Using the definition of derivatives, write down the difference quotient. The general form of the difference quotient is (f(x+h) - f(x))/h, where "x" is the point at which you want to find the derivative, and "h" represents a small change in the input variable. In our case:
\(p'(\theta) = \lim_{{h \to 0}} \dfrac{{p(\theta+h) - p(\theta)}}{{h}}\\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11(\theta + h)} - \sqrt{11\theta} }{h}\)
Step 3: Take the limit:
We need to rationalize the numerator. Rewriting using radical rules.
\(p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11(\theta + h)} - \sqrt{11\theta} }{h} \\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11\theta + 11h} - \sqrt{11\theta} }{h}\\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11}\sqrt{\theta+h} - \sqrt{11}\sqrt{\theta} }{h}\)
Now multiply by the conjugate.
\(p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11}\sqrt{\theta+h} - \sqrt{11}\sqrt{\theta} }{h} \cdot \dfrac{\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} }{\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} } \\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{(\sqrt{11}\sqrt{\theta+h} - \sqrt{11}\sqrt{\theta} )(\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} )}{h(\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} )} \\\\\\\)
\(\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{11h}{h(\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} )}\\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{11}{\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} }\)
Step 4: Simplify the expression: Evaluate the limit by substituting the value of h=0 into the difference quotient. Simplify the expression as much as possible.
\(p'(\theta)= \lim_{h \to 0} \dfrac{11}{\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{\sqrt{11}\sqrt{\theta+(0)} + \sqrt{11}\sqrt{\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{\sqrt{11}\sqrt{\theta} + \sqrt{11}\sqrt{\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{2\sqrt{11}\sqrt{\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{2\sqrt{11\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{2\sqrt{11\theta} }\)
\(\therefore \boxed{\boxed{p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta} }}}\)
Thus, we have found the derivative on the function using the definition.
It's important to note that in practice, finding derivatives using the definition can be a tedious process, especially for more complex functions. However, the definition lays the foundation for understanding the concept of derivatives and its applications. In practice, there are various rules and techniques, such as the power rule, product rule, and chain rule, that can be applied to find derivatives more efficiently.\(\hrulefill\)
Now evaluating the function at the given points.
\(p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta}}; \ p'(1)=??, \ p'(11)=??, \ p'(\frac{3}{11} )=??\)
When θ=1:
\(p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta}}\\\\\\\Longrightarrow p'(1)= \dfrac{\sqrt{11} }{2\sqrt{1}}\\\\\\\therefore \boxed{\boxed{p'(1)= \dfrac{\sqrt{11} }{2}}}\)
When θ=11:
\(p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta}}\\\\\\\Longrightarrow p'(11)= \dfrac{\sqrt{11} }{2\sqrt{11}}\\\\\\\therefore \boxed{\boxed{p'(11)= \dfrac{1}{2}}}\)
When θ=3/11:
\(p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta}}\\\\\\\Longrightarrow p'(\frac{3}{11} )= \dfrac{\sqrt{11} }{2\sqrt{\frac{3}{11} }}\\\\\\\therefore \boxed{\boxed{p'(\frac{3}{11} )= \dfrac{11\sqrt{3} }{6}}}\)
Thus, all parts are solved.
Explain how to use patterns or sequences to determine the last digit of the number 7N, where N is the four-digit year of your birth.
Answers
differenciate the Function 1/ X3
Answers
Step-by-step explanation:
To differentiate the function f(x) = 1/x^3, we can use the power rule of differentiation. Here's the step-by-step process:
Write the function: f(x) = 1/x^3.
Apply the power rule: For a function of the form f(x) = x^n, the derivative is given by f'(x) = nx^(n-1).
Differentiate the function: In our case, n = -3, so the derivative is:
f'(x) = -3 * x^(-3-1) = -3 * x^(-4) = -3/x^4.
Therefore, the derivative of the function f(x) = 1/x^3 is f'(x) = -3/x^4.
1/3 of 3/7=__
pls i need help
Answers
Answer:
the answer is 0.14285714285 theres whole answer because i dont know if u need it rounded or not
Step-by-step explanation:
the bitly stuff is not real
based on the table, do the data support the use of a normal model to approximate population characteristics?
Answers
Yes, as the relative frequency distribution closely resembles the empirical criterion for normal models.
Frequency tables or charts are used to represent frequency distributions. Frequency distributions can display the proportion of observations or the actual number of observations that fall inside each range. The distribution is known as a relative frequency distribution in the latter case.
What is the relative frequency distribution formula?
Subgroup Count / Total Count: Relative Frequency
Because they let us determine how frequent a certain value is in a dataset in comparison to all other values, relative frequency distributions are helpful.
Know more about Relative Frequency
https://brainly.com/question/3857836
#SPJ4
Write the statement in words. Let p="The plane is on time." Let q="The sky is clear."
Q->~P

Answers
The statement can be read as "If the sky is clear, then the plane is not on time."
What is the conditional statement?
A conditional statement is a logical statement that has two parts: an antecedent (also called a hypothesis) and a consequent (also called a conclusion). The statement asserts that if the antecedent is true, then the consequent must also be true.
The statement "Q -> ~P" is an example of a conditional statement in symbolic logic.
In this case, Q represents "The sky is clear" and ~P represents "The plane is not on time" (the tilde symbol ~ negates the truth value of P).
The arrow symbol -> means "implies" or "if...then". Therefore, the statement can be read as "If the sky is clear, then the plane is not on time."
In other words, the statement is saying that if the sky is clear, then it is not possible for the plane to be on time.
This is because the statement implies that the plane being on time is dependent on the sky not being clear. So if the sky is clear, it means that the conditions for the plane to be on time are not present, and therefore the plane is not on time.
It's worth noting that the statement does not say anything about what happens if the sky is not clear.
It's possible that the plane could still be on time even if the sky is not clear, according to this statement.
Hence, the statement can be read as "If the sky is clear, then the plane is not on time."
To learn more about the conditional statement visit:
https://brainly.com/question/27839142
#SPJ1
Brainliest for correct awnser Estimate the line of best fit using two points on the line.A.y = −8x + 80B.y = 4x + 80C.y = −4x + 80D.y = 8x + 80

Answers
Answer:
A.y = −8x + 80B
Step-by-step explanation:
first you have to find the slope :
P1(2,64). P2(6,32)
slope=Y2-Y1/X2-X1
slope=64-32/2-6
slope= -8
y= -8x + b. now solve for "b" by using one of the coordinates given above.
y= -8x + b. I will use coordinate p(2,64)
64= -8(2) + b
64 + 16 = b
80= b
you can use any of the coordinates i.e either P1(2,64)or P2(6,32) it doesn't affect the value of "b".
line of equation is :
.y = −8x + 80B
Answer: y= -8x+80
Step-by-step explanation:
a movie premiere had a full house at 350 film Buffs the price of the tickets were $6 for adults and $4 for underage the income from ticket sales was $1,600 what is the number of adult x who attended
Answers
The residents of a city voted on whether to raise property taxes. The ratio of yes votes to no votes was 5 to 8. If there were 9854 total votes, how many no votes were there?
Answers
There were approximately 6056 no votes.
Let's assume the number of yes votes is represented by the variable "5x," where x is a positive constant.
Similarly, the number of no votes can be represented by "8x" since the ratio of yes votes to no votes is 5 to 8.
The total number of votes is given as 9854, so we can set up the following equation:
\(5x + 8x = 9854\)
Combining like terms, we have:
\(13x = 9854\)
To solve for x, we divide both sides of the equation by 13:
\(x = \frac{9854 }{13}\)
\(x \approx 757.23\)
Since x represents a positive constant, we round it to the nearest whole number, giving us x = 757.
Now, we can find the number of no votes by multiplying x by the ratio of no votes:
No votes \(= 8x\)
\(= 8 \times 757\)
\(= 6056\)
Therefore, there were approximately 6056 no votes.
For such more questions on votes
https://brainly.com/question/32031211
#SPJ8
one millon divide by 473.8
Answers
Answer:23(22.95684113865932)
Step-by-step explanation:
1. A recipe for corn chowder makes one hundred and fifty 6-ounce servings. You will be making
forty 8-ounce servings. What is the recipe conversion factor?
Answers
Answer: 16/45 or .355 is the recipe conversation factor
Step-by-step explanation:
150×6=900
40×8= 320
320/900 = 16/45 or 0.355
Figure out what the total amount of ounces the original recipe will make. Then the total amount you need to make. Set up a proportion of the needed amount to the original amount.
You will multiply each original mesurement in the original by the conversation factor to get the measurements you need.
Trigonometry: Measure tal Excel In Opt. Mathematics - Book 9 ) If the number of degrees of a certain angle added to the number of gra same angle is 152, find the angle in degrees.
Answers
The angle in degrees is 873.1843.
Let the measure of the angle be θ in degrees. Therefore, the measure of the same angle in gradians is (θ × π/180).
According to the given information, the number of degrees of a certain angle added to the number of gradians of the same angle is 152.(θ) + (θ × π/180) = 152.
Simplifying the above equation, we get:(θ) + (θ/180 × π) = 152.
Multiplying both sides of the equation by 180/π, we get:
θ + θ = (152 × 180)/π2θ = (152 × 180)/πθ = (152 × 180)/(3.14)θ = 873.1843
Thus, the angle in degrees is 873.1843.
For more such questions on angle, click on:
https://brainly.com/question/25770607
#SPJ8
Answer question number 20. The question is in the image.


Answers
Answer:
• Amplitude: 0.5
,• Period: 0.5
Explanation:
Given the function:
\(g(x)=\frac{1}{2}\cos(4\pi x)\)Amplitude
The amplitude of the general cosine function of the form y=Acos(Bx+C)+D is A.
Therefore, the amplitude of g(x) is 0.5.
Period
The period of the general cosine function of the form y=Acos(Bx+C)+D is determined using the formula:
\(Period=\frac{2\pi}{|B|}\)From g(x), the value of B = 4π, therefore:
\(Period=\frac{2\pi}{|4\pi|}=\frac{1}{2}\)Graph
The graph of g(x) is given below:
Transformation
The parent function y=cos(x) has been vertically compressed by a factor of 1/2 and horizontally compressed by a factor of 4π.

Andre and Noah started tracking their savings at the same time. Andre started with $15 and deposits $5 per week. Noah started with $2.50 and deposits $7.50 per week. The graph of Noah's savings is given and his equation is y=7.5x+2.5, where x represents the number of weeks and y represents his savings.
1. Write the equation for Andre's savings.
2. Graph it alongside Noah's.
3. What does the intersection point mean in this situation?
Answers
Answer:
1. he started with 15 and 5 per week. w is week
a is andre
a = 15 + 5w
Step-by-step explanation:
Answer: 1. Y= 5x + 15
2. Start at 15 and go up 5
3.when they both had the same amount of money at the same time
Step-by-step explanation:
Merrisa is booking a holiday costing £660.
She needs to pay a deposit of of the total cost of the booking
How much does she pay?
Answers
The amount of money she will have to pay for booking of the holidays would be = £220
How to calculate the amount ofr deposit?The total amount of money that will cost Merrisa for booking of holidays = £660
The fraction of the total cost that she needs to deposit = 1/3
Therefore, the actual amount that she needs to deposit = 1/3 of £660
= 1/3× 660
= £220
Therefore, in conclusion, Merrisa would have to pay a total of £220 for booking of the holidays. This total amount is ⅓ of total cost of booking.
Learn more about division here:
https://brainly.com/question/25289437
#SPJ1

-4 2/3 • 1 4/5
Help me with this
Answers
the answer is -42/5 :D
can't type because im lazy

help 50 brainly for first answer

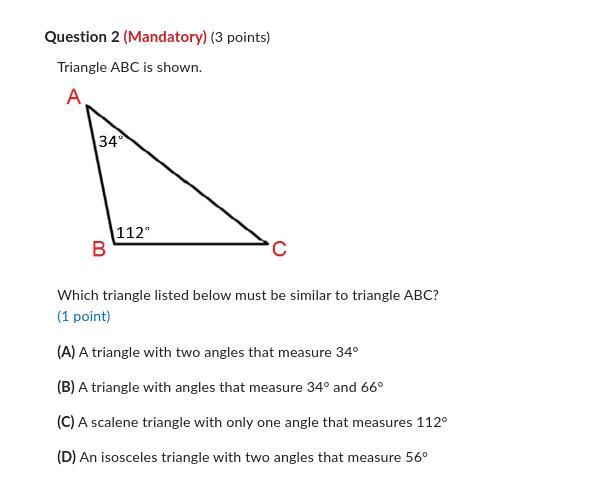


Answers
Answer: B
Step-by-step explanation:
X ~ N(70, 14). Suppose that you form random samples of 25 from this distribution. Let X be the random variable of averages. Let ?X be the random variable of sums. Find the 10th percentile. (Round your answer to two decimal places.)
Answers
Answer:
The 10th percentile is 66.42.
Step-by-step explanation:
To solve this question, we need to understand the normal probability distribution and the central limit theorem.
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
X ~ N(70, 14).
This means that \(\mu = 70, \sigma = 14\)
Suppose that you form random samples of 25 from this distribution.
This means that \(n = 25, s = \frac{14}{\sqrt{25}} = 2.8\)
Find the 10th percentile.
This is X when Z has a pvalue of 0.1, so X when Z = -1.28.
\(Z = \frac{X - \mu}{\sigma}\)
By the Central Limit Theorem
\(Z = \frac{X - \mu}{s}\)
\(-1.28 = \frac{X - 70}{2.8}\)
\(X - 70 = -1.28*2.8\)
\(X = 66.42\)
The 10th percentile is 66.42.
The following dataset represents the salaries for all six employees at a small start-up company. Find the mean, variance, and standard deviation for this dataset of salaries (expressed in thousands of dollars): 55, 59, 63, 67, 71,75 (Round your answers to one decimal place) Select the correct answer below: O Mean - 65.0, Standard Deviation = 7.2. Variance - 49.9 O Mean - 65.0, Standard Deviation = 6.8. Variance - 46.7 O Mean - 67.0, Standard Deviation = 6.8. Variance = 46.7 O Mean 65.0, Standard Deviation - 9.8. Variance - 46.7
Answers
The correct answer is option B i.e. Mean - 65.0, Standard Deviation = 6.8. Variance - 46.7.
What exactly is mean?
Mean, also known as arithmetic mean, is a statistical measure of central tendency that is calculated by summing up all the values in a dataset and then dividing the sum by the total number of values. It is often used to represent the "typical" value or central value of a dataset. Mean is one of the most commonly used measures of central tendency, along with median and mode.
Now,
From given dataset 55, 59, 63, 67, 71,75
Mean = (55 + 59 + 63 + 67 + 71 + 75) / 6 = 65
Variance = [(55-65)² + (59-65)² + (63-65)² + (67-65)² + (71-65)² + (75-65)²] / 6 = 46.7
Standard deviation = √(Variance) = √(46.7) ≈ 6.8
Therefore, the correct answer is: Mean - 65.0, Standard Deviation = 6.8. Variance - 46.7
To know more about Mean visit the link
https://brainly.com/question/30112112?referrer=searchResults
#SPJ1
To find the value of an expression is to what?
A) Variable
B) squared
C) evaluate
D) algebra
Answers
Answer:
evaluate
Step-by-step explanation:
um duh
but I hope I helped in some way
The Arc Electronic Company had an income of 59 million dollars last year. Suppose the mean income of firms in the same industry as Arc for a year is 45 million dollars with a standard deviation of 7 million dollars. If incomes for this industry are distributed normally, what is the probability that a randomly selected firm will earn more than Arc did last year
Answers
Answer:
0.0228 = 2.28% probability that a randomly selected firm will earn more than Arc did last year
Step-by-step explanation:
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Suppose the mean income of firms in the same industry as Arc for a year is 45 million dollars with a standard deviation of 7 million dollars
This means that \(\mu = 45, \sigma = 7\)
What is the probability that a randomly selected firm will earn more than Arc did last year?
Arc earned 59 million, so this is 1 subtracted by the pvalue of Z when X = 59.
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{59 - 45}{7}\)
\(Z = 2\)
\(Z = 2\) has a pvalue of 0.9772
1 - 0.9772 = 0.0228
0.0228 = 2.28% probability that a randomly selected firm will earn more than Arc did last year
URGENT!!! Find the surface area of the regular pyramid to the nearest hundredth.

Answers
Answer:
632.83mm²
Step-by-step explanation:
Applying Pythagorean theorem to triangle SOH
SH² = SO² + OH²
SH = \(\sqrt{(15.4)^2+(7.2)^2}=17mm\)
Since the base of the pyramid is a regular pentagon, angle OAH
is 108°/2 = 54°.
AH = 7.2/tan 54° = 5.23mm
So AB = 2AH = 10.46mm
The area of triangle SAB is:
A1 = 1/2 × SH × AB = 1/2 × 17 × 10.46 = 88.91mm²
The area of all triangles is
A2 = 5 × A1 = 5 × 88.91 = 444.55mm²
The area of the base is:
A3 = (perimeter × apothem)/2 = (5 × 10.46 × 7.2)/2 = 188.28mm²
The surface area of the pyramid is:
A2 + A3 = 444.55 + 188.28 = 632.83mm²

Step-by-step explanation:
the surface area is the sum of the base area (pentagon) and the 5 side triangles (we only need to calculate one and then multiply by 5, as they are all equal).
these side triangles are isoceles triangles (the legs are equally long).
the usual area formula for a pentagon is
1/2 × perimeter × apothem
the apothem is the minimum distance from the center of the pentagon to each of its sides.
in our case this is 7.2 mm.
how to get the perimeter or the length of an individual side of the pentagon ?
if the apothem of a pentagon is given, the side length can be calculated with the formula
side length = 2 × apothem length × tan(180/n)
where 'n' is the number of sides (5 in our case). After getting the side length, the perimeter of the pentagon can be calculated with the formula
perimeter = 5 × side length.
so, in our case
side length = 2 × 7.2 × tan(180/5) = 14.4 × tan(36) =
= 10.4622124... mm
perimeter = 5 × 10.4622124... = 52.31106202... mm
area of the pentagon = 1/2 × perimeter × apothem =
= 1/2 × 52.31106202... × 7.2 = 188.3198233... mm²
now for the side triangles.
the area of such a triangle is
1/2 × baseline × height
baseline = pentagon side length
height we get via Pythagoras from the inner pyramid height and the apothem :
height² = 7.2² + 15.4² = 51.84 + 273.16 = 289
height = 17 mm
area of one side triangle =
1/2 × 10.4622124... × 17 = 88.92880543... mm²
all 5 side triangles are then
444.6440271... mm²
and the total surface area is then
444.6440271... + 188.3198233... = 632.9638504... mm²
≈ 632.96 mm²
WRITE THE PRODUCT AS THE PRODUCT OF A
WHOLE NUMBER AND A UNIT FRACTION
2 x 5/8
Answers
Answer:
Step-by-step explanation:
When you multiply a whole number by a fraction, you multiply the whole number by the numerator (top) of the fraction and you end up with an improper fraction. This question simply wants you to multiply the whole number by the numerator, then multiply that whole number by the remaining fraction.
= 4 * 2/6
multiply 4 by the numerator
=(4*2)/6
multiply 4*2 then separate from the remaining 1/6 fraction
=8 * 1/6
ANSWER: 8 * 1/6
Hope this helps! :)
This graph represents the flight path of a model rocket launched in a park.
What do the key features of the curve represent in terms of the flight path of the rocket?
Chose from the drop-down to match each situation.
ill give brainlyest to the first to correctly answer this

Answers
The drop down menu is used to match each situation as below.
1. The rocket reached its maximum the x-value of the vertex
height in 5 s.
2. ground level the y-intercept
3. The rocket launcher was the y-value of the point containing
on the ground. the x-intercept on the right
4. The rocket was in the air 10 the x-intercept on the right
5. The maximum height of the the y-value of the vertex
rocket is 50 ft.
6. the time the rocket was the x-value of the point containing the
launched y-intercept
What is the key feature of the curveThe key features of the curve such as the x intercept is the point the launcher and the rocket were on ground.
The vertex is the point the rocket had the maximum and height.
Generally, the curve traces a parabolic path
Learn more about parabolic equation at
https://brainly.com/question/4061870
#SPJ1