Answers
Answer:
what do we evaluate the picture is all blurry and won't show up
Related Questions
You are washing cars over the summer. It costs you $3 to wash each car and a one-time cost of $35 for some supplies to market your car wash. You plan to charge $10 per wash. Write an equation and solve to determine the amount of cars you need to break even.
Answers
The amount of cars you need to break even is 5.
To determine the number of cars you need to break even, we can set up an equation where the revenue equals the total cost.
Let's denote the number of cars as x.
Revenue = Number of cars × Price per wash
= x × $10
Total cost = Cost per car × Number of cars + One-time cost
= $3x + $35
To break even, the revenue should be equal to the total cost:
x × $10 = $3x + $35
Now, let's solve this equation to find the value of x:
10x = 3x + 35
Subtract 3x from both sides:
10x - 3x = 3x + 35 - 3x
7x = 35
Divide both sides by 7:
x = 35 / 7
x = 5
For similar questions on amount
https://brainly.com/question/24644930
#SPJ11
A consumer group has determined that the distribution of life spans for gas ovens has a mean of 15.0 years and a standard deviation of 4.2 years. The distribution of life spans for electric ovens has a mean of 13.4 years and a standard deviation of 3.7 years. Both distributions are moderately skewed to the right. Suppose we take a simple random sample of 35 gas ovens and a second simple random sample of 40 electric ovens. Suppose we take a simple random sample of 35 gas ovens and a second SRS of 40 electric ovens. Which of the following best describes the sampling distribution of barXG - bar XE, the difference in mean life span of gas and electric ovens?
A. Mean = 1.6 years, standard deviation = 7.9 years, shape: moderately right-skewed.
B. Mean = 1.6 years, standard deviation = 0.92 years, shape: approximately Normal.
C. Mean = 1.6 years, standard deviation = 0.92 years, shape: moderately right skewed.
D. Mean = 1.6 years, standard deviation = 0.40 years, shape: approximately Normal.
E. Mean = 1.6 years, standard deviation = 0.40 years, shape: moderately right skewed.
Answers
Answer:
B. Mean = 1.6 years, standard deviation = 0.92 years, shape: approximately Normal.
Step-by-step explanation:
To solve this question, we need to understand the normal probability distribution and the central limit theorem.
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
Subtraction of normal variables:
When we subtract normal variables, the mean is the subtraction of the means, while the standard deviation is the square root of the sum of the variances.
35 gas ovens
A consumer group has determined that the distribution of life spans for gas ovens has a mean of 15.0 years and a standard deviation of 4.2 years. This means that:
\(\mu_G = 15, \sigma_G = 4.2, n = 35, s_G = \frac{4.2}{\sqrt{35}} = 0.71\)
40 electric ovens.
The distribution of life spans for electric ovens has a mean of 13.4 years and a standard deviation of 3.7 years.
\(\mu_E = 13.4, \sigma_E = 3.7, n = 40, s_E = \frac{3.7}{\sqrt{40}} = 0.585\)
Which of the following best describes the sampling distribution of barXG - bar XE, the difference in mean life span of gas and electric ovens?
By the Central Limit Theorem, the shape is approximately normal.
Mean: \(\mu = \mu_G - \mu_E = 15 - 13.4 = 1.6\)
Standard deviation:
\(s = \sqrt{s_G^2+s_E^2} = \sqrt{(0.71)^2+(0.585)^2} = 0.92\)
So the correct answer is given by option b.
Find the rule. Input: 72,54,120,360,84 Output: 12,9,20,60,14 Rule: Use the rule to find the Output if the Input is 150.
Answers
Answer:
If Input is 150, then Output is 25.
Step-by-step explanation:
The rule is to divide 6.
IF: You input 72 & the output is 12:
72/6 = 12
IF: You input 54 & the output is 9:
54/6 = 9
IF: You input 120 & the output is 20:
120/6 = 20
etc.
Therefore, you are dividing 6 each time. The given input is 150. Divide 150 with 6 to find your output:
150/6 = 25
25 would be your output.
~
Learn more about solving divisions, here:
https://brainly.com/question/21416852
true-false questions: justify your answers. 1.13 the solution set to a system of three equations in three unknowns cannot be a plane. 1.14 a system of linear equations cannot have only two solutions. 1.15 the solution set to a consistent rank 2 linear system in four unknowns would be a line in four-dimensional space. 1.16 a system of four equations in four unknowns always has a solution. 1.17 a system of four equations in four unknowns can have at most one solution. 1.18 the rank of a system is always less than or equal to the number of equations in the system. 1.19 use geometric reasoning to answer the following questions concerning systems (i) and (ii) below: (a) if (i) has exactly one solution, then the same is true for (ii). (b) if the solution set of (i) is a line, then the same is true for (ii). (c) if (i) has no solutions, then the same is true for (ii). (i) a1x b1y c1z
Answers
The True- False of given statements of Solutions of Equations are justified.
1.13 False. The solution set to a system of three equations in three unknowns can be a point, a line, or a plane. It depends on the system of equations and how they intersect in three-dimensional space.
1.14 False. A system of linear equations can have infinitely many solutions, one solution, or no solutions. It depends on the coefficients of the equations and the rank of the coefficient matrix.
1.15 False. The solution set to a consistent rank 2 linear system in four unknowns would be a plane in four-dimensional space, not a line.
1.16 False. A system of four equations in four unknowns may not have a solution, or it may have infinitely many solutions or one solution. It depends on the coefficients of the equations and the rank of the coefficient matrix.
1.17 False. A system of four equations in four unknowns can have infinitely many solutions or one solution, but it cannot have at most one solution.
1.18 True. The rank of a system is always less than or equal to the number of equations in the system.
1.19 (a) False. If (i) has exactly one solution, it does not necessarily mean that (ii) will have exactly one solution. It depends on the coefficients of the equations in (ii).
(b) False. If the solution set of (i) is a line, it does not necessarily mean that the same is true for (ii). It depends on the coefficients of the equations in (ii).
(c) True. If (i) has no solutions, then the same is true for (ii), since (ii) is equivalent to (i).
To know more about Solutions of Equations:
https://brainly.com/question/29757556
#SPJ4
29. Assertion :7√5, √2+21 are the irrational number. Reason: every integer is an rational number 30.
Answers
The assertion is true. Both 7√5 and √2 + 21 are irrational numbers because they cannot be expressed as fractions.
The assertion is true. Both 7√5 and √2 + 21 are irrational numbers.
An irrational number is defined as a number that cannot be expressed as a fraction of two integers and has an infinite non-repeating decimal representation.
In the case of 7√5, the square root of 5 is an irrational number because it cannot be expressed as a fraction. Multiplying it by 7 does not change its irrational nature.
Similarly, √2 is also an irrational number because the square root of 2 cannot be expressed as a fraction. Adding 21 to √2 does not alter its irrationality.
The reason provided, that every integer is a rational number, is not relevant to the given assertion. While it is true that every integer is a rational number because it can be expressed as a fraction (e.g., 3 can be written as 3/1), it does not contradict the fact that 7√5 and √2 + 21 are irrational numbers.
In conclusion, the assertion is valid, and both 7√5 and √2 + 21 are irrational numbers.
For more questions on fractions
https://brainly.com/question/78672
#SPJ8
I dont get this question could someone help me out i will mark brainliest include steps!

Answers
Answer:
12.5
Step-by-step explanation:
In a rectangle, the two diagonals are equal length, so MK = JL = 2x + 9
Note MK = 2 * MN, so
2x + 9 = 2 * (3x + 1)
expand:
2x + 9 = 6x + 2
Solve:
9 - 2 = 6x - 2x
4x = 7
x = 7/4
MK = JL = 2x + 9 = 2 * 7/4 + 9 = 7/2 + 9 = 3.5 + 9 = 12.5
find the following answer

Answers
Cardinality of given set is 10.
Describe Cardinality.The cardinality of a mathematical set refers to the number of entries in the set. It may be limited or limitless. For instance, if set A has six items, its cardinality is equivalent to 6: 1, 2, 3, 4, 5, and 6. A set's size is often referred to as the set's cardinality. The modulus sign is used to indicate it on either side of the set name, |A|.
a Set's CardinalityA set that can be counted and has a finite number of items is said to be finite. On the other hand, an infinite set is one that has an unlimited number of components and can either be countable or uncountable.
Possible set of A=14+4+1+9=28
Possible set of C=1 +6+9+9=25
n(A∩ C)=10
Hence, Cardinality of given set is 10.
To know more about modulus, visit:
https://brainly.com/question/10737199
#SPJ1
In a recent snail race, the winning snail traveled 5.85 cm in 3/4 of a minute. How fast was the snail traveling in centimeters per second?
Answers
The Snail traveling in the race will be 0.13 centimeters per second.
What is Algebra?Algebra is the study of abstract symbols, while logic is the manipulation of all those ideas.
Speed is defined as the length traveled by a particle or entity in an hour. It is a scale parameter. It is the ratio of length to duration.
We know that the speed formula
Speed = Distance/Time
In a new snail race, the triumphant snail voyaged 5.85 cm in 3/4 of a moment.
Convert time into seconds, then we have
T = 3/4 x 60
T = 45 seconds
The speed of the snail in the race will be given as,
Speed = 5.85 / 45
Speed = 0.13 cm per second
The Snail traveling in the race will be 0.13 centimeters per second.
More about the Algebra link is given below.
https://brainly.com/question/953809
#SPJ1
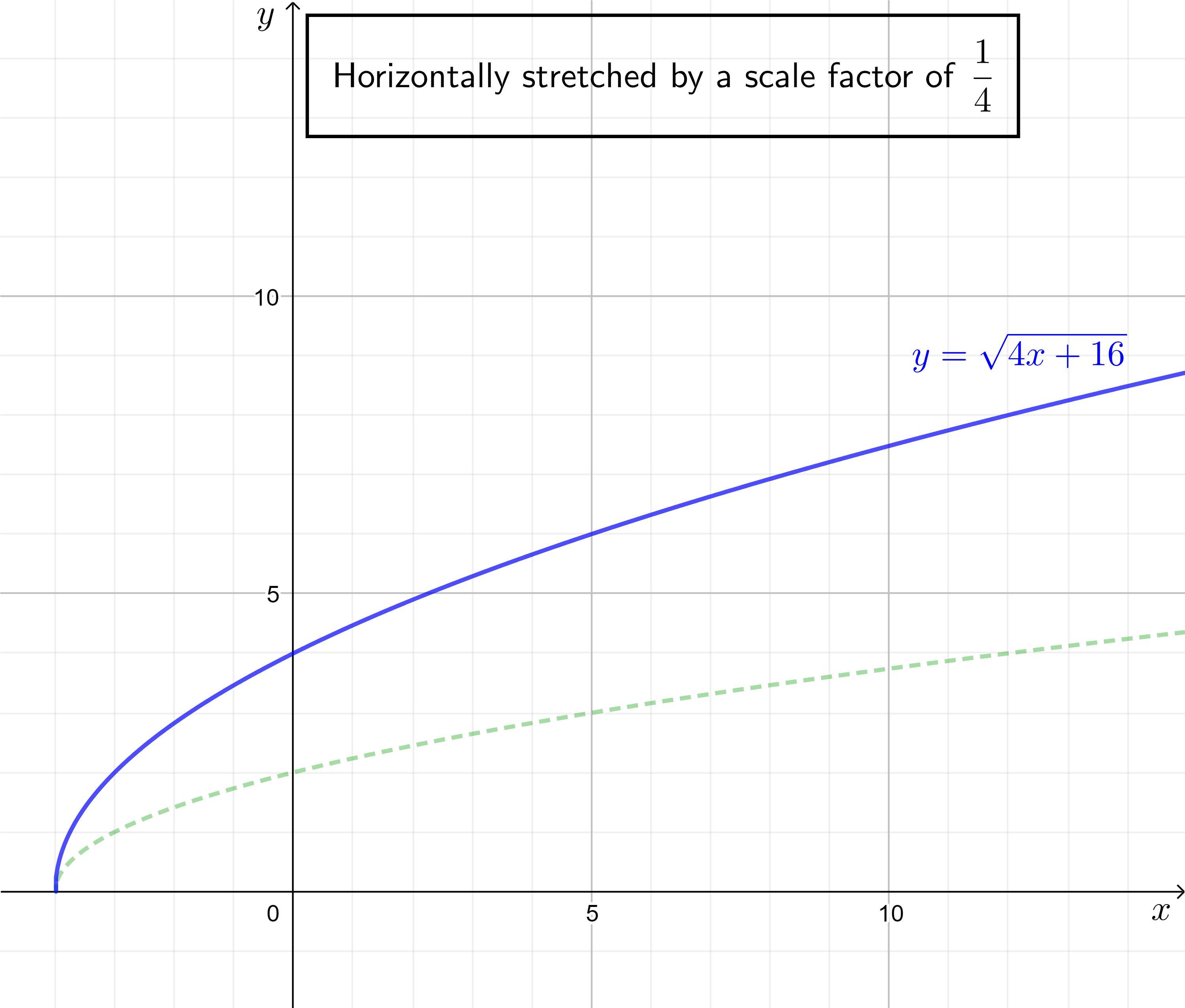
. Rewrite Y = √4x+16 +5 y to make it easy to graph using a translation. Describe the graph.
Answers
Answer:
The graph of \(y=\sqrt{4x+16}+5\) is the graph of \(y=\sqrt{x}\) translated 4 units left, stretched horizontally by a factor of 1/4, and translated 5 units up.
Step-by-step explanation:
Transformations
\(\textsf{For }a > 0\)
\(f(x+a) \implies f(x) \: \textsf{translated}\:a\:\textsf{units left}\)
\(f(x)+a \implies f(x) \: \textsf{translated}\:a\:\textsf{units up}\)
\(y=f(ax) \implies f(x) \: \textsf{stretched parallel to the x-axis (horizontally) by a factor of} \: \dfrac{1}{a}\)
Given function
\(y=\sqrt{4x+16}+5\)
Parent function
Parent functions are the simplest form of a given family of functions.
\(y=\sqrt{x}\)
The graph of the parent function is related to the graph of the given function by a series of transformations. To determine the series of transformations, work out the steps of how to go from the parent function to the given function.
Factor the expression under the square root sign:
\(y=\sqrt{4(x+4)}+5\)
Transformations
Parent function:
\(f(x)=\sqrt{x}\)
Translated 4 units left:
\(f(x+4)=\sqrt{x+4}\)
Horizontally stretched by a factor of 1/4 (compressed by a factor of 4):
\(\begin{aligned}f(4(x+4)) & =\sqrt{4(x+4)}\\ & = \sqrt{4x+16} \end{aligned}\)
Translated 5 units up:
\(f(4x+16)+5=\sqrt{4x+16}+5\)
Therefore, the graph of \(y=\sqrt{4x+16}+5\) is the graph of \(y=\sqrt{x}\) translated 4 units left, stretched horizontally by a factor of 1/4, and translated 5 units up.
Learn more about graph transformations here;
https://brainly.com/question/27962370
https://brainly.com/question/27975349



According to Wikipedia, the following are the lengths of terms of the US Presidents that preceded Joe Biden. There is a total of 44. You may have expected to see a total of 45, as Biden is the 46th us President, but Grover Cleveland was considered the 22nd and the 24th President, but is only counted once in this list The 2922 is the length of two full terms and the 1461 is the length of one full term FDR, the 4422 in the table, had actually started his FOURTH term before dying in office The 31 is William Henry Harrison who became ill shortly after his inauguration. His death may have been due to pneumonia Number of US Presidents 12 1 1 Term in Days 4422 2922 2865 2.840 2.728 2.041 2.027 1.886 1,654 1.503 1,461 1.460 1.430 1.419 1 1 12 1 1 1.419 1.262 1,036 969 895 881 492 199 31 TOTAL: 1 1 1 1 1 1 1 1 1 44 Determine the mean, median and mode for this set of data Give each to the nearest whole day Mean = Median = Mode = and With one of the modes being a high value as well as the term of FDR being much higher than all others, was pulled up to a higher value than another of hte measures of central tendency the
Answers
The mean of the given data is 1744 days, median of the given data is 1460.5 days, mode of the given data is 1461 days & 4422 days.
To find the mean, median, and mode of the lengths of terms of the US Presidents that preceded Joe Biden:
Mean:
To find the mean, we add up all of the term lengths and divide by the total number of terms:
Mean = (4422 + 2922 + 2865 + 2840 + 2728 + 2041 + 2027 + 1886 + 1654 + 1503 + 1461 + 1460 + 1430 + 1419 + 1262 + 1036 + 969 + 895 + 881 + 492 + 199 + 31) / 44
Mean = 1743.77 days
Median:
To find the median, we need to arrange the term lengths in order from smallest to largest, and then find the middle term. In this case, since we have an even number of terms, we will take the average of the two middle terms:
31 199 492 881 895 969 1036 1262 1419 1430 1460 1461 1503 1654 1886 2027 2041 2728 2840 2865 2922 4422
Median = (1460 + 1461) / 2
Median = 1460.5 days
Mode:
The mode is the most frequently occurring term length. In this case, there are two modes: 1,461 days and 4,422 days.
Since the term length of FDR is much higher than all the other term lengths, it has pulled up the mean to a higher value than the other measures of central tendency. Additionally, the mode being a high value is likely due to the fact that FDR served for more than three terms, which is an outlier in the data set.
For more such questions on Mean & median
https://brainly.com/question/26177250
#SPJ4
Please help! Correct answer only, please! The cafeteria manager at a middle school wanted to keep track of how many student breakfast and lunches were sold on a Monday. A. B. C. D.

Answers
Answer:
Hello There Again. The Correct answer is C.
Explanation: Because it shows that the numbers need to be least median then greater of the breakfast lunch.
Hope It Helps! :)
Split 84 into two parts so that one part is five times the other part.
Answers
Answer:
x+5x=84
6x=84
6x/6=84/6
x=14
so therefore
14+5(14)
14+70
The numbers are 14 and 70
The two parts are x = 70 and y = 14
We have a 2 - digit number - 84.
We have to split it into two parts such that one part is five times the other part.
Divide 24 into two parts such that second part is 3 times the first part.Assume the two numbers to be x and y.
x + y = 24
A/Q -
y = 3x
x + 3x =24
4x = 24
x = 6
and y = 3 x 6 = 18.
According to question, we have -
Number = 84
Assume the first part be x.
Then, the other part = \(\frac{x}{5}\)
Therefore -
x + \(\frac{x}{5}\) = 84
5x + x = 84 x 5
6x = 420
x = 70
and
y = \(\frac{x}{5} =\frac{70}{5}\) = 14
Hence, the two parts are x = 70 and y = 14
To solve more questions on Splitting Number, visit the link below -
https://brainly.com/question/16766926
#SPJ2
What is the surface area?
2 yd
7 yd
6 yd
square yards:
Actually get the answer and you get Brainlyest

Answers
Answer:
total surface area = 136 yd
Step-by-step explanation:
Answer:
For a rectangular prism use this formula to find the surface area:
SA of rectangular prism = 2(lw + wh + lh), where, l is length, w is width and h is the height of the prism.
Now, let's input our numbers given into the equation.
SA = 2(7×6 + 6×2 + 7×2)
Okay, so now that we have an equation filled out, let's solve to find the Surface Area of this rectangular prism.
SA = 2(7×6 + 6×2 + 7×2)
SA = 136 square yards
Step-by-step explanation:
If any questions please put them below.
The value of x in this system of equations is 1.
3x + y = 9
y = -4x + 10
Substitute the value of y in the first equation:
Combine like terms:
Apply the subtraction property of equality:
Apply the division property of equality:
3x + (-4x + 10) = 9
-X + 10 = 9
X
What is the value of y?
Answers
Answer:
y = 6
Step-by-step explanation:
y = -4(1) + 10 = -4 + 10 = 6
Find all the two-digit numbers that decrease 12 times when the last digit is crossed out.
Answers
Answer:
Step-by-step explanation:
If function f is vertically stretched by a factor of 2 to give function g, which of the following functions represents function g?

Answers
The transformation of a function may involve any change in the function. The value of the function g(x) will be 6|x|+10.
How does the transformation of a function happen?The transformation of a function may involve any change.
Usually, these can be shifted horizontally (by transforming inputs) or vertically (by transforming output), stretched (multiplying outputs or inputs) etc.
If the original function is y = f(x), assuming the horizontal axis is the input axis and the vertical is for outputs, then:
Horizontal shift (also called phase shift):
Left shift by c units, y=f(x+c) (same output, but c units earlier)
Right shift by c units, y=f(x-c)(same output, but c units late)
Vertical shift
Up by d units:
Down by d units: y = f(x) - d
Stretching:
Vertical stretch by a factor k: y = k \times f(x)
Horizontal stretch by a factor k: y = f(\dfrac{x}{k})
Given the function f(x)=3|x|+5, therefore, if the function is vertically stretched by a factor of 2, then the function g(x) can be written as,
g(x) = 2[f(x)]
g(x) = 2(3|x|+5)
g(x) = 6|x| + 10
Hence, the value of the function g(x) will be 6|x|+10.
Learn more about Transforming functions:
https://brainly.com/question/17006186
#SPJ1
I need to know what is in the process box, it goes with the formula y=mx+b

Answers
Answer:
y= 8.5x - 10
Step-by-step explanation:
I think it is substracting because it's how much remains, if its wrong it could either be 10x - 8.5 or 8.5x + 10
What is the sum of 3 of the interior angles of a regular pentagon?
5 stars and like
Answers
Answer: 540°.
Step-by-step explanation:
by
PLEASE PLEASE HELP THIS IS DUE SOONNNN

Answers
Answer:
The height of the tabletop is 75.6 centimeters. Just take 6426 and divide it by 85 and you get 75.6.
Step-by-step explanation:
hope this helped.
Which system of linear inequalities has the point (3, -2) in its solution set?
y < -3; y ≤ 2/3x - 4
y > -3; y ≥ 2/3x - 4
y < -3; y ≥ 2/3x - 4
y > -2; y ≤ 2/3x - 4
Answers
The system that has linear inequalities has the point (3, -2) in its solution set is y > -3; y ≥ 2/3x - 4.
We know that
If a ordered pair is a solution of the system of inequalities, then the ordered pair must satisfy both inequalities (makes true both inequalities)
In option B, we have
y > -3 ----> inequality A
y ≥ 2/3x - 4 ----> inequality B
In both inequality, change the values of x and y at the point (3, -2) and then compare the outcomes.
Inequality A
y > -3 ----> is true
Inequality B
y ≥ 2/3x - 4 ----> is true
Therefore
The ordered pair is a solution of the system B
As a result, the point (3, -2) in the solution set of the system with linear inequalities is y > -3; y 2/3x - 4.
To learn more about linear inequalities click here:
brainly.com/question/11897796
#SPJ4
An Olympic-size swimming pool holds approximately 6×105 gallons of water. The capacity of this swimming pool is between which interval?
Answers
The capacity of this swimming pool is between B. 500 gallons to 1,000 gallons.
What is the capacity?Capacity refers to the product of the length, width, and height of a three-dimensional object or space.
The capacity of an object means the same as its volume.
Olympic-size swimming pools have the following standard dimensions:
Length = 50 m
Width = 25 m
Height = 2 m
Capacity of an Olympic swimming pool = 2,500 m³ (50 x 25 x 2)
= 660,000 gallons (2,500 x 1,000 ÷ 3.785)
An interval estimate shows the lower and upper limits.
6 x 105 gallons = 630 gallons
Thus, the capacity of the swimming pool is Option B.
Learn more about volume or capacity at https://brainly.com/question/463363
#SPJ1
Question Completion with Answer Options:A. 100 gallons to 500 gallons
B. 500 gallons to 1,000 gallons
C. 1,000 gallons to 1,500 gallons
D. 1,500 gallons to 2,000 gallons
27. 10) Three and one half dozen equals? *
I
Answers
Answer:
I think it is 42.
Because one dozen is equal to 12, and we have 3 dozens, which is equal to 36, then add a half dozen, which is 6, then the total answer will be:
12+12+12+6= 42
I hope this helps.
Answer:
42
Step-by-step explanation:
3.5 dozen is 42
Dozen is 12. 12*3.5= 42
Name 2 alternate exterior angles
Answers
Answer:
When two lines are crossed by another line (called the Transversal): Alternate Exterior Angles are a pair of angles on the outer side of each of those two lines but on opposite sides of the transversal. In this example, these are two pairs of Alternate Exterior Angles: a and h.
Step-by-step explanation:
A tourist from Britain wants to exchange her British pounds for US dollar. She has 25 British pounds. How many US dollars would she get in exchange for her British pound if 1 British pound can be exchanged for 1.53 US dollars?
Answers
Answer:
$38.25 US dollars.
Step-by-step explanation:
25 / 1 = 25
To find the number of US dollars that can be exchanged for 25 British pounds, multiply 1.53 by 25 to get $38.25 US dollars.
Hope this helps!
if there is something wrong, just let me know.
My child is in 5th grade ..Please assist with this question..
If 12 boys take 3 days to paint a room,how long will it take 9 boys to complete the same job?
Answers
Please separate your final answer.

Answers
One second later, the distance between the two stones will change in a speed of 6.86 m/s
What is distance ?Distance can be defined as the length of change of position. When an object change from one position to another, the length between the points or position is known as distance.
If a dropped stone has a distance d = 4.9t²
Let us assumed that the time taken = 3 seconds
The distance d = 4.9 × 3² = 44.1 m
If another stone is dropped one second later, then the time t = 4 s
The distance = 4.9 × 4² = 78.4 m
One second later, the time = 5 seconds
The speed of change in distance = ( 78.4 - 44.1 )/ 5
The speed of change in distance = 34.3 / 5
The speed of change in distance = 6.86 m/s
Therefore, one second later, the distance between the two stones will change in 6.86 m/s
Learn more about Speed here: https://brainly.com/question/26046491
#SPJ1
There are 18 men on 2 baseball teams. 2/3 of them brought their sons to watch them play. How many brought their son?
Answers
reasoning:
2/3 of 18 is 12
Do the segments connecting points A, B, and C form a right triangle? Show work that leads to your answer. Round to the nearest tenths place if necessary.
A= -2,2
B=6,2
C=0,6
Answers
Step-by-step explanation:
we need to calculate the distances between the points as the side lengths of the triangle.
these side lengths must satisfy the Pythagoras principle :
c² = a² + b²
with c being the Hypotenuse (side opposite of the 90° angle) and the longest of the 3 sides, a and b being the legs.
the distance between 2 points is again calculated via Pythagoras, as the coordinate differences (= the legs) with the distance as Hypotenuse create right-angled triangles.
this is then caked the distance formula, but it is all Pythagoras again.
AB² = (xB - xA)² + (yB - yA)² = (6 - -2)² + (2 - 2)² =
= 8² + 0² = 8²
AB = 8
AC² = (0 - -2)² + (6 - 2)² = 2² + 4² = 4 + 16 = 20
AC = sqrt(20)
BC² = (0 - 6)² + (6 - 2)² = (-6)² + 4² = 36 + 16 = 52
BC = sqrt(52)
as sqrt(20) is a little bit more than 4, and sqrt(52) is a little bit more than 7, 8 is the longest side and Hypotenuse.
if this is a right-angled triangle, then
8² = sqrt(20)² + sqrt(52)²
must be true.
but
64 = 20 + 52 = 72
is wrong.
so, the segments do not form a right-angled triangle.
Select all that apply
A useful method to interpret the estimated coefficient is to highlight the changing impact of x on p. For instance, given x = 10, we compute the predicted probability as 0.4256. For x = 11, the predicted probability is pˆ=0.4700. Therefore, as x increases by one unit from 10 to 11, the predicted probability changes. Which of the following is true? Select all that apply!
The predicted probability increases by 0.0444 if x increases from 20 to 21
The predicted probability changes by 0.0444 but it could increase or decrease
The predicted probability increases by 0.0444
The increase in pˆ will not be the same if x increases from 20 to 21
Answers
As x increases by one unit from 10 to 11, the predicted probability changes. The predicted probability increases by 0.0444 if x increases from 10 to 11. The correct option is C.
The estimated coefficient in this scenario indicates the change in the predicted log odds of the response variable for a one-unit increase in the predictor variable, holding all other variables constant. In other words, we can interpret it as the changing impact of x on the log odds of the response variable.
To compute the predicted probability, we need to apply the inverse of the logistic function to the linear predictor (i.e., the estimated log odds). Then, we can compare the predicted probabilities for different values of x to see how the change in x affects the response.
The statement "the predicted probability changes by 0.0444 but it could increase or decrease" is incorrect because we know from the given information that the predicted probability increases as x increases from 10 to 11.
The statement "the increase in pˆ will not be the same if x increases from 20 to 21" is also incorrect because we are not given any information about the estimated coefficient or predicted probability for x = 20 or x = 21, so we cannot make any conclusions about the change in pˆ for that interval.
To learn more about probability click on,
https://brainly.com/question/24239758
#SPJ4
Complete question is:
Select all that apply
A useful method to interpret the estimated coefficient is to highlight the changing impact of x on p. For instance, given x = 10, we compute the predicted probability as 0.4256. For x = 11, the predicted probability is pˆ=0.4700. Therefore, as x increases by one unit from 10 to 11, the predicted probability changes. Which of the following is true?
A. The predicted probability increases by 0.0444 if x increases from 20 to 21
B. The predicted probability changes by 0.0444 but it could increase or decrease
C. The predicted probability increases by 0.0444 if x increases from 10 to 11.
D. The increase in pˆ will not be the same if x increases from 20 to 21
need help with this question , thanks

