Answers
The triangles are similar triangles. Then the value of the variable 'x' will be 6.
What is the triangle?The polygonal shape of a triangle has a number of sides and three independent variables. Angles in the triangle add up to 180 °.
The ratio of the matching sides will remain constant if two triangles are comparable to one another.
Similar triangles are shown below.
We know that the ratio of the corresponding sides of similar triangles remains constant. Then the equation is given as,
(6x - 1) / 15 = 14 / 6
Simplify the equation, then we have
(6x - 1) / 15 = 14 / 6
(6x - 1) / 5 = 7
6x - 1 = 35
6x = 36
x = 6
The triangles are comparable triangles. Then, at that point, the worth of the variable 'x' will be 6.
More about the triangle link is given below.
https://brainly.com/question/25813512
#SPJ1
Related Questions
25-4x=15-13x+10-x
Find the value of X pls and ty
Answers
Answer:
x=0
Step-by-step explanation:
use a website called 'tiger-algebra.com'
i hope this helped!
The height of the tank is 11 m and the radius of the tank is 5 m. the height of the water is 6 m and the radius of the water is 3 m. how much more water in cubic meters could you fit in the tank?
Answers
Answer:
221 cubic metre.
Step-by-step explanation:
Volume of water in tank (v) = π × {3}^{2} × 6
= 54π cubic metre
Volume of tank (v') = π × {5}^{2} × 11
= 275π cubic metre
More Water that can be fit in the tank = v' - v
=275π - 54π
= 221π cubic metre.
ANS.
14Y - 7y = 35. solve for y
Answers
Answer:
y = 5
Step-by-step explanation:
\(14y-7y=35\\7y=35\\y=5\)
14 minus 7 is 7
7Y is equal to 35
divide both sides by 7 is equal to 5
A gas station sells regular gas for $2.30 per gallon and premium gas for $3.00 a gallon. At the end of a business day 320 gallons of gas had been sold, and receipts totaled $799. How many gallons of each type of gas had been sold
Answers
Answer:
90 gallons premium gas
230 gallons regular gas
Step-by-step explanation:
We can use the given information to form a system of equations.
First, let's set the variables:
Regular gas: r
Premium gas: p
Throughout the entire day, they sold 320 gallons of r and p combined.
r+p=320
Now, regular gas sells for 2.30 per gallon, which can be written as 2.30r
premium can be shown similarly as 3.00p. After all the gallons they sold, they got 799 in total.
2.30r + 3.00p = 799
As a system of equations, it can be written like this...
r+p=320
2.30r + 3.00p = 799
Now solve. (I won't explain much of the steps here but I'll show it. Comment questions if you have any, and I'll try to answer them.)
r=320-p
2.30r + 3.00p = 799
2.30(320-p)+3.00p=799
736+0.7p=799
0.7p=63
p=90 gallons of premium gas
Now we can solve for regular by just plugging in 90 gallons premium into the top equation.
r+p=320
r+90=320
r=230 gallons of regular gas
check work.
230(2.30)+90.0(3.00)=799
529+270=799
799=799
slope of 3,-4 and 5,8
Answers
Answer:
Slope = 6
Step-by-step explanation:
Use the slope formula:
\(m=\frac{y_1-y_2}{x_1-x_2}\\m=\frac{-4-8}{3-5}\\m=\frac{-12}{-2}\\m=6\)
Answer:
6
Step-by-step explanation:
(3,-4) and (5,8)
To find the slope of the line, we use the slope formula: (y₂ - y₁) / (x₂ - x₁)
Plug in these values:
(8 - (-4)) / (5 - 3)
Simplify the parentheses.
= (8 + 4) / (5 - 3)
= (12) / (2)
Simplify the fraction.
12/2
= 6
This is your slope.
Hope this helps!
what is mean by migration
who will give me brainlest then I am follow you
Answers
Step-by-step explanation:
Movement from one place to another
Find the equation of the parabola with the following properties. Express your answer in standard form.
Focus at (4, -3)
Directrix is the line x = 0
Answers
The standard form of the equation of the parabola with a focus of (4, -3), and a directrix of x = 0 is; (y + 3)² = 8·(x - 2)
How can the equation of a parabola be found from the focus and the directrix?The equation of a parabola with a focus (4, -3) and a directrix of x = 0, can be found using the definition of the curve of a parabola, which is a curve that describes the location of a point that is equidistant from the focus and the directrix.
Let (x, y) represent the coordinate of the point, therefore;
The distance of the point from the point to the focus is therefore;
Distance = √((x - 4)² + (y + 3)²)
The distance from between the point and the directrix = |x|
According to the definition of the locus of a parabola, therefore;
√((x - 4)² + (y + 3)²) = |x|
(x - 4)² + (y + 3)² = x²
x² + y² - 8·x + 6·y + 25 = x²
x² - x² + y² - 8·x + 6·y + 25 = 0
y² - 8·x + 6·y + 25 = 0
y² + 6·y + 25 = 8·x
However, we get; Directrix, x = h - p
focus = (h + p, k)
Therefore;
h + p = 4
k = -3
h - p = 0
2·h = 4 + 0 = 4
h = 4/2 = 2
h = 2
p = 4 - 2 = 2
p = 2
The equation of a parabola is; (y - k)² = 4·p·(x - h)
The equation of the parabola is; (y - (-3))² = 4 × 2 × (x - 2)
The standard form of the equation is therefore;
(y + 3)² = 8·(x - 2)
Learn more on the equation of a parabola here: https://brainly.com/question/23952969
#SPJ1
I need help pleas I need it please please please free 50 points

Answers
Answer:
answer is 0
Step-by-step explanation:
Answer:
its zero
Step-by-step explanation:
28 divided by 4 is 7
7 to the power of 2 is 49
49 divided by 7 is 7
7-7 is 0
For the given functions, state the domain using an appropriate notation and evaluate f(2)

Answers
Given the equation:
\(f(x)=\log _4x\)the given equation is for logarithm function with a base of 4
The domain will be all real numbers of x
So,
\(Domain=(0,\infty)\)We will find the value of f(2)
So, substitute with x = 2 and solve
so,
\(\begin{gathered} f(2)=\log _42 \\ 2=\sqrt[]{4}=4^{\frac{1}{2}} \\ \\ f(2)=\log _42=\log _44^{\frac{1}{2}}=\frac{1}{2}\cdot\log _44=\frac{1}{2}\cdot1=\frac{1}{2} \end{gathered}\)So, the answer will be:
\(f(2)=\frac{1}{2}\)22
Question 6 Multiple Choice Worth 1 points)
(04.02 LC)
For the following system, if you isolated x in the second equation to use the substitution method, what expression would you substitute into the first equation?
3x + y = 8
-x - 2y = -10
O-2y + 10
O 2y + 10
O 2y - 10
O-2y - 10
Answers
Answer:
-2y + 10
Step-by-step explanation:
Substitution method:
On the second equation of the system, we have to find x as a function of y.
-x - 2y = -10
We have to find x as a function of y, so:
\(-x = -10 + 2y\)
Multiplying both sides of the equality by -1:
\(x = -2y + 10\)
So -2y + 10 is the answer to this question.
(x-3)(x-4)/(x-4)(x-4)
Answers
Answer:
(x-3) (x-4)/(x-4)
x(x-4)-3 (x-4)/(x-4)
this is the answer!
if you have any problem tell me I will help you
Answer:
the answer is on the picture

Which is the algebraic representation for a rotation 180° clockwise?

Answers
answer: I guess it is (-x,-y)
Please match the following 3 terms to their definitions.

Answers
Answer:
See attached
Step-by-step explanation:
Refer to picture

Question: 18 of 19
Lesson 18
Find the component form of the following vectors. Round your answers to the tenth.
Magnitude of v = 50, direction angle 0 = 50°
Choice 'A' OV
Choice 'B'O V
Choice 'C'OV
Choice 'D' OV
(38.3, 32.1)
(33.8, 31.2)
(32.1, 38.3)
(31.2, 33.8)
4

Answers
The component form of the following vectors is Option A. V = (38.3, 32.1).
To find the component form of a vector given its magnitude and direction angle, we can use trigonometry.
The component form of a vector in two dimensions is represented as (x, y), where x is the horizontal component and y is the vertical component.
In this case, the magnitude of the vector is given as 50, and the direction angle θ is 50°. We can use this information to calculate the horizontal and vertical components.
The horizontal component (x) can be found using the formula x = magnitude * cos(θ), and the vertical component (y) can be found using y = magnitude * sin(θ).
Let's calculate the components:
x = 50 * cos(50°) ≈ 38.3
y = 50 * sin(50°) ≈ 32.1
Rounding the answers to the nearest tenth, we get the component form of the vector V as (38.3, 32.1).
Therefore, the correct answer is A. V = (38.3, 32.1).
Know more about the vectors here:
https://brainly.com/question/30854499
#SPJ8
The question is incomplete. Find the full content below:
Find the component form of the following vectors. Round your answers to the tenth.
Magnitude of v = 50, direction angle θ = 50°
A. V = (38.3, 32.1)
B. V = (33.8, 31.2)
C. V = (32.1, 38.3)
D. V = (31.2, 33.8)
Type the correct answer in the box.
Fill in the missing term in the equation.
(1 + 2)(2+1) + blank
= 5(2+i)
Answers
(1 + 2)(2 + 1) + blank
= 3(3) + blank
= 9 + blank
Expanding the right side of the equation:
5(2 + i)
= 10 + 5i
Since the left side of the equation (9 + blank) is equal to the right side (10 + 5i), we can deduce that the missing term should be equal to 1i.
Therefore, the missing term in the equation is "1i".
)The mean voltage of a battery is 15 and S.D 0.2.Find the probability that four such batteries connected in series will have combined voltage of 60.8 or more volts
Answers
The probability that four batteries connected in series will have a combined voltage of 60.8 or more volts is approximately 0.0228 or 2.28%.
To find the probability that four batteries connected in series will have a combined voltage of 60.8 or more volts, we need to use the concept of the Central Limit Theorem.
In this case, we know that the mean voltage of a single battery is 15 volts and the standard deviation is 0.2 volts. When batteries are connected in series, their voltages add up.
The combined voltage of four batteries connected in series is the sum of their individual voltages. The mean of the combined voltage will be 4 times the mean of a single battery, which is 4 * 15 = 60 volts.
The standard deviation of the combined voltage will be the square root of the sum of the variances of the individual batteries. Since the batteries are connected in series, the variance of the combined voltage will be 4 times the variance of a single battery, which is 4 * (0.2)^2 = 0.16.
Now, we need to calculate the probability that the combined voltage of four batteries is 60.8 or more volts. We can use a standard normal distribution to calculate this probability.
First, we need to standardize the value of 60.8 using the formula:
Z = (X - μ) / σ
Where X is the value we want to standardize, μ is the mean, and σ is the standard deviation.
In this case, the standardized value is:
Z = (60.8 - 60) / sqrt(0.16)
Z = 0.8 / 0.4
Z = 2
Next, we can use a standard normal distribution table or calculator to find the probability associated with a Z-score of 2. The probability of obtaining a Z-score of 2 or more is approximately 0.0228.
Therefore, the probability that four batteries connected in series will have a combined voltage of 60.8 or more volts is approximately 0.0228 or 2.28%.
Learn more about probability here:
https://brainly.com/question/23417919
#SPJ8
Example 1: Alena knows that her morning cup of coffee is a discretionary expense. She pays $2.75 for a 9-oz cup and was wondering if that is a typical price. On Monday, she asked 6 of her friends what they paid for a 9 oz cup of coffee. Their costs per cup were $2.85, $2.15, $1.95, $3.00, $2.05 and $2.40 SIGMA NOTATION Example 2: Use the information on page 6 of your text to examine the list of coffee prices in Example 1 (above). Find the mean using sigma notation.
Answers
The mean using sigma notation is $2.4
How to find the mean using sigma notation?The list of costs per cup are given as:
$2.85, $2.15, $1.95, $3.00, $2.05 and $2.40
The mean using sigma notation is calculated as:
\(\bar x = \frac{\sum x}{n}\)
This gives
\(\bar x\) = ($2.85 + $2.15 + $1.95 + $3.00 + $2.05 + $2.40)/6
Evaluate the sum
\(\bar x\) = $14.4/6
Evaluate the quotient
\(\bar x\) = $2.4
Hence, the mean using sigma notation is $2.4
Read more about mean at:
https://brainly.com/question/14532771
#SPJ1
12 is 58% of what number?
Also can you explain how to solve these problems?
Answers
Answer:
20.68976
Step-by-step explanation:
Convert the percentage into decimal :
58% = 0.58
0.58 × x = 12
Divide both sides by 0.58 :
x = 12÷0.58
x = 20.689655...
x = 20.68976
So the method to these types of question is to make the question into an equation by converting the percentage into a decimal, rearrange to make the unknown number the subject and solve .
Hope you understood and have a good day
PLSSS HElpppp!! DUE TODAYYY⛔️
Some children measured the lengths of their feet. The lengths are given in the line plot. What is the difference in length between the shortest and longest foot?

Answers
Answer:
Step-by-step explanation:
A cylinder has a circular base with a radius of 3units and a height of 7 units. What is the volume of the cylinder in cubic units?
Answers
The volume of the cylinder is the extension of the base area throughout its length thus the volume of the given cylinder will be 198.
What is volume?Volume is the scalar quantity of any object that specified occupied space in 3D.
For example, the space in our room is referred to as volume.
The volume of the cuboid = length × height × width.
As per the given cylinder,
The radius of the base of the cylinder = 3
Height = 7
Base area = π(radius)²
Base area = π(3)²
Base area = 9π
The volume of the cylinder = Base area × Height
Volume = 9π × 7 = 198.
Hence "The volume of the cylinder is the extension of the base area throughout its length thus the volume of the given cylinder will be 198".
To learn more about volume,
https://brainly.com/question/1578538
#SPJ1
What is 2+2 (Hint is not 4)
Answers
Answer:
5...?
Step-by-step explanation:
Answer:
7
Step-by-step explanation:
The answer is 7 because a 2 reversed looks like a 5 and 2+5=7
F (X) = x² - 2x and 6(x) = 3x+1
A) Find F(g(-4))
B) Find F(g(x)) simply
C) find g^-1 (x)
Answers
Answer: See bolded below
Step-by-step explanation:
With the given f(x) and g(x) given, we can directly plug them in to solve. The inverse is to replace the y with x and x with y, then solve for y.
A. f(g(-4))=143
g(-4)=3(-4)+1
g(-4)=-12+1
g(-4)=-11
With g(-4), we plug that into f(x) to find f(g(-4)).
f(-11)=(-11)²-2(-11)
f(-11)=121+22
f(-11)=143
------------------------------------------------------------------------------------
B. 9x²-1
(3x+1)²-2(3x+1)
(9x²+6x+1)-6x-2
9x²-1
------------------------------------------------------------------------------------
C. g⁻¹(x)=(x-1)/3
x=3y+1
x-1=3y
(x-1)/3=y
Am nevoie de raspuns la acest exercitiu.

Answers
For the following vectors, (a) find the dot product v•w ; (b) find the angle between v and w , (c) state whether the vectors are parallel, octagonal, or neither. V=-3i-4j, w=6i+8j
A- v•w
B-the angle between v and w is theta ^•?
C- the vectors v and w are?
Answers
B) The angle between vectors v and w can be found using the formula: cos(theta) = (v • w) / (||v|| ||w||), where ||v|| and ||w|| are the magnitudes of vectors v and w respectively.
First, we need to find ||v|| and ||w||:
||v|| = sqrt((-3)^2 + (-4)^2) = 5
||w|| = sqrt((6)^2 + (8)^2) = 10
Now, we can substitute in the values to get:
cos(theta) = (-50) / (5 * 10) = -1
theta = arccos(-1) = pi radians or 180 degrees.
Therefore, the angle between vectors v and w is 180 degrees.
C) Two vectors are parallel if their directions are the same, which can be determined by comparing their unit vectors.
The unit vector of v is:
v_hat = v / ||v|| = (-3/5)i + (-4/5)j
The unit vector of w is:
w_hat = w / ||w|| = (6/10)i + (8/10)j = (3/5)i + (4/5)j
We can see that the unit vectors are in opposite directions, which means that the vectors are anti-parallel or opposite. Therefore, the vectors v and w are neither parallel nor orthogonal.
There are 350 books at most in 2 shelves, how many books at most in 5 shelves?
Answers
Convert 2 days into months. Round your answer to the nearest hundredth.
Answers
Answer:
0.0657534
Step-by-step explanation:
divide 2 by 30.417
\( 3 {x}^{2} - 15x = 15\)
Answers
\(3x^2-15x= 15\\\\x^2 -5x = 5\\\\x^2-5x-5=0\\\\\Delta = 25+20\\\\\Delta = 45\\\\\\x = \dfrac{5\pm \sqrt{\Delta}}{2}\\\\\\x = \dfrac{5\pm \sqrt{45}}{2}\\\\\\x = \dfrac{5\pm 3\sqrt{5}}{2}\\\\\\\)
Find the equation with vertex(-2,5) and focus(1,5)
Answers
Answer:
\((y-5)^2=12(x+2)\)
Step-by-step explanation:
Since the focus point is directly right of the vertex, the axis of symmetry will be horizontal, which means that we use the equation \((y-k)^2=4p(x-h)\) where \((h,k)\) is the vertex and \((h+p,k)\) is the focus point.
Since we know our vertex to be \((h,k)\rightarrow(-2,5)\) and our focus point to be \((h+p,k)\rightarrow(1,5)\), the distance from the vertex to the focus point is \(p=3\).
Hence, the equation is:
\((y-5)^2=4(3)(x-(-2))\\\\(y-5)^2=12(x+2)\)

Find M Please help!!!! Last question worth 10 points!
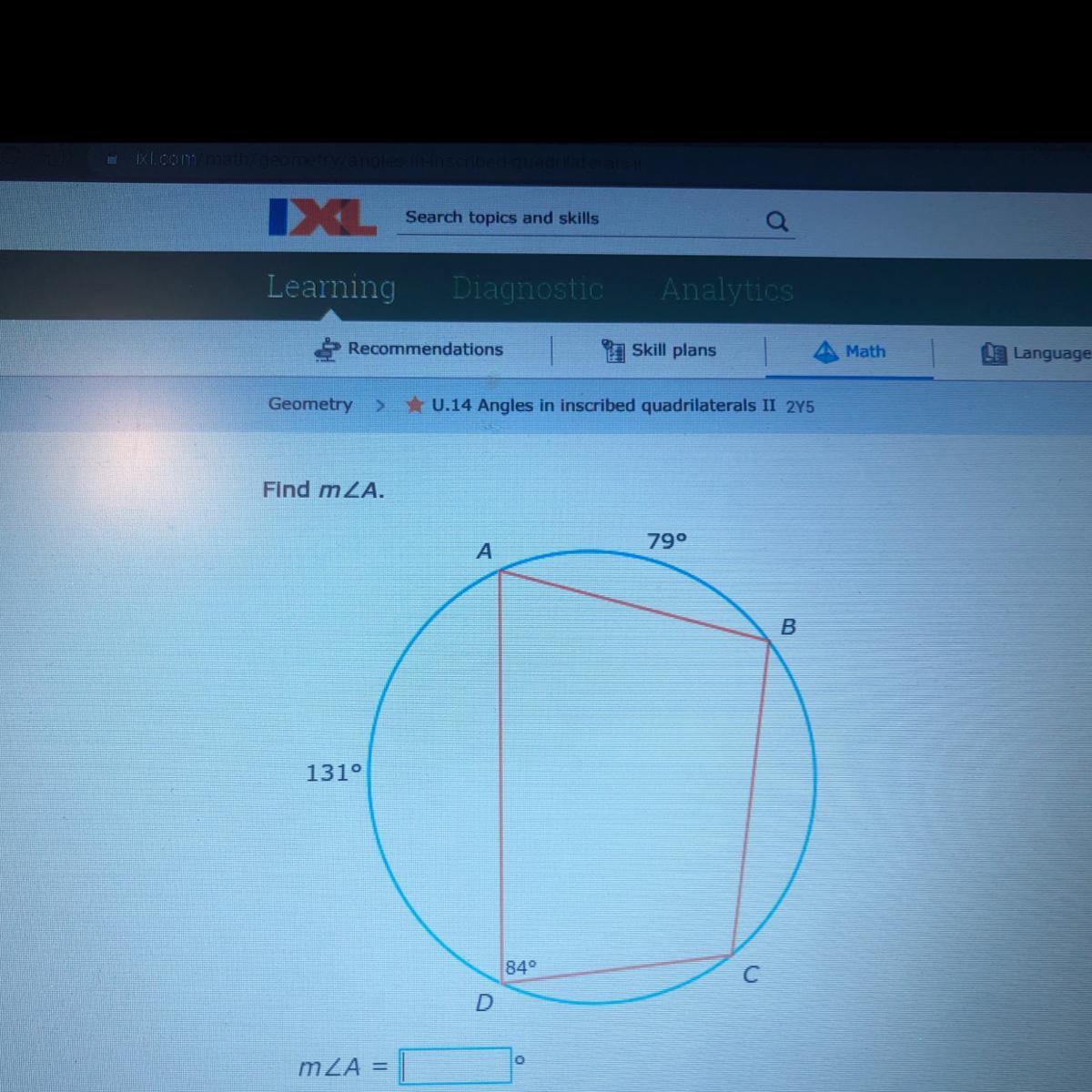
Answers
Answer:
<A = 75degrees
Step-by-step explanation:
From the triangle given;
arcDA + arc AD + arcBD = 360 degrees
131 + 79 + arcBD = 360
210 + arcBD = 360
arcBD = 360 -210
arcBD = 150 degrees
Since the angle at the vertex <A is half that at the arc BD, hence;
<A = 1/2 arcBD
<A = 1/2 * 150
<A = 75degrees
Hence the measure of angle A s 75degrees
Rolling a 2 on a number cube is
1. likely
2. unlikely
3. as likely as not (50/50)
4. impossible
5. certain

Answers
Answer:
2. unlikely
Step-by-step explanation:
The probability of rolling a 2 is 1/6, 0r 0.1666... .
Probabilities and their meanings:
0 - impossible
between 0 and 0.5 - from unlikely to almost as likely as not
0.5 - as likely as not
between 0.5 and 1 - from as likely as not to almost certain
1 - certain
This probability is 0.1666... which is in the category from 0 to 0.5. It is closer to 0 than to 0.5, so although it is not impossible, it is unlikely.
Answer: 2. unlikely
