Answers
Answer:
∠ S = 58° , ∠ T = 64° , ∠ Q = 58°
Step-by-step explanation:
the sum of the 3 angles in Δ DQS = 180° , that is
∠ Q + ∠ 1 + 90° = 180°
∠ Q + 32° + 90° = 180°
∠ Q + 122° = 180° ( subtract 122° from both sides )
∠ Q = 58°
given ST = TQ , then Δ STQ is isosceles with base angles congruent, that is
∠ S = ∠ Q = 58°
the sum of the 3 angles in Δ STQ = 180° , that is
∠ T + ∠ S + ∠ Q = 180°
∠ T + 58° + 58° = 180°
∠ T + 116° = 180° ( subtract 116° from both sides )
∠ T = 64°
Related Questions
find the zeros of the function. State the multiplicity of multiple zeros.
y=7x^3-7x select the correct choice below and if necessary fill in the boxes within your choice.
1. The numbers _ are zeros of multiplicity 3
2. The numbers _ are zeros of multiplicity 2
3. The numbers _ are zeros of multiplicity 1
4. The numbers _ are zeros of multiplicity 1 and the numbers _ are zeros of multiplicity 2.
(picture added if needed :))

Answers
The numbers 0, 1, and -1 are zeros of multiplicity 1.
What is quadratic equation?
it's a second-degree quadratic equation which is an algebraic equation in x. Ax2 + bx + c = 0, where a and b are the coefficients, x is the variable, and c is the constant term, is the quadratic equation in its standard form. A non-zero term (a 0) for the coefficient of x2 is a prerequisite for an equation to be a quadratic equation. The x2 term is written first, then the x term, and finally the constant term is written when constructing a quadratic equation in standard form. In most cases, the numerical values of letters a, b, and c are expressed as integral values rather than fractions or decimals.
To find the zeros of the function \(y=7x^3-7x\), we can set y equal to zero and solve for x:
\(7x^3 - 7x = 0\)
Factor out 7x:
\(7x(x^2 - 1) = 0\)
Factor the quadratic expression:
7x(x - 1)(x + 1) = 0
The zeros of the function are the values of x that make y equal to zero. From the factored expression, we see that the zeros are:
x = 0 (with multiplicity 1)
x = 1 (with multiplicity 1)
x = -1 (with multiplicity 1)
Therefore, the correct choice is: The numbers 0, 1, and -1 are zeros of multiplicity 1.
Learn more about quadratic equation , by the following link.
https://brainly.com/question/1214333
#SPJ1
You are installing a rectangular pool in your backyard. The pool measures 24 feet by 16 feet. You also would like to build a concrete walkway around the pool. You have allocated 560 ft? of your backyard for both the pool and the walkway around it. How wide should you make the walkway?
Answers
Answer:
The walkway should be 2ft wide.
Step-by-step explanation:
Let x be the width of the walkway surrounding the pool.
The area including the pool is 560ft².
Let's solve for the value of x.
The length plus twice the width of the pool is multiplied by the width plus twice the width of the pool. This makes up the whole area.
A = lw
560 = (24 + 2x)(16 + 2x)
560 = 384 + 48x + 32x + 4x²
4x² + 80x + 384 - 560 = 0
4x² + 80x - 176 = 0
Divide the whole equation by 4
x² + 20x - 44 = 0
(x + 22)(x -2) = 0
x = -22; x = 2
Since we are dealing with dimensions, take the one with the positive value.
x = 2ft
Let's check
560ft² = (24ft + 2x)(16ft + 2x)
560ft² = (24ft + 2(2ft)) (16ft + 2(2ft))
560ft² = (24ft + 4ft)(16ft + 4ft)
560ft² = (28ft)(20ft)
560ft² = 560ft² ✔

Final question no more lives
who ever gives me correct answer will get brainliest

Answers
The time take to fill the pool will be 494 hours.
How to calculate the TimeInlet pipe fills in 38 hours = 1 pool
Inlet pipe fills in 1 hours = 1/38
Drain pipe empty in 39 hours = 1 pool
Drain pipe empty in 1 hour = 1/39
If both pipes are opened together then in pool fills in 1 hour = 1/38 - 1/39
= 1/1482
Therefore, 1/1482 fills in 1 hour.
. Therefore, 1/3 will be:
= 1/3 × 1482
= 494 hours.
Learn more about fractions on:
https://brainly.com/question/78672
#SPJ1
A can factory requires 2 sheets of metal to make 36 cans and 10 sheets of metal to make 180 cans. The proportionality constant between the number of cans made and the number of sheets of metal used is 36 18 288 5
Answers
Answer:From the statement above, we can say that there is a direct relationship between the number of sheets used to the number of cans that can be made. That is, # of sheets is directly proportional to # of cans. We make an equation as follows:
let y = # of sheets
x = # of cans
y = kx where k is the proportionality constant
Assuming linear relationship of the two, we can use either data point as follows:
y = kx
2 = k(36)
k = 1/18
Therefore, the proportionality constant is 1/18.
Step-by-step explanation:
Your pool is 80 ft long by 40 ft wide and the depth is 3ft to 8ft what is the pool volume?
Answers
Answer:
Since there are 7.5 gallons in each cubic foot, multiply the cubic feet of the pool by 7.5 to arrive at the volume of the. 3.14 x 25 ft x 3 ft x 7.5 = 1766.25 gallons
Step-by-step explanation:
Your friend gives you the right triangle above and to the left and says. "Bisecting an angle is really easy. Take triangle ABC. If I wanted to bisect
(a) Convince your friend that they are wrong. Use what you know about trigonometry to explain why CAD and DAB are not congruent.
(b)locate the point E on that lies on the angle bisector of CAB.How far is point E from point B?Show all your work

Answers
I) The angles are not equal then the two triangles are not Congruent.
ii) The point E is 1.5 from point B.
What is Bisector?
A line that divides the line into two distinct or equal segments is referred to as a "bisector." It is applied to angles and line segments.
A ray that divides an angle into two equal pieces is known as an angle bisector or the bisector of an angle.
Given:
As, <CAB = 19.4 and <DAB = 33.7
So, CAD and DAB are not congruent.
ii) The point E should be located 1.5 away from point B.
Learn more about Bisector here:
https://brainly.com/question/28663444
#SPJ1
Bob and Sarah invest $7000 eachfor 5 years.Bob invests his money at3.5%, simple interest andSarah invests her money at 3.5% interestcompounded annually.How much more interest will Sarah have earned thanBob at the end of the 5 years?A) $1225.80O $709080D) Sa8.80B) $1313.80
Answers
Bob investment
\(\begin{gathered} I=\frac{prt}{100} \\ I=\frac{7000\times3.5\times5}{100} \\ I=\frac{122500}{100} \\ I=\text{ \$}1225 \end{gathered}\)Sarah's investment
\(\begin{gathered} A=P(1+\frac{r}{n})^{nt} \\ A=7000(1+\frac{0.035}{1})^5 \\ A=7000\times1.18768630565 \\ A=8313.80413953 \\ I=8313.80413953-7000 \\ I=\text{ \$}1313.80413953 \\ \end{gathered}\)Difference(sarah interest - Bob interest) = 1313.80413953 - 1225 = 88.8041395281 = $88.80
Therefore, Sarah have $88.80 interest more than Bob.
Can someone solve this please

Answers
Answer:
i guess 3/8
because it is third part of the whole 8 part .
i hope you get it!?
using the cross-multiplication rule

I am so confused right now. will give brainlest to anyone how can solve this chicken scratch lol
1. Write an equation representing this hanger
2. find the value (or "weight) of one circle (w).
3. Explain how you found the value of one circle (w)
I really have no idea what any of this is

Answers
Answer:
1. 25÷4w
2. w=6.25
3.I divided 25 by 4 to find w
Step-by-step explanation:
I need help with this PLEASE!!!

Answers
Answer:
See the image for marked congruences.
1. JM ≅ LM | Given
2. △JML is isosceles | definition of isosceles
3. ∠MJL ≅ ∠MLJ | isosceles triangle theorem
4. m∠MJL = m∠MLJ | definition of ≅
5. JK ≅ LK | Given
6. △JKL is isosceles | definition of isosceles
7. m∠KJL = m∠KLJ | isosceles triangle theorem
8. m∠MJL + m∠KJM = m∠KJL | adjacent angle theorem
9. m∠MLJ + m∠KMJ = m∠KLJ | adjacent angle theorem
10. m∠MJL + m∠KJM = m∠MLJ + m∠KLM | transitive property of =
11. m∠MJL + m∠KJM = m∠MJL + m∠KLM | substitution
12. m∠KJM = m∠KMJ | subtraction
13. ∠KJM ≅ ∠KLM | definition of ≅
14. △KJM ≅ △KLM | SAS theorem
15. ∠JKM ≅ ∠LKM | CPCTC
16. KM bisects ∠JKL | definition of bisector

Janet is 33.3% finished with
her math homework. If she
has 24 questions, how many
does she have left to finish?
Answers
Write an expression to represent the product of 6 and the square of a number plus 15. In your expression what is the value of the coefficient? A. 1 B. 6 C. 15 D. 2
Answers
Answer:
B) 6
Step-by-step explanation:
Let the number be x
Product of 6 and square of number plue 15 : (6x²) + 15
Coefficient of x² = 6
Sheri saves nickels and dimes in a coin purse for her daughter. The total value of the coins in the purse is $0.70. The number of nickels is two less than six times the number of dimes.
How many nickels and how many dimes are in the coin purse?
Answers
Answer:
Step-by-step explanation:
Let's start by assigning variables to represent the unknowns in the problem. We can use "n" to represent the number of nickels and "d" to represent the number of dimes.
From the problem statement, we know that the total value of the coins in the purse is $0.70. We can write an equation to represent this information:
0.05n + 0.10d = 0.70
We also know that the number of nickels is two less than six times the number of dimes. We can write an equation to represent this information:
n = 6d - 2
Now we can substitute the expression for "n" into the first equation:
0.05(6d - 2) + 0.10d = 0.70
Simplifying the left side of the equation, we get:
0.30d - 0.10 + 0.10d = 0.70
Combining like terms, we get:
0.40d = 0.80
Dividing both sides by 0.40, we get:
d = 2
So there are 2 dimes in the coin purse. Now we can use the second equation to find the number of nickels:
n = 6d - 2 = 6(2) - 2 = 10
So there are 10 nickels in the coin purse.
Therefore, Sheri has 10 nickels and 2 dimes in the coin purse for her daughter.
What is the total weight of the bags that weighed /8 pound each?
Answers
The total weight of Rice that Mark buys is given as follows:
2.5 pounds.
How to obtain the total weight?The total weight of Rice that Mark buys is obtained applying the proportions in the context of the problem.
The weight of each bag is given as follows:
5/8 pounds = 0.625 pounds.
The number of bags is given as follows:
4 bags.
Hence the total weight of Rice that Mark buys is given as follows:
4 x 0.625 = 2.5 pounds.
More can be learned about proportions at https://brainly.com/question/24372153
#SPJ1

State the name of the property illustrated.
4(-8+5)= - 32 + 20
Answers
The property illustrated in equation 4(-8+5) = -32 + 20 is the Distributive Property.
The Distributive Property states that when a number is multiplied by a sum or difference in parentheses, it can be distributed or multiplied by each term inside the parentheses separately, and then the results can be added or subtracted.
In this case, the number 4 is multiplied by the sum (-8 + 5). By applying the Distributive Property, we distribute the 4 to each term inside the parentheses:
4(-8 + 5) = (4 * -8) + (4 * 5)
This simplifies to:
4(-8 + 5) = -32 + 20
Finally, we can perform the addition:
-32 + 20 = -12
Therefore, the equation demonstrates the application of the Distributive Property.
know more about Distributive Property here:
https://brainly.com/question/2807928
#SPJ8
In a cell phone plan Bao pays a flat rate of $40.50 a month snd $5.00 per gigabyte She wants to keep her bill under $60.00. Write and solve an inequality which can silve the number of gigabytes she can use to stay within her buget.
Answers
We can write the inequality as: 5N + 45 < 60
The solution of the inequality is: N < 3
How to write and solve an inequality?An inequality is a relationship that makes a non-equal comparison between two numbers or other mathematical expressions e.g. 2x > 4
Let N represent the number of gigabytes she can use to stay within her budget.
Bao pays a flat rate of $40.50 a month. That is constant: $45
$5.00 per gigabyte. For N gigabyte, we have: $5 * N = 5N
She wants to keep her bill under $60.00. This means the total is less than 60 (< 60)
Thus, we can write the inequality as:
5N + 45 < 60
We can solve the inequality by making N the subject. That is:
5N + 45 < 60
5N < 60 - 45
5N < 15
N < 15/5
N < 3
This implies Bao must use less than 3 gigabytes to stay within her budget
Learn more about inequality on:
brainly.com/question/25275758
#SPJ1
The dimensions of a rectangular pyramid are shown.
6, feet. 8, feet. 4, feet.
What is the volume of this rectangular pyramid in cubic feet?
Answers
The volume of the rectangular pyramid is 64 cubic feet.
What is a rectangular pyramid?A pyramid with a rectangular base is known as a rectangle pyramid. When viewed from the bottom, this pyramid seems to be a rectangle. As a result, the base has two equal parallel sides.
The apex, which is located at the summit of the pyramid's base, serves as its crown. Right or oblique pyramids can be seen in rectangular shapes. If it is a right rectangular pyramid, the peak will be directly over the base's center; if it is an oblique rectangular pyramid, the apex will be angled away from the base's center.
The volume of a rectangular pyramid is given as:
V = (l)(b)(h) / 3
V = (6)(8)(4) / 3
V = 192 / 3
V = 64 cubic feet.
Hence, the volume of the rectangular pyramid is 64 cubic feet.
Learn more about volume here:
https://brainly.com/question/1578538
#SPJ1
The correct question is:

In a study researchers reported the mean BMI for men 60 and older to be 24.7 with a standard deviation of 3.3 and the mean BMI for women 60 and older to be 23.1 with a standard deviation of 3.7. Using these values as the populations mean and standard deviation for men and women respectively, find the probability that the difference in the mean BMI (men-women) for 45 women and 50 men selected independently and at random will exceed 2.1.
Answers
Answer:
Probability that the difference in the mean BMI (men-women) for 45 women and 50 men selected independently and at random will exceed 2.1 = 0.2451
Step-by-step explanation:
The central limit theorem helps us to obtain the mean and the standard deviation of any sampling distribution.
Given that the sample was obtained from a normal distribution or an approximately normal distribution & it was obtained using random sampling techniques with each variable independent of one another and with each sample with adequate sample size,
Mean of sampling distribution (μₓ) = Population mean (μ)
Standard deviation of the sampling distribution = σₓ = (σ/√N)
where σ = population mean
N = Sample size
For the 45 women
μₓ = μ = 23.1
σₓ = (σ/√N) = (3.7/√45) = 0.552
For the 50 men
μₓ = μ = 24.7
σₓ = (σ/√N) = (3.3/√50) = 0.467
To find the probability that the difference in the mean BMI (men-women) for 45 women and 50 men selected independently and at random will exceed 2.1, we need to combine the distributions.
New distribution = (BMI of men) - (BMI of women) = x = X₁ - X₂
When independent distributions are combined, the combined mean and combined variance are given through the relation
Combined mean = Σ λᵢμᵢ
(summing all of the distributions in the manner that they are combined)
Combined variance = Σ λᵢ²σᵢ²
(summing all of the distributions in the manner that they are combined)
λ₁ = 1, λ₂ = -1
μ₁ = 24.7, μ₂ = 23.1
σ₁ = 0.467, σ₂ = 0.552
Combined mean = (Mean of men) - (Mean of women) = 24.7 - 23.1 = 1.6
Combined Variance = (1²×0.467²) + [(-1)²×(0.552²)] = 0.522793
Combined standard deviation = √0.522793 = 0.723
Probability that the difference in the mean BMI (men-women) for 45 women and 50 men selected independently and at random will exceed 2.1 = P(x > 2.1)
Note that the resulting distribution from the combination of distributions is still a normal distribution since the distributions combined were normal distributions too.
Hence, we first normalize or standardize 2.1
The standardized score for any value is the value minus the mean then divided by the standard deviation.
z = (x - μ)/σ = (2.1 - 1.6)/0.723 = 0.69
To determine the required probability
P(x > 2.1) = P(z > 0.69)
We'll use data from the normal distribution table for these probabilities
P(x > 2.1) = P(z > 0.69) = 1 - P(z ≤ 0.69)
= 1 - 0.7549
= 0.2451
Hope this Helps!!!
A triangle has vertices of (-3,3),(-3,2), and (1,-2). What are the coordinates after dilating from the origin by a scale factor of 1/2?
Answers
Answer:
The coordinates after a dilating the triangle by a factor of 1/2 would be (-1.5, 1.5), (-1.5, 1) and (0.5, -1), respectively.
Step-by-step explanation:
Since we are dilating from the origin of the graph, (0, 0), all we need to do is multiply each vertex by the given scale factor.
19. Describe the graph of a proportional relationship.
Answers
The graph of a proportional relationship can be described as a graph that always starts at point zero and is always a straight line graph.
What is a straight line graph?A straight line graph is defined as the type of graph that is also called a linear graph which shows a relationship between two or more quantities that uses a graphical form of representation.
There are some characteristics that shows that a graph is of proportional relationship which include the following:
The graph always starts from zeroThe graph must be a straight line graphLearn more about graph here:
https://brainly.com/question/25184007
#SPJ1
here is an inequality: -3x > 18 list some values for x that would make this inequality true
Answers
Step-by-step explanation: First, we need to solve this inequality.
When you're asked to solve an inequality like -3x > 18, your goal should be the same as it was when solving equations, to get x by itself on one side.
In this problem since x is being multiplied by -3 on the left side of the inequality, to get x by itself, we divide both sides by -3 but here is the rule you have to watch out for when solving inequalities.
When you divide both sides of an inequality by a negative number, you must switch the direction of the inequality sign. So this greater than in our original problem becomes less than in our second step.
On the left side, the -3's cancel and we're left with
x and on the right side, 18 divided by -3 is -6.
So we have x < -6.
Now, we are asked to state some solutions to the inequality.
The inequality x < -6 means that any number
less than -6 is a solution to the inequality.
For example, -7 is a solution because -7 is less than -6.
-8 is also a solution because -8 is less than -6.
Other possible solutions include -23, -98, -982, and so on.
Any number less than -6 will be a solution.
The figure to the right shows the distance-time graph for a muscle car accelerating from a standstill. Use the information in the figure to answer parts (a) and (b). The table below lists the coordinates of the points.

Answers
The acceleration of the car is 8 m/s^2.
The figure shown in the question is the distance-time graph of a muscle car accelerating from a standstill. The table lists the coordinates of points on the graph.The following observations can be made from the graph and the table: The car is at rest at time t=0 and at distance x=0. It then starts accelerating, and its speed increases uniformly with time. The slope of the distance-time graph is the velocity of the car.
Since the velocity is increasing uniformly, the slope of the graph is a straight line with a positive slope. The area under the graph between two points gives the displacement of the car during that time interval. The displacement can be calculated as the product of the average velocity and the time interval. Using the coordinates in the table, we can calculate the average velocities for each time interval and the displacement during that interval.
(a) The average velocity of the car between t=0 and t=2 is equal to the slope of the graph between the two points (0,0) and (2,32). This can be calculated as the difference in distance divided by the difference in time:Average velocity = (32 - 0) / (2 - 0) = 16 m/sThe displacement during this time interval is given by the area under the graph between the two points:Displacement = (1/2) x 32 x 2 = 32 m
(b) The acceleration of the car is given by the slope of the velocity-time graph. Since the velocity is increasing uniformly with time, the velocity-time graph is also a straight line with a positive slope. The slope of the velocity-time graph is equal to the acceleration. We can calculate the slope of the velocity-time graph between two points using the coordinates in the table. For example, the slope between t=0 and t=2 is given by the difference in velocity divided by the difference in time:Slope = (16 - 0) / (2 - 0) = 8 m/s^2
for more search question acceleration
https://brainly.com/question/30595126
#SPJ8
Write the prime factorization of 45. Use exponents when appropriate and order the factors from least to greatest (for example, 2235)
Answers
The prime factorization of 45 written as exponents from least to greatest is 45 = 3² × 5¹
What is prime factorizationPrime factorization is a way of expressing a number as a product of its prime factors. A prime number is a number that has exactly two factors, which includes 1 and the number.
Using prime factorisation, we shall consider the first five prime numbers which are; 2, 3, 5, 7, and 11.
45 cannot be divided by 2 without a remainder so we use 3;
45/3 = 15
15 can also be divided by 3 so;
15/3 = 5
3 cannot divide 5 without a remainder so we use 5;
5/5 = 1
hence;
45 = 3 × 3 × 5
45 = 3² × 5¹
Therefore, the prime factorization of 45 written as exponents from least to greatest is 45 = 3² × 5¹
Read more about factors here:https://brainly.com/question/1081523
#SPJ1
Which point gives the image (2,-6) after undergoing reflection through the line y=3?

Answers
The required image of the point (2, -6) after undergoing reflection through the line y = 3 is (2, 9).
What is coordinate?Coordinate, is represented as the values on the x-axis and y-axis of the graph. while the coordinate x is called abscissa and the coordinate of the y is called ordinate.
Here,
Given coordinate,
(2, -6),
Given coordinate over the line y = 3 is given as,
⇒(x , y -3)
Now, given the coordinates,
⇒(2, -6 - 3) = (2, -9)
Reflection of the point in line y = 3,
(x, y) ⇒ (x, -y)
(2, -9) ⇒ (2, -(-9)) = (2, 9)
Thus, the required image of the point (2, -6) after undergoing reflection through the line y = 3 is (2, 9).
Learn more about coordinate here:
brainly.com/question/13498438
#SPJ1
The graph below shows the solutions to which inequality?
A. x^2-3x+3 ≥0
B. x² + 3x-3 <0
C. x²-3x+3<0
D. x² + 3x-3>0
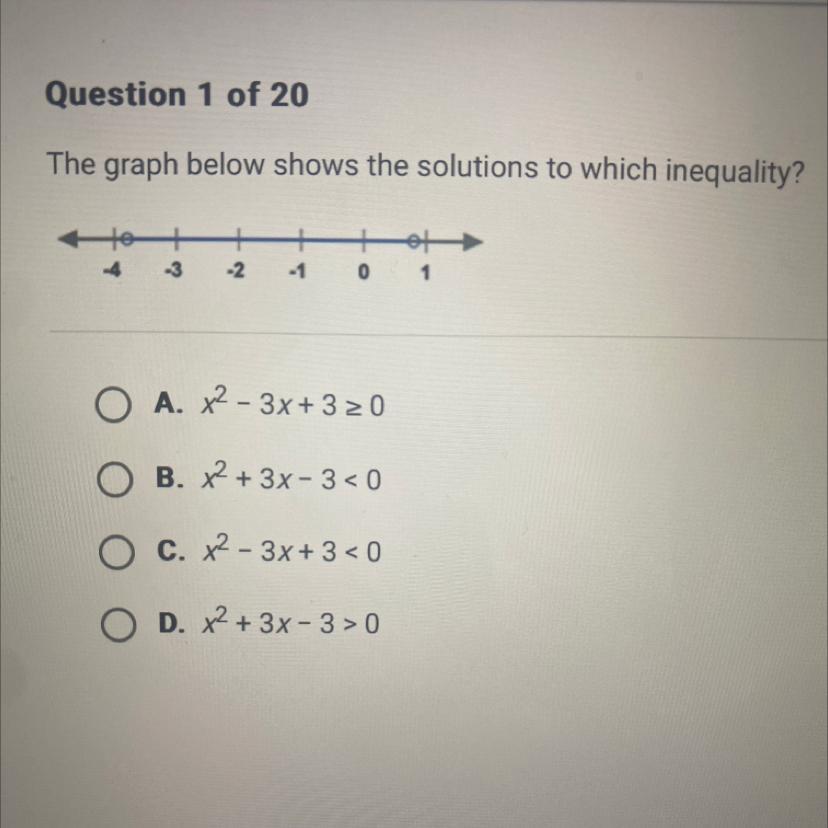
Answers
The inequality expression that corresponds to the solution of the inequality graph is x² + 3x - 3 < 0.
option B.
What is the solution of the inequality?The inequality expression that corresponds to the solution of the inequality graph is determined by simplifying the equations as follows;
The solution of the graph,
x > -4 and x < 1
The first equation with "≥" is ruled out because the graph doesn't have a thick dot.
Let's simplify the second expression;
x² + 3x - 3 < 0
solve using quadratic formula;
x > -3.79 or x < 0.79
The third expression is ruled out since its solution will be complex.
For the last expression;
x² + 3x - 3 > 0
x < -3.79 or x > 0.79
Thus, the correct inequality expression is x² + 3x - 3 < 0.
Learn more about inequality expression here: https://brainly.com/question/25275758
#SPJ1
A store is having a sale on jelly beans and almonds. For 3 pounds of jelly beans and 5 pounds of almonds, the total cost is $27. For 9 pounds of jelly beans and
7 pounds of almonds, the total cost is $51. Find the cost for each pound of jelly beans and each pound of almonds.
Cost for each pound of jelly beans:
Cost for each pound of almonds:
Answers
Answer:
Cost for each pound of jelly beans: $2.75
Cost for each pound of almonds: $3.75
Step-by-step explanation:
Let J be the cost of one pound of jelly beans.
Let A be the cost of one pound of almonds.
Using the given information, we can create a system of equations.
Given 3 pounds of jelly beans and 5 pounds of almonds cost $27:
\(\implies 3J + 5A = 27\)
Given 9 pounds of jelly beans and 7 pounds of almonds cost $51:
\(\implies 9J + 7A = 51\)
Therefore, the system of equations is:
\(\begin{cases}3J+5A=27\\9J+7A=51\end{cases}\)
To solve the system of equations, multiply the first equation by 3 to create a third equation:
\(3J \cdot 3+5A \cdot 3=27 \cdot 3\)
\(9J+15A=81\)
Subtract the second equation from the third equation to eliminate the J term.
\(\begin{array}{crcrcl}&9J & + & 15A & = & 81\\\vphantom{\dfrac12}- & (9J & + & 7A & = & 51)\\\cline{2-6}\vphantom{\dfrac12} &&&8A&=&30\end{array}\)
Solve the equation for A by dividing both sides by 8:
\(\dfrac{8A}{8}=\dfrac{30}{8}\)
\(A=3.75\)
Therefore, the cost of one pound of almonds is $3.75.
Now that we know the cost of one pound of almonds, we can substitute this value into one of the original equations to solve for J.
Using the first equation:
\(3J+5(3.75)=27\)
\(3J+18.75=27\)
\(3J+18.75-18/75=27-18.75\)
\(3J=8.25\)
\(\dfrac{3J}{3}=\dfrac{8.25}{3}\)
\(J=2.75\)
Therefore, the cost of one pound of jelly beans is $2.75.
Given f(x) = x² - 5x - 6 and g(x) =
x² - 6x, what are the domain restrictions
for (-)(x)?
A) x # +6
B) x = 0
C) x = 0,6
D) x = -2,6
Answers
The domain restrictions for (f/g)(x) are (c) x = 0, 6
How to determine the domain restrictions for (f/g)(x)?From the question, we have the following parameters that can be used in our computation:
f(x) = x² - 5x - 6
g(x) = x² - 6x
The composite function (f/g)(x) is calculated as
(f/g)(x) = f(x)/g(x)
substitute the known values in the above equation, so, we have the following representation
(f/g)(x) = (x² - 5x - 6 )/(x² - 6x)
For the domain restriction, we have
x² - 6x = 0
When solved, we have
x = 6 or x = 0
Hence, the domain restrictions for (f/g)(x) are (c) x = 0, 6
Read more about domain at
https://brainly.com/question/27910766
#SPJ1
Question
Given f(x) = x² - 5x - 6 and g(x) = x² - 6x, what are the domain restrictions
for (f/g)(x)?
A) x = +6
B) x = 0
C) x = 0,6
D) x = -2,6
Whats (500 x 2) divided by 2?
Answers
Answer:
500
Step-by-step explanation:
500*2=1000
1000/2=500
Abigail sells dolls at her doll store. If she sells a doll for $55, and there is 8% sales tax, what is the tax amount a customer will pay on one doll? Round your answer to the nearest cent.
help please
Answers
Answer:
The tax amount a customer will pay on one doll is $4.4
Step-by-step explanation:
To find 8% of 55, you multiply .08 by 55, which is 4.4
Please give brainliest!
Identify the graph of the inequality 2(2x-1)+7< 13 or -2x+5-10.

Answers
From the resulting solution, the correct linear inequality graph is Graph C.
Solving inequality expressionGiven the inequality equation below:
2(2x-1)+7< 13 or -2x+5 ≤ -10.
Simplify the expression
2(2x-1)+7< 13
Expand
4x - 2 + 7 < 13
4x + 5 < 13
4x < 13 - 5
4x < 8
x < 2
For the inequality -2x+5 ≤ -10.
-2x+5 ≤ -10
-2x ≤ -15
x ≥ 7.5
Hence the solution to the given system of inequalities are x < 2 and x ≥ 7.5
Learn more on inequality graph here: https://brainly.com/question/24372553
#SPJ1
