Given the diagram below, if CD = x + 4,
DE = 2x + 7, and CE = 7x-25, what is the value
of x?

Answers
9
Explanation :
check out my attached work
Hope it helps, let me know if you have any questions !
Have a nice rest of your day :)

Related Questions
Sima drinks 2.5 litres of water each day.
A full glass holds 125 mililitres of water.
How many full glasses of water does Sima drink each day?
Answers
Answer:
20 glasses a day
Step-by-step explanation:
2.5litres equals 2500millilitres
2500÷125=20
Whats the width of her head
Answers
Answer: 12 inches
Step-by-step explanation:
Answer: 15 cm
Step-by-step explanation:
Which statement describes the graph of X = 4?
A) It is paralel to the x-axis.
B) It has a slope of 4.
C) It is parallel to the y-axis.
D) It passes through the point (0,4).
Answers
Answer:
the answer is D
Step-by-step explanation:
Because the point of x=4 is passed through the point (0,4).
Help with trigonometry homework

Answers
By definition of tangent,
tan(A - π/4) = sin(A - π/4) / cos(A - π/4)
Expand the numerator and denominator using the angle sum identities for sin and cos:
tan(A - π/4) = (sin(A) cos(π/4) - cos(A) sin(π/4)) / (cos(A) cos(π/4) + sin(A) sin(π/4))
Divide through everything on the right by cos(A) cos(π/4):
tan(A - π/4) = (sin(A) / cos(A) - sin(π/4) / cos(π/4)) / (1 + (sin(A) sin(π/4)) / (cos(A) cos(π/4)))
Simplify the sin/cos terms to tan:
tan(A - π/4) = (tan(A) - tan(π/4)) / (1 + tan(A) tan(π/4))
tan(π/4) = 1, so we're left with
tan(A - π/4) = (tan(A) - 1) / (1 + tan(A))
Replace tan(A) with -√15:
tan(A - π/4) = (-√15 - 1) / (1 - √15)
Then the last option is the correct one.
I NEED HELP ASAP
Darwin says that two expressions 3x + 4(2x + 5) and 6x + 5x + 5 are equivalent. Simplify the expressions to determine whether or not Darwin is correct.
Answers
Answer:
Darwin is not correct.
Step-by-step explanation:
3x+4(2x+5) = 6x+5x+5
3x+8x+20 = 11x + 5
11x+20 ≠ 11x+5
if using the method of completing the square to solve the quadratic equation x^2 + 3x +21 =0?
Answers
Answer:
\(x= \dfrac 12 \left( -3 +i5\sqrt 3\right)\\\\x= \dfrac 12 \left( -3 -i5\sqrt 3\right)\)
Step-by-step explanation:
\(~~~~~~x^2 +3x +21 = 0\\\\\implies x^2 +3x = -21\\\\\implies x^2 + 2\cdot \dfrac 32 \cdot x + \left( \dfrac 32 \right)^2 = -21 + \left( \dfrac 32 \right)^2\\\\\implies \left(x + \dfrac 32 \right)^2 = -21+\dfrac 94\\\\\implies \left(x + \dfrac 32 \right)^2 = -\dfrac{75}4\\\\\implies x+ \dfrac 32 = \pm\sqrt{-\dfrac{75}4 \right)\\\\\implies x + \dfrac 32 = \pm i \dfrac{5\sqrt 3}{2}\\\\\implies x = -\dfrac 32 \pm i \dfrac {5\sqrt 3}2\\\\\implies x = \dfrac 12 \left( -3 \pm i5\sqrt 3\right)\)
Find the unit rate (constant of proportionality) of the distance traveled.
Number of hours
0.25 1.5 2.5 3
Distance traveled (km) 3 18 30 36
Answers
Answer:
12.
Step-by-step explanation:
if to re-write the given condition, then
\(\frac{3}{0.25} =\frac{18}{1.5} =\frac{30}{2.5} =\frac{36}{3} ;\)
it is clear, the required constant is 12 (12 per hour).
16 families went on a trip which cost them Rs 2,16,352. How much did each
family pay?
Answers
Given that 16 families went on a trip and the cost of the trip was Rs. 2,16,352.The amount paid by each family is to be determined by unitary method Hence each family paid Rs.13522
Now, let's solve this by using the method of unitary method. To find the cost of 1 family trip, we will divide the total cost of the trip by the number of families.2,16,352 / 16 = 13,522 So, the cost of the trip per family is Rs. 13,522.Hence, each family paid Rs. 13,522 for the trip.
to know more about unitary method
https://brainly.com/question/28276953
Answer:
Step-by-step explanation
1. The total cost of the trip for all 16 families is Rs 2,16,352.
2. To find out how much each family paid, we need to divide the total cost by the number of families: Rs 2,16,352 ÷ 16.
3. When we do the division, we get the result: Rs 13,522.
Now let's check if this result is correct:
1. If each family paid Rs 13,522 for the trip, then the total cost for all 16 families would be: 16 × Rs 13,522 = Rs 2,16,352.
2. This is exactly the same as the total cost given in the problem statement.
So we have shown that each family paid **Rs 13,522** for the trip
Of(x) = x² - 6x-1-
Mark thic and return
24
-10-8-8-22-
-8
-8
-10
2
B
8 10 x
What is the axis of symmetry
Answers
The axis of symmetry of the function f(x) = x² - 6x-1 is equal to 3.
How to determine the axis of symmetry of a quadratic function?In Mathematics, the axis of symmetry of a quadratic function can be calculated by using this mathematical equation:
Axis of symmetry, Xmin = -b/2a
Where:
a and b represents the coefficients of the first and second term in the quadratic function.
By substituting the parameters, we have the following:
Axis of symmetry, Xmin = -b/2a
Axis of symmetry, Xmin = -(-6)/2(1)
Axis of symmetry, Xmin = 6/2
Axis of symmetry, Xmin = 3.
Read more on quadratic functions here: brainly.com/question/14201243
#SPJ1
If AB=BC,AB=4=4x-2,andBC=3x+3,fine the length of AB
Answers
Answer:
18
Step-by-step explanation:
First, I'm assuming AB=4=4x-2 was a typo and it's supposed to be AB = 4x - 2
AB=BC
AB = 4x - 2 BC = 3x + 3
4x - 2 = 3x + 3
Solve for x Add 2 to each side
4x - 2 = 3x + 3
4x - 2 + 2 = 3x + 3 + 2
4x = 3x + 5 Subtract 3x from each side.
4x - 3x = 3x- 3x + 5
4x - 3x = 5
x = 5
Now plug back in to the original equations
AB = 4x - 2 BC = 3x + 3
AB = 4 (5) - 2 BC = 3(5) + 3
AB = 20 - 2 BC = 15 + 3
AB = 18 BC = 18
So AB is 18
Can you guys help me pls

Answers
Explanation: When answering a question like this check to see if the line is a negative slope : or a positive slope:
use the steps: RISE-over-RUN
FOR EXAMPLE- this would be rise 3 run 1
3/1 or 3 :)
A wheel has a radius of 33 cm and completes 12 revolutions in 1 minute. a) determine the angular velocity of the wheel in radians/second. b) If the wheel is moving for 5 minutes, how far does it travel?
Answers
Answer:
a) The angular velocity is 0.4π radians/second ⇒1.25664 radians/second
b) The wheel travels 124.4071 meters in 5 minutes ⇒ 39.6π meters
Step-by-step explanation:
The angular velocity ω = 2 π n ÷ t, where
n is the number of revolution t is the time in secondThe distance that moving by the angular velocity is d = ω r t, where
r is the radius of the circle in metera)
∵ A wheel completes 12 revolutions in 1 minute
∴ n = 12
∴ t = 1 minute
→ Change the minute to seconds
∵ 1 minute = 60 seconds
∴ t = 60 seconds
→ Substitute n and t in the rule above
∵ ω = 2 (π) (12) ÷ 60
∴ ω = 24π ÷ 60
∴ ω = 0.4π radians/second
∴ The angular velocity is 0.4π radians/second ⇒1.25664 radians/second
b)
→ To find the distance in 5 minutes multiply ω by the radius by the time
∵ The wheel has a radius of 33 cm
∴ r = 33 cm
→ Change it to meter
∵ 1 m = 100 cm
∴ r = 33 ÷ 100 = 0.33 m
∵ t = 5 minutes
→ Change it to seconds
∴ t = 5 × 60 = 300 seconds
→ Substitute them in the rule of the distance above
∵ d = 0.4π (0.33) (300)
∴ d = 39.6π meters ⇒ 124.407 meters
∴ The wheel travels 124.4071 meters in 5 minutes ⇒ 39.6π meters
can someone help me with this question?

Answers
Yolanda saves all the money from a regular baby-sitting job. The money in her savings account is increasing according to the equation y = 6x + 50, where x = number of hours worked and y = savings in dollars. Which table of values matches this equation?
Answers
Answer:
Table D
Step-by-step explanation:
I have all of the tables listed below and the correct one circled! I used to tutor my cousin about this topic!
I hope this helps and please feel free to comment, ask questions, give feedback, and correct me if I am wrong!
Have a great day!
:)

The 4th table in the option is the correct one.
What is an equation?An equation is a formula that expresses the equality of two expressions, by connecting them with the equals sign =.
Given that, Yolanda saves all the money from a regular baby-sitting job. The money in her savings account is increasing according to the equation y = 6x + 50, where x = number of hours worked and y = savings in dollars.
The given equation is y = 6x + 50
Put x = 0
y = 50
Put x = 5
y = 80
Put x = 10
y = 110
Put x = 15
y = 140
Creating the table,
x y
0 50
5 80
10 110
15 140
Hence, we get the table.
For more references on equation, click;
https://brainly.com/question/29657983
#SPJ2
Translate the given statement into a linear equation in the form
ax + by = c using the indicated variable names. Do not try to solve the resulting equation.
The number of new clients (x) is 149% of the number of old clients (y).
Answers
On solving the provided question ,we can say that The statement "The number of new clients (x) is 149% of the number of old clients (y)" can be written mathematically as: x = 1.49y
what is a sequence?A sequence is a grouping of "terms," or integers. Term examples are 2, 5, and 8. Some sequences can be extended indefinitely by taking advantage of a specific pattern that they exhibit. Use the sequence 2, 5, 8, and then add 3 to make it longer. Formulas exist that show where to seek for words in a sequence. A sequence (or event) in mathematics is a group of things that are arranged in some way. In that it has components (also known as elements or words), it is similar to a set. The length of the sequence is the set of all, possibly infinite, ordered items. the action of arranging two or more things in a sensible sequence.
The statement "The number of new clients (x) is 149% of the number of old clients (y)" can be written mathematically as:
x = 1.49y
-1.49y + x = 0
-149y + 100x = 0
To know more about sequence visit:
https://brainly.com/question/21961097
#SPJ1
The linear equation in the required form is: x - 1.49y = 0
What is linear equation?
A linear equation is a mathematical equation that describes a straight line in a two-dimensional plane. It is an equation of the form:
y = mx + b
Let's start by assigning variables to the given information. We are told that "the number of new clients (x) is 149% of the number of old clients (y)."
Using this information, we can write:
x = 1.49y
To write this equation in the form ax + by = c, we need to move all the variables to one side of the equation and simplify.
Subtracting 1.49y from both sides, we get:
x - 1.49y = 0
So the linear equation in the required form is:
x - 1.49y = 0
To learn more about linear equation from the given link:
https://brainly.com/question/11897796
#SPJ1
4. Approximate the solution to this system of equations.
y = -2x+6
y = 4x - 1
Answers
The solution of the system of linear equations, is (1.167, 3.667).
Given that the system of linear equations, y = -2x+6 and y = 4x - 1, we need to find the solution for the same,
y = -2x+6............(i)
y = 4x - 1.......(ii)
Equating the equations since the LHS is same,
-2x+6 = 4x-1
6x = 7
x = 1.167
Put x = 1.16 to find the value of y,
y = 4(1.16)-1
y = 4.66-1
y = 3.667
Therefore, the solution of the system of linear equations, is (1.167, 3.667).
You can also find the solution using the graphical method,
Plot the equations in the graph, the point of the intersection of both the lines will be the solution of the system of linear equations, [attached]
Hence, the solution of the system of linear equations, is (1.167, 3.667).
Learn more about system of linear equations, click;
https://brainly.com/question/19549073
#SPJ1

-8x+y=6
-8x+3y=-14
How would you solve this using the elimination method? Thanks!
Answers
Answer:
x = -1,375
y = -5
Step-by-step explanation:
{-8x + y = 6, / : (-1)
{-8x + 3y = -14;
Multiply the first equation by -1, so that we could eliminate 8x:
+ {8x - y = -6,
{-8x + 3y = -14;
----------------------
4y = - 20 / : 4
y = -5
Now, make x the subject from the first equation (you can do it from the 2nd one instead):
8x = -6 + y / : 8
x = -0,75 + 0,125y
x = -0,75 + 0,125 × (-5) = -0,75 - 0,625 = -1,375
Kyle works at a donut factory, where a 10-oz cup of coffee costs 95¢, a 14-oz cup costs $1.15, and a 20-oz cup costs $1.50. During one busy period, Kyle served 14 cups of coffee, using 204 ounces of coffee, while collecting a total of $16.70. How many cups of each size did Kyle fill?
Kyle filled ___ 10-oz cup(s), ___ 14-oz cup(s), and ___ 20-oz cup(s).
Answers
Answer:
Step-by-step explanation:
Lets assume that Kyle fill "a" 10-oz cups of coffee, "b" 14-oz cups of coffee and "c" 20 oz cups of coffee.
a + b + c = 16 (1)
10*a + 14*b + 20*c = 224 (2)
0.95*a + 1.15*b + 1.50*c = 18.60 (3)
Now, multiplying equation (1) by 10 and subtracting it from equation (2), we get
4b + 10c = 64 (4)
Again, multiplying equation (1) by 0.95 and substracting it from equation (3), we get,
0.2b + 0.55c = 3.4 (5)
Now,
Multiplying equation (5) by 20 and subtracting it from equation (4), we get
-c = -4,
Hence, c= 4
Putting this value in equation (4),
4b + 40 = 64
Hence, 4b = 24
So, b = 6
Again, putting the values of b and c in equation (1),
a + 6 + 4 = 16
Thus,
a = 6
Hence, the solution is
a = 6, 10oz cups of coffee
b = 6, 14 oz cups of coffee
c = 4, 20 oz cups of coffee
Can I please get some help I’ve been stuck on this question for a while!

Answers
Using the radius of the Ferris wheel and the angle between the two positions, the time spent on the ride when they're 28 meters above the ground is 12 minutes
How many minutes of the ride are spent higher than 28 meters above the ground?The radius of the Ferris wheel is 30 / 2 = 15 meters.
The highest point on the Ferris wheel is 15 + 4 = 19 meters above the ground.
The time spent higher than 28 meters is the time spent between the 12 o'clock and 8 o'clock positions.
The angle between these two positions is 180 degrees.
The time spent at each position is 10 minutes / 360 degrees * 180 degrees = 6 minutes.
Therefore, the total time spent higher than 28 meters is 6 minutes * 2 = 12 minutes.
Learn more on a Ferris wheel here;
https://brainly.com/question/30524034
#SPJ1
Determine the monthly principal and interest payment for a 15 -year mortgage when the amount financed is $85,000 and the annual percentage rate (APR) is %.7.0
Answers
Monthly Mortgage Payment is $495.88
Mortgage is a long-term amortized loan where loan is provided to buy certain capital asset and pay back total sum due in small periodic annuities. In Mortgage title of asset lies with lender and passes to borrower after complete mortgage payment.
Hence,
Mortgage Amount is $77,000
Monthly Payment for each $1,000 is $6.44
Monthly Mortgage Payment is $495.88
To learn more about Mortgage visit: https://brainly.com/question/8845095
#SPJ1

Determine the missing factor in ■ × 4.2 = 16.8.
Answers
Point M is located at (6, 7) on the coordinate plane. Point N is located 5 units to the left and 2 units down from point
M.

Answers
Answer:
(1,5)
Step-by-step explanation:
x:
6-5=1
y:
7-2=5
PLEASE HELP ME
An article claimed the state's typical price of a gallon of gasoline is $2.69. The prices from 5 gas stations surveyed were $2.79, $2.99, $2.69, $2.89, and $2.69.
According to this data, what is wrong with the article's statement?
Answers
This statement in the article is wrong because $2.69 is not the mean price ($2.81)
How to determine what is wrong with the data?The prices from 5 gas stations surveyed are given as:
$2.79, $2.99, $2.69, $2.89, and $2.69.
There are no outliers in the dataset
So, the dataset can be summarized by the mean
The mean is
Mean = Sum/Count
So, we have
Mean = ($2.79+ $2.99+ $2.69+ $2.89+$2.69)/5
Evaluate
Mean = 2.81
The article quoted $2.69 as the typical price
This statement in the article is wrong because $2.69 is not the mean price ($2.81)
Read more about mean at:
https://brainly.com/question/20118982
#SPJ1
The figure above shows the graph of f ', the derivative of a twice-differentiable function f, on the interval
[–3, 4]. Answer the following questions based on the graph of f ′.
a) Find all x-coordinates at which f has critical values and identify them as a relative minimum,
relative maximum, or neither. Justify your answer.
b) On what open intervals contained in [–3, 4] is the graph of f both concave up and decreasing?
Justify your answer.
c) Find the x-coordinates of all points of inflection on the graph of f

Answers
Step-by-step explanation:
a) The x-coordinates at which f has critical values can be found by looking at the x-coordinates of the points where the graph of f' changes from increasing to decreasing or vice versa. These are the points where the graph of f' crosses the x-axis.
Based on the graph of f', we can see that the critical points occur at x = -2, -1, and 2. To determine if these are relative minimum, relative maximum, or neither, we need to examine the second derivative of f. If the second derivative is positive at a critical point, then the point is a relative minimum. If the second derivative is negative at a critical point, then the point is a relative maximum. If the second derivative is zero at a critical point, then it's neither.
b) The graph of f is concave up when the second derivative is positive, and the graph of f is decreasing when the first derivative is negative. Based on the graph of f', we can see that the graph of f is concave up on the open intervals (-3,-2) and (1,2) and decreasing on the open intervals (-infinity,-3) and (-2,-1) U (2,4) U (infinity,4)
c) The x-coordinates of all points of inflection on the graph of f are the points where the concavity of the graph changes. We can see that a point of inflection occurs at x = -1 and x = 2
what is the property of 3x(5x7)=(3x5)7
Answers
The property you are referring to is called the associative property of multiplication. According to this property, when multiplying three numbers, the grouping of the numbers does not affect the result. In other words, you can change the grouping of the factors without changing the product.
In the equation you provided: 3x(5x7) = (3x5)7
The associative property allows us to group the factors in different ways without changing the result. So, whether we multiply 5 and 7 first, or multiply 3 and 5 first, the final product will be the same.
What is the answers to Part A, B, and C ?

Answers
Part a: The data points appear to follow an exponential pattern. This is because the balance is increasing at a rate that is proportional to the current balance.
How to explain the informationPart b: The equation of the best fit is y = 50(1.06)^x. This can be found using a variety of methods, including graphing the data points and fitting a curve to them, or using a statistical software package.
Part c: When x = 32, y = 50(1.06)^32 = $2,499.82.
Years since 1990, x 0 5 10 15 20 25 30
Balance, y $50 $62.31 $77.65 $96.76 $120.59 $150.27 $187.27 $2,499.82
The equation of the fitted curve is y = 50(1.06)^x.
Learn more about equations on
https://brainly.com/question/2972832
#SPJ1
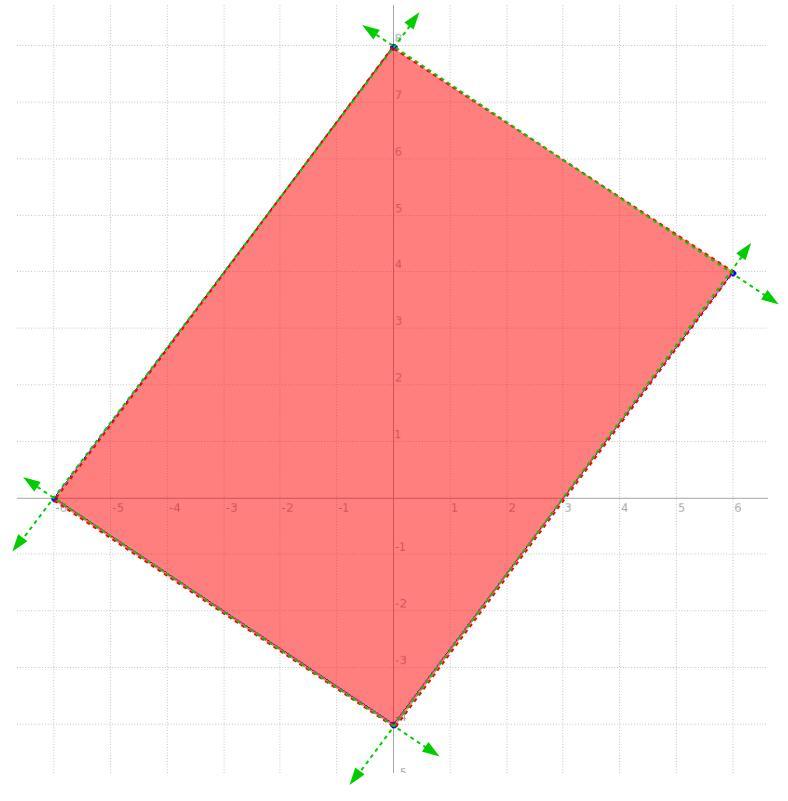
HELP PLEASE I DONT GET THIS

Answers
so the idea being, we have a system of equations of two variables and 4 equations, each one rendering a line, for this case these aren't equations per se, they're INEquations, so pretty much the function will be the same for an equation but we'll use > or < instead of =, but fairly the function is basically the same, the behaviour differs a bit.
we have a line passing through (-6,0) and (0,8), side one
we have a line passing through the x-axis and -6, namely (-6,0) and the y-axis and -4, namely (0,-4), side two
we have a line passing through (0,-4) and (6,4), side three
now, side four is simply the line connecting one and three.
the intersection of all four lines looks like the one in the picture below, so what are those lines with their shading producing that quadrilateral?
well, we have two points for all four, and that's all we need to get the equation of a line, once we get the equation, with its shading like that in the picture, we'll make it an inequality.
\((\stackrel{x_1}{-6}~,~\stackrel{y_1}{0})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{8}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{8}-\stackrel{y1}{0}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{(-6)}}} \implies \cfrac{8 -0}{0 +6} \implies \cfrac{ 8 }{ 6 } \implies \cfrac{4}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{0}=\stackrel{m}{ \cfrac{4}{3}}(x-\stackrel{x_1}{(-6)}) \implies y -0 = \cfrac{4}{3} ( x +6) \\\\\\ y=\cfrac{4}{3}x+8\hspace{5em}\stackrel{\textit{side one} }{\boxed{y < \cfrac{4}{3}x+8}}\)
\(\rule{34em}{0.25pt}\\\\ (\stackrel{x_1}{-6}~,~\stackrel{y_1}{0})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{-4}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{-4}-\stackrel{y1}{0}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{(-6)}}} \implies \cfrac{-4 -0}{0 +6} \implies \cfrac{ -4 }{ 6 } \implies - \cfrac{2}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{0}=\stackrel{m}{- \cfrac{2}{3}}(x-\stackrel{x_1}{(-6)}) \implies y -0 = - \cfrac{2}{3} ( x +6) \\\\\\ y=-\cfrac{2}{3}x-4\hspace{5em}\stackrel{\textit{side two} }{\boxed{y > -\cfrac{2}{3}x-4}} \\\\[-0.35em] \rule{34em}{0.25pt}\)
\(\stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{4}-\stackrel{y1}{(-4)}}}{\underset{\textit{\large run}} {\underset{x_2}{6}-\underset{x_1}{0}}} \implies \cfrac{4 +4}{6 -0} \implies \cfrac{ 8 }{ 6 } \implies \cfrac{4}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-4)}=\stackrel{m}{ \cfrac{4}{3}}(x-\stackrel{x_1}{0}) \implies y +4 = \cfrac{4}{3} ( x -0) \\\\\\ y=\cfrac{4}{3}x-4\hspace{5em}\stackrel{ \textit{side three} }{\boxed{y > \cfrac{4}{3}x-4}} \\\\[-0.35em] \rule{34em}{0.25pt}\)
\((\stackrel{x_1}{6}~,~\stackrel{y_1}{4})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{8}) ~\hfill~ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{8}-\stackrel{y1}{4}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{6}}} \implies \cfrac{ 4 }{ -6 } \implies - \cfrac{2}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{4}=\stackrel{m}{- \cfrac{2}{3}}(x-\stackrel{x_1}{6}) \\\\\\ y=-\cfrac{2}{3}x+8\hspace{5em}\stackrel{ \textit{side four} }{\boxed{y < -\cfrac{2}{3}x+8}}\)
now, we can make that quadrilateral a trapezoid by simply moving one point for "side four", say we change the point (0 , 8) and in essence slide it down over the line to (-3 , 4). Notice, all we did was slide it down the line of side one, that means the equation for side one never changed and thus its inequality is the same function.
now, with the new points for side for of (-3,4) and (6,4), let's rewrite its inequality
\((\stackrel{x_1}{-3}~,~\stackrel{y_1}{4})\qquad (\stackrel{x_2}{6}~,~\stackrel{y_2}{4}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{4}-\stackrel{y1}{4}}}{\underset{\textit{\large run}} {\underset{x_2}{6}-\underset{x_1}{(-3)}}} \implies \cfrac{4 -4}{6 +3} \implies \cfrac{ 0 }{ 9 } \implies 0\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{4}=\stackrel{m}{ 0}(x-\stackrel{x_1}{(-3)}) \implies y -4 = 0 ( x +3) \\\\\\ y=4\hspace{5em}\stackrel{ \textit{side four changed} }{\boxed{y < 4}}\)
What is the image of (2, 10) after a dilation by a scale factor of 1/2 centered at the origin?
Answers
Answer: (1,5)
Analysis = \(\frac{1}{2}(2,10)\)
\(=(\frac{1}{2}\times2,\frac{1}{2}\times10)\)
\(=(1,5)\)
I hope this helps you :D
2 + 2. what is the sum
Answers
Answer: 4
Step-by-step explanation:
Answer:4
2+2=4 if I have two apples and pick up two more I now have 4 total
1. Match the picture of the triangle to the correct name for its center,

Answers
1. d 2. a 3. c 4. b
Step-by-step explanation:\(1.d\ \{The\ intersection\ of\ three\ high\ lines\}\)
\(2.\ a\)
\(3.\ C\)
\(4.\ b\ \{The\ intersection\ of\ three\ angular\)
\(bisectors\}\)
I hope this helps you
:)
Answer:
dbcaStep-by-step explanation:
Various centers are defined for a triangle, depending on how they're constructed. Here, you're asked to match the construction with the name.
__
OrthocenterThe orthocenter is the intersection of the altitudes of the triangle. Each altitude intersects a vertex and is orthogonal to the opposite side. The orthocenter will not be inside the triangle if the triangle is obtuse. The orthocenter of a right triangle is the right-angle vertex.
Figure D depicts the intersection of altitudes.
__
IncenterThe incenter is the center of an inscribed circle of a triangle. The incenter must be the same distance from each side, so will be at the point of intersection of the angle bisectors. It always lies inside the triangle.
Figure B depicts the intersection of angle bisectors.
__
CentroidThe centroid is the "center of gravity" of the triangle, the point at which the triangle could be balanced. Each median divides the triangle into two equal areas, so the intersection of medians marks a spot with equal area (weight) in every pair of opposite directions.
Figure C depicts the intersection of medians.
__
CircumcenterThe circumcenter is the center of a circle that circumscribes the triangle. It is equidistant from the three vertices, so lies on the intersection of the perpendicular bisectors of the sides. It will lie outside the triangle for obtuse triangles. It is the midpoint of the hypotenuse of a right triangle.
Figure A depicts the intersection of perpendicular bisectors of the sides.