helen plans on reading 2 books this year. if there are 7 books on her reading list to choose from, how many different book choice combinations are possible?
Answers
There are 21 different book choice combinations possible for Helen to select 2 books from a list of 7 books.
To calculate the number of different book choice combinations, we can use the formula for combinations, which is given by C(n, r) = n! / (r!(n-r)!), where n is the total number of items and r is the number of items to be selected. In this case, Helen has 7 books to choose from and she plans on reading 2 books. So, we can substitute n = 7 and r = 2 into the formula.
C(7, 2) = 7! / (2!(7-2)!) = (7 * 6 * 5!) / (2 * 1 * 5!) = (7 * 6) / (2 * 1) = 42 / 2 = 21.
Therefore, there are 21 different book choice combinations possible for Helen. She can select any 2 books out of the 7 books on her reading list in 21 different ways.
Learn more about combinations here:
https://brainly.com/question/30777794
#SPJ11
Related Questions
How can you determine whether two circles are congruent?
Answers
Answer:
If the diameter or radius of one circle is the same as another circle they are congruent.
12. Charlie's Pancake House has decided to increase all of its menu prices by 8%. Let
x represent the original price of an item on the menu. Which expressions can the owner
use to calculate each item's new menu price?
Select two answer choices.
Answers
To calculate the new prices you would use the equation p = 1.08x
You said select two answer choices, but I’m not sure if you mean two ways of answering.
I suppose you could divide x by (1.0 / 1.08) by doing x (1.0 / 1.08)^-1, but I don’t think that would be a rational way of doing this.
Hope this was helpful.
Wyatt says that both red lines are lines of symmetry. Is he correct? Why or why not?

Answers
Answer:
Step-by-step explanation:
There is only one line of symmetry:
because the one that is vertical is not representing symmetry.
What is the area of this figure? Enter your answer in the box. cm2
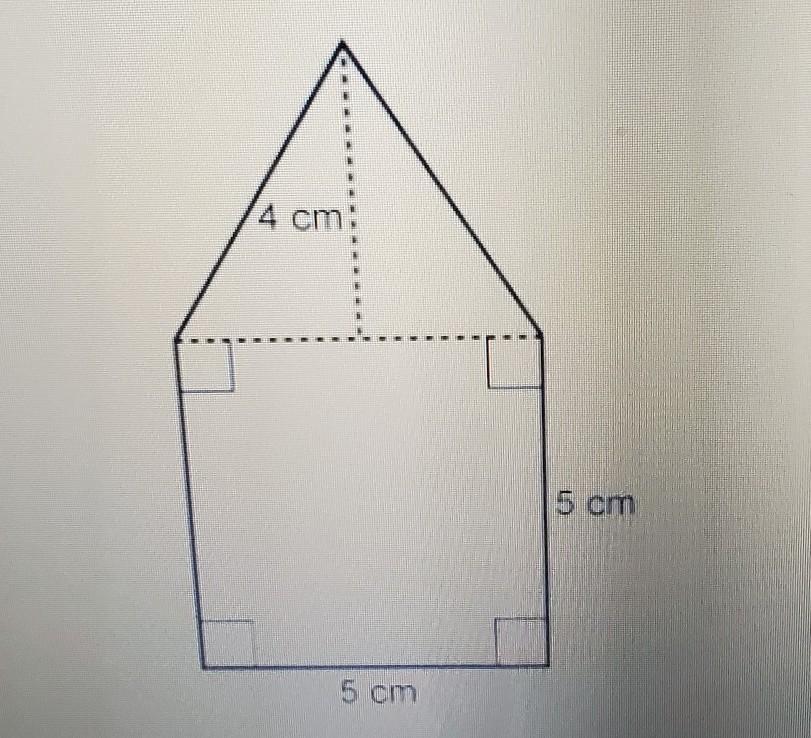
Answers
Answer:
35 cm²Step-by-step explanation:
Area of the bottom part (the square) is:
5*5 = 25 cm²Area of the top part (the triangle) is:
1/2*5*4 = 10 cm²Total area is:
25 + 10 = 35 cm²Answer:
The area of this figure is 35 cm².
Step-by-step explanation:
Area of the square part (lower part)= 5²=25cm²Area of the triangular part (upper part)=1/2×4×5=10cm²Total Area= (Area of the square+Area of the triangle) =(10cm²+25cm²)=35cm²Leroy, Brian, and Elena were hungry one afternoon, and they wanted a healthy snack. They decided to split one cup of carrots and one cup of celery.
Answers
Leroy, Brian, and Elena were feeling hungry one afternoon and opted for a healthy snack. They agreed to split one cup of carrots and one cup of celery amongst themselves.
To ensure an equitable distribution, each person would receive an equal portion of the snacks. As there are three individuals, they would divide the cups into three equal parts.
Thus, each person would receive 1/3 cup of carrots and 1/3 cup of celery. This way, they could enjoy their snack together while maintaining a balanced and healthy portion size.
By dividing the cups equally among Leroy, Brian, and Elena, they could satisfy their hunger and savor the nutritional benefits of their shared snack.
To learn more more about portion click here:brainly.com/question/31070184
#SPJ11
Which statement is true?
A. cosine squared 47 degrees equals Start Fraction 1 plus cosine 94 degrees over 2 End Fraction
B. cosine left parenthesis Start Fraction pi over 4 End Fraction right parenthesis equals plus or minus Start Root Start Fraction 1 plus cosine left parenthesis Start Fraction pi over 8 End Fraction right parenthesis over 2 End Fraction End Root
C. tangent 34 degrees equals Start Fraction 2 tangent 68 degrees over 1 minus tangent squared 68 degrees End Fraction
D. sine left parenthesis Start Fraction pi over 6 End Fraction right parenthesis equals cosine squared left parenthesis left parenthesis Start Fraction pi over 12 End Fraction minus sine squared left parenthesis Start Fraction pi over 12 End Fraction

Answers
The correct trigonometric function cos²47° = (1 + cos94°)/2 thus, option (A) is correct.
What is a trigonometric function?The fundamental 6 functions of trigonometry have a range of numbers as their result and a domain input value that is the angle of a right triangle.
The trigonometric function is very good and useful in real-life problems related to the right-angle triangle.
It is known that,
cos2x = 2cos²x - 1
2cos²x = 1 + cos2x
cos²x = (1 + cos2x)/2
Put x = 47°
cos²47° = (1 + cos94°)/2
Hence "The correct trigonometric function cos²47° = (1 + cos94°)/2".
For more information about the trigonometric function,
https://brainly.com/question/14746686
#SPJ1
Please help! *Excel Formulas* "Assume the compounding period suggested by the problem. Assume that payments are end of period payments" 6. Assume you are age 78 . You plan on living to age 100 . If you have $725,000 on which you can earn an APR of 6.25%, how much can you take out per month in order to completely exhaust your savings in 22 years assuming monthly compounding?
Answers
An initial amount of $725,000, an APR of 6.25%, and a desired time frame of 22 years, the monthly withdrawal amount would be approximately $4,491.95.
To calculate the monthly withdrawal amount that would completely exhaust your savings in 22 years, we can use the present value of an ordinary annuity formula. The present value (PV) represents the initial amount you have, the interest rate per period (i) is the monthly interest rate, and the number of periods (n) is the total number of months.
Here's the step-by-step calculation:
Convert the APR to a monthly interest rate:
Monthly interest rate (i) = Annual interest rate / Number of compounding periods per year
i = 6.25% / 12 = 0.0625 / 12 = 0.00521 (rounded to 5 decimal places)
Determine the total number of periods:
Total number of periods (n) = Number of years * Number of compounding periods per year
n = 22 * 12 = 264
Use the present value of an ordinary annuity formula to calculate the monthly withdrawal amount (PMT):
PMT = PV / [(1 - (1 + i)^(-n)) / i]
In this case, PV = $725,000
PMT = $725,000 / [(1 - (1 + 0.00521)^(-264)) / 0.00521]
Calculate the monthly withdrawal amount using a financial calculator or spreadsheet software:
PMT ≈ $4,491.95 (rounded to the nearest cent)
Therefore, you can withdraw approximately $4,491.95 per month to completely exhaust your savings in 22 years assuming monthly compounding.
Learn more about approximately here:
https://brainly.com/question/31695967
#SPJ11
44. Which number line represents
the solutions for the inequality
45 + 4x> 125?
А
18 19 20
21
22 23 24 25 26
B
18 19 2022 23 24 25 26
21
с
22 23 24 25 26
18 19 20 21
D
18 19 20 21 22
23 24 25 26
Answers
Step-by-step explanation:
=> 45 + 4x > 125
=> 4x > 125 - 45
=> 4x > 30
=> x > 30/4
=> x > 7.5
Use the reverse order of operation to solve this problem.
2m = 1
Answers
Answer: m = 1/2 or 0.5
Step-by-step explanation:
The order of operation within this problem is multiplication meaning we must divide instead.
2m = 1
2m/2 = 1/2
m = 1/2 or 0.5
Aaron is designing a party game in which he needs exactly 24 possible outcomes. which sets of actions can he use to have a statistically fair game?
Answers
If Aaron is designing a party game in which he needs exactly 24 possible outcomes, then he can use the following sets of actions to have a statistically fair game from the Statistics point of view,
Toss a coin twice, and then then roll a 6-sided number cube.
How can he play a statistically fair game to get exactly 24 outcomes?
The game has 24 alternative outcomes, as far as we know. The next step is to identify a series of activities that produces 24 distinct outcomes with equal probabilities.
The first of the alternatives is the only one with a sample space of 24 elements.
Flip two coins, then roll a D6.
The results of each coin toss are 2: (tails and heads).
There are 6 outcomes for the D6: (1, 2, 3, 4, 5, 6)
The combined outcomes of the two throws and rolling the number are then given by the product between the numbers of outcomes for each individual part, as solved below:
C = 2 × 2 × 6
C = 24
Thus, by tossing a coin twice, and then then rolling a 6-sided number cube, Aron can play a statistically fair game if h needs exactly 24 outcomes.
Learn more about outcomes here:
https://brainly.com/question/9222927
#SPJ1
The price of a technology stock was $9.68 yesterday. Today, the price fell to $9.61. Find the percentage decrease. Round your answer to the nearest tenth of a percent.
Answers
Answer:
Use Ratio method
9.68 : 100
9.61 : x
Cross multiply
9.68x=961
x=961/9.68
x=99.2768595
Rounded off its 99%, so there has been a 100-99=1% percentage loss
Step-by-step explanation:
round off 7284 to 1sf
Answers
Answer:
7000
Step-by-step explanation:
This is because when you round to the significant figure, you basically look at any digits at the start of the number, which isn't zero. In this case, it would be in the thousands place 7284. So you round 7284 to the nearest thousands, which, would be 7000
If ST=SV=90, TU=7x, and UV=x+84, what is the value of x?
Answers
a golf ball has a circumference of 13.408 centimeters, and 336 dimples on its surface. approximately how many dimples per square centimeter are on the surface of a golf ball?a. 0.170b. 1.468c. 4.268d. 5.872
Answers
Number of dimples per square centimeter are on the surface of a golf ball is,
⇒ 5.872
What is an expression?Mathematical expression is defined as the collection of the numbers variables and functions by using operations like addition, subtraction, multiplication, and division.
Given that;
A golf ball has a circumference of 13.408 centimeters.
And, 336 dimples on its surface.
Now, We know that;
Circumference of circle = 2πr
Here, A golf ball has a circumference of 13.408 centimeters.
Hence, We get;
Circumference of circle = 2πr
13.408 = 2 × 3.14 × r
13.408 = 6.28 × r
r = 2.14 cm
Now, The surface area of golf ball is,
⇒ 4πr²
⇒ 4 × 3.14 × 2.14²
⇒ 56.76 cm²
Thus, Number of dimples per square centimeter are on the surface of a golf ball is,
⇒ 36 / 56.76
⇒ 5.872
Learn more about the mathematical expression visit:
brainly.com/question/1859113
#SPJ1
A circular "No U-Turn" road sign has a diameter of 20 inches.
Which measurement is closest to the area of the sign in square inches?
O 62.8 in 2
0 125.6 in 2
O 314 in.
O 1256 in 2
Answers
Answer:
314
Step-by-step explanation:
d=20
20/2=10
10x10=100
A=pi r2
A=3.14x100
A=314
a local news outlet reported that 56% of 600 randomly sampled kansas residents planned to set off fireworks on july 4th. compute the 98% confidence interval for the true proportion.
Answers
The 98% confidence interval for the true proportion is (0.506, 0.614).
Given that a local news outlet reported that 56% of 600 randomly sampled Kansas residents planned to set off fireworks on July 4th and we need to compute the 98% confidence interval for the true proportion.
The formula to find the confidence interval is given by;
\(CI = \hat{p} \pm z_{\alpha/2} \times \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\)
Where,
\(\hat{p}\) = Sample proportion\(n\)
= Sample size\(z_{\alpha/2}\)
= Critical value for the confidence level\(\alpha\)
= Level of significance
Let's put the given values in the above formula:
\(\hat{p} = 56\%
= 0.56\)\(n
= 600\)\(\alpha
= 0.02\) (As the level of significance is 1 - 0.98)\(z_{\alpha/2}\)
= 2.33 (From standard normal distribution table)N
ow, we will compute the confidence interval by putting the above values in the formula;
\(\begin{aligned}CI
= \hat{p} \pm z_{\alpha/2} \times \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \\
= 0.56 \pm 2.33 \times \sqrt{\frac{0.56(1-0.56)}{600}} \\
= 0.56 \pm 0.054 \\
= (0.506, 0.614) \end{aligned}\)
Therefore, the 98% confidence interval for the true proportion is (0.506, 0.614).
Know more about 98% confidence interval here:
https://brainly.com/question/17097944
#SPJ11
4. Find the value of x. a. 124 b. 63 c. 119 d. 56

Answers
Answer:
119
Step-by-step explanation:
You would do
180 - (63+56) = 119
victor Donates $25 each month to a children's Charity and Donates a bounus 100$
Answers
Answer:
he donates 125
Step-by-step explanation:
Consider a pair of integers, (a, b). The following operations can be performed on (a, b) in any order, zero or more times: • (a, b)(a + b, b) • (a, b) → (a, a + b) Return a string that denotes whether or not (a, b) can be converted to to (c,d) by by performing zero or more of the operations specified above. Example (a, b) = (1, 1) (c,d) = (5,2) Perform the operation (1,1 + 1) to get (1, 2), perform the operation (1 + 2, 2) to get (3, 2), and perform the operation (3+2, 2) to get (5,2). Alternatively, the first operation could be (1+1, 1) to get (2, 1) and so on. The diagram below demonstrates the example representing the pairs as Cartesian coordinates: 5 4 3 2 (1,1+1) (3+2,2) (1+2,2) Goal 1 a Start(1,1) b 1 2 3 4 5 Function Description Complete the function is possible in the editor below. isPossible has the following parameter(s): int a: first value in (a, b) int b: second value in (a, b) int c: first value in (c,d) int d: second value in (c,d) Returns: str: Return 'Yes' if (a, b) can be converted to (c,d) by performing zero or more of the operations specified above, or 'No' if not Constraints • 1 sa,b,c,ds 1000
Answers
We return "Yes"; otherwise, we return "No".
What is probability?
Probability is a measure of the likelihood of an event occurring. It is expressed as a number between 0 and 1, where 0 means that the event is impossible and 1 means that the event is certain to occur.
To solve this problem, we can work backward from (c,d) to (a,b) and check if each step is valid. Specifically, we can use the following observations:
If c < a or d < b, it is impossible to reach (c,d) from (a,b) using the given operations.
If c - a = d - b, we can reach (c,d) from (a,b) using only the second operation. Specifically, we can perform the operation (a, a+b) repeatedly until we reach (c,d).
If c - a != d - b, we can reach (c,d) from (a,b) using a combination of the two operations. Specifically, we can perform the first operation (a,b) -> (a+b,b) repeatedly until we get to a point where c - a = d - b, and then use the second operation to get to (c,d).
Here, we first check if it is impossible to reach (c,d) from (a,b) using the observations above. If not, we perform the second operation as many times as possible to reduce the difference between c and a, and d and b. Once this is done, we check if we have arrived at (a,b).
Therefore, we return "Yes"; otherwise, we return "No".
To learn more about probability from the given link -
https://brainly.com/question/30034780
#SPJ1
Diana observes a snail moving away from herself. The snail moves 2 inches in 4 seconds. The snail is 9 inches away from Diana after 3 seconds. Write an equaton for the snail's distance from Diana, y, as a function of time, x.
Answers
After 10 seconds, the snail is 14 inches away from Diana. Let's assume that Diana is at the origin (0,0) and the snail moves at a constant speed. Let's consider the snail is at point (x, y) and Diana is at the origin (0,0). The snail is moving away from Diana at a constant speed. It moves 2 inches in 4 seconds.
Then the distance traveled by the snail in 1 second is
= 2/4inches
= 0.5 inches.
So, the distance the snail travels from (0,0) in x seconds is 0.5x. After 3 seconds, the snail moves
= 0.5(3)
= 1.5 inches away from Diana, and its distance from her is 9 inches.
So, we have y = 9 + 0.5x. This is the equation for the snail's distance from Diana, y, as a function of time, x.
We can see that the equation y = 9 + 0.5x provides the snail's distance from Diana. Here, y is the distance between Diana and the snail and x is the current time. We can observe that the snail moves at a constant pace of 0.5 inches per second since the coefficient of x is equal to 0.5. The constant term in the equation is 9, which stands for the separation between Diana and the snail at the initial value of x, or 0, the starting point.
Therefore, we can infer that the distance between the snail and Diana, y, as a function of time, x, is represented by the equation y = 9 + 0.5x. The distance between Diana and the snail can be calculated at any time using this equation. The distance between Diana and the snail after 10 seconds, for instance, can be calculated using this equation.
For this,
we substitute x = 10 in the equation and get
y = 9 + 0.5(10)
= 14.
Therefore, after 10 seconds, the snail is 14 inches away from Diana.
To know more about the constant speed, visit:
brainly.com/question/24909693
#SPJ11
Find avarage value of function f(x,y)=9x+2y over 0⩽x⩽3,0≤y≤9 A) 245 ? b) Evaluate ∫−310∫−10−45xdydx c) 1365 ? C) Write equation double integral with order of Integrals reversed ∫03∫07y/3dxdy A) ∫01∫3x113dydx ?
Answers
a) The average value of f(x, y) = 9x + 2y over the region 0 ≤ x ≤ 3 and 0 ≤ y ≤ 9 is 486.
b) The value of the double integral is 547.5.
c) The value of the double integral with the order of integrals reversed is 10.5.
To find the average value of the function f(x, y) = 9x + 2y over the region 0 ≤ x ≤ 3 and 0 ≤ y ≤ 9, we need to calculate the double integral of the function over the given region and divide it by the area of the region.
a) Average value of f(x, y) = 9x + 2y is 245.
Average value of f(x, y) = (1 / Area of Region) ∫[0, 3]∫[0, 9] (9x + 2y) dy dx
The area of the region is given by:
Area = ∫[0, 3]∫[0, 9] 1 dy dx = 3 * 9 = 27
Now, let's calculate the double integral:
∫[0, 3]∫[0, 9] (9x + 2y) dy dx
= ∫[0, 3] (9xy + y²/2) | [0, 9] dx
= ∫[0, 3] (81x + 81/2) dx
= [81x²/2 + 81x/2] | [0, 3]
= (81(3)²/2 + 81(3)/2) - (81(0)²/2 + 81(0)/2)
= (81(9)/2 + 81(3)/2)
= (729/2 + 243/2)
= 972/2
= 486
The average value of f(x, y) = 9x + 2y over the region 0 ≤ x ≤ 3 and 0 ≤ y ≤ 9 is 486
b) Evaluating the double integral ∫[-3, 10]∫[-1, -4] 5x dy dx:
∫[-3, 10] 5x(y)|[-4, -1] dx
= ∫[-3, 10] 5x((-1) - (-4)) dx
= ∫[-3, 10] 15x dx
= [15x²/2]|[-3, 10]
= (15(10)²/2) - (15(-3)²/2)
= 750 - 202.5
= 547.5
The value of the double integral is 547.5.
c) To calculate this double integral, we integrate with respect to x first and then with respect to y:
∫[0, 7/3] yx/3 | [0, 3] dy
= ∫[0, 7/3] (3y - 0) dy
= [3y/2] | [0, 7/3]
= (3(7/3)/2) - (3(0)/2)
= (21/2) - 0
= 21/2
= 10.5
The value of the double integral with the order of integrals reversed is 10.5.
Learn more about Double Integral at
brainly.com/question/27360126
#SPJ4
Guys I’m back, this is the other page of the other one

Answers
Therefore, the diameter of the circle is 32 cm, the circumference is approximately 100.53 cm, and the area is approximately 804.25 cm².
What is circle?A circle is a closed two-dimensional figure where all points on the edge of the figure are equidistant from the center point. It is formed by taking a plane and cutting out a circular shape with a constant radius. The distance around the edge of the circle is called the circumference, and the distance from the center to the edge is called the radius. The area enclosed by the circle is calculated as π times the square of the radius.
Here,
1. The diameter of a circle is 10 cm, which means the radius is half of the diameter, or:
r = d/2
= 10/2
= 5 cm
The circumference of a circle is given by the formula:
C = 2πr
where π (pi) is a constant approximately equal to 3.14159. Substituting the value of r, we get:
C = 2π(5)
= 10π
≈ 31.42 cm (rounded to two decimal places)
The area of a circle is given by the formula:
A = πr²
Substituting the value of r, we get:
A = π(5)²
= 25π
≈ 78.54 cm² (rounded to two decimal places)
2. The diameter of a circle with radius 9 mm is 2 times the radius, which is 2 × 9 mm = 18 mm.
The circumference of a circle with radius 9 mm can be found using the formula:
Circumference = 2πr
where π is pi (approximately 3.14) and r is the radius. So, the circumference is:
Circumference = 2 × 3.14 × 9 mm
≈ 56.52 mm
The area of a circle with radius 9 mm can be found using the formula:
Area = πr²
So, the area is:
Area = 3.14 × (9 mm)²
≈ 254.34 mm²
3. The diameter of the circle is:
diameter = 2 × radius
= 2 × 19 cm
= 38 cm
The circumference of the circle is:
circumference = 2 × π × radius
= 2 × π × 19 cm
≈ 119.38 cm
The area of the circle is:
area = π × radius²
= π × 19² cm²
≈ 1134.11 cm²
4. The diameter, circumference and area of a circle with a radius of 2 mm are:
Diameter = 2 x radius
= 2 x 2 mm
= 4 mm
Circumference = 2 x pi x radius
= 2 x 3.14 x 2 mm
= 12.56 mm (rounded to two decimal places)
Area = pi x radius²
= 3.14 x (2 mm)²
= 12.56 mm² (rounded to two decimal places)
5. The radius (r) of the circle is half the diameter (d), so:
r = d/2
= 30 cm / 2
= 15 cm
The circumference (C) of the circle is given by the formula:
C = 2πr
where π (pi) is a mathematical constant approximately equal to 3.14159. So:
C = 2π(15 cm)
= 30π cm
≈ 94.25 cm (rounded to the nearest hundredth)
The area (A) of the circle is given by the formula:
A = πr²
So:
A = π(15 cm)²
= 225π cm²
≈ 706.86 cm²(rounded to the nearest hundredth)
6. The diameter of a circle with a radius of 17 mm is 34 mm (2 times the radius).
The circumference of the circle is given by the formula:
C = 2πr
where r is the radius and π (pi) is a mathematical constant approximately equal to 3.14.
So, the circumference of the circle is:
C = 2π × 17 mm
C ≈ 106.81 mm
The area of the circle is given by the formula:
A = πr²
So, the area of the circle is:
A = π × (17 mm)²
A ≈ 907.92 mm²
7. The radius of the circle is half of the diameter, so the radius is 8 cm / 2 = 4 cm.
The circumference of the circle is given by the formula:
C = 2πr
where r is the radius and π is a mathematical constant approximately equal to 3.14. So, the circumference of the circle is:
C = 2π(4 cm)
= 8π cm
≈ 25.13 cm
The area of the circle is given by the formula:
A = πr²
So, the area of the circle is:
A = π(4 cm)²
= 16π cm²
≈ 50.27 cm²
8. The radius of a circle is half of its diameter. Therefore, if the diameter of a circle is 20 mm, its radius is:
radius = diameter / 2
= 20 mm / 2
= 10 mm
The circumference of a circle can be found using the formula:
circumference = 2 * π * radius
where π (pi) is a mathematical constant approximately equal to 3.14159.
So, the circumference of the circle with a radius of 10 mm is:
circumference = 2 * π * 10 mm
= 20π mm
≈ 62.83 mm
The area of a circle can be found using the formula:
area = π * radius²
So, the area of the circle with a radius of 10 mm is:
area = π * 10 mm²
= 100π mm²
≈ 314.16 mm²
9. The diameter of the circle is 2 times the radius, so:
Diameter = 2 x Radius
= 2 x 16 cm
= 32 cm
The circumference of the circle is given by:
Circumference = 2 x π x Radius
where π is the mathematical constant pi, approximately equal to 3.14.
Circumference = 2 x π x 16 cm
≈ 100.53 cm
The area of the circle is given by:
Area = π x (Radius)²
Area = π x (16 cm)²
≈ 804.25 cm²
To know more about circle,
https://brainly.com/question/26533660
#SPJ1
The probability amplitude ψ(x) for a certain particle to be at position x is:
ψ(x) = sqrt(x) / (a * sqrt(2)) for 0 is less than or equal to x and x is less than or equal to a
1) explain what the quantity |ψ(x)|2 tells us about this particle
2) Calculate the probability that the particles is found between x = 0 and x = a
3) Calculate the probability that the particle is found anywhere else (ie not between x = 0 and x =a)
Answers
1) The quantity |ψ(x)|² tells us the likelihood of finding the particle at a particular position x.
2) The probability of finding the particle between x = 0 and x = a is 1/4 or 25%.
3) The probability of finding the particle outside the range of 0 to a is 3/4 or 75%.
1) The quantity |ψ(x)|², also known as the probability density, tells us the likelihood of finding the particle at a particular position x. It is obtained by taking the absolute square of the probability amplitude ψ(x).
2) To calculate the probability of finding the particle between x = 0 and x = a, we need to integrate the probability density over this interval:
P(0 ≤ x ≤ a) = ∫|ψ(x)|² dx from 0 to a
Plugging in ψ(x) and simplifying, we get:
P(0 ≤ x ≤ a) = ∫(x / (a² * 2)) dx from 0 to a
Evaluating this integral, we obtain:
P(0 ≤ x ≤ a) = (x² / (2 * a² * 2)) | from 0 to a = (a² / (4 * a²)) - (0² / (4 * a²)) = 1/4
So the probability of finding the particle between x = 0 and x = a is 1/4 or 25%.
3) The probability of finding the particle anywhere else, i.e., not between x = 0 and x = a, can be calculated as the complement of the probability of finding it between 0 and a:
P(not between 0 and a) = 1 - P(0 ≤ x ≤ a) = 1 - 1/4 = 3/4
Thus, the probability of finding the particle outside the range of 0 to a is 3/4 or 75%.
To know more about probability, refer to the link below:
https://brainly.com/question/15710566#
#SPJ11
a parallelogram has one angle that measures 40 what are the measures of the other three angles in the parallelogram
Answers
Answer:
40°, 140°, and 140°
Step-by-step explanation:
I need help understanding what I did wrong in my answer. I’m not understanding the answer key answer. Instructions are to factor these trinomial

Answers
See the two pictures, explanation and solution ^_^
In order to check your answer is true or false. We check the two analyzes whether the number from the equation becomes 19x. First you multiply the first number in the first bracket by the second number in the second bracket 2x by 3 to get 6x. Secondly, you multiply the second number of the first bracket by the first number of the second bracket -5 by 4x to get -20x. The sum of the two numbers that you extracted from multiplying the numbers in parentheses (6x) + (-20x) equals - 14x, so this number is not the number 19x, so the first analysis error . Try it for the second analysis .
You can multiply the parentheses together and check the solution too.
\((2x - 5)(4x + 3) \\ (2x)(4x) + (2x)(3) + ( - 5)(4x) + ( - 5)(3) \\ = 8 {x}^{2} + 6x - 20x - 15 \\ = 8 {x}^{2} - 14x - 15\)
\((8x - 5)(x + 3) \\ (8x)(x) + (8x)(3) + ( - 5)(x) + ( - 5)(3) \\ = 8 {x}^{2} + 24x - 5x - 15 \\ = 8 {x}^{2} + 19x - 15\)


Help me please need ASAP

Answers
Answer:
1
i belive
Step-by-step explanation:
the distribution of the number of siblings of students at a local high school has a mean of 2.2 siblings, a standard deviation of 1.4 siblings, and is strongly skewed right. suppose we select a random sample of size 50 from the students at the high school. what is the approximate probability that the mean number of siblings in the sample of size 50 is at most 2?
Answers
The approximate probability that the mean number of siblings in the sample of size 50 is at most 2 is 0.1562 or 15.62%.
What is probability?
Probability is a measure of the likelihood of an event occurring. It is a number between 0 and 1, where 0 means the event is impossible and 1 means the event is certain to happen.
To answer this question, we need to use the central limit theorem, which states that the sample mean of a large enough sample from any population with a finite mean and variance will follow a normal distribution with a mean equal to the population mean and a standard deviation equal to the population standard deviation divided by the square root of the sample size.
In this case, we have a sample size of 50, which is considered large enough for the central limit theorem to apply. Therefore, the mean of the sample means will be equal to the population mean, which is 2.2, and the standard deviation of the sample means will be equal to the population standard deviation divided by the square root of the sample size, which is 1.4/sqrt(50) = 0.198.
To find the probability that the mean number of siblings in the sample of size 50 is at most 2, we need to calculate the z-score and use the standard normal distribution table or calculator. The z-score can be calculated as:
z = (2 - 2.2) / 0.198 = -1.01
Using the standard normal distribution table or calculator, we can find that the probability of getting a z-score of -1.01 or less is approximately 0.1562.
Therefore, the approximate probability that the mean number of siblings in the sample of size 50 is at most 2 is 0.1562 or 15.62%.
To learn more about probability from the given link:
https://brainly.com/question/30034780
#SPJ4
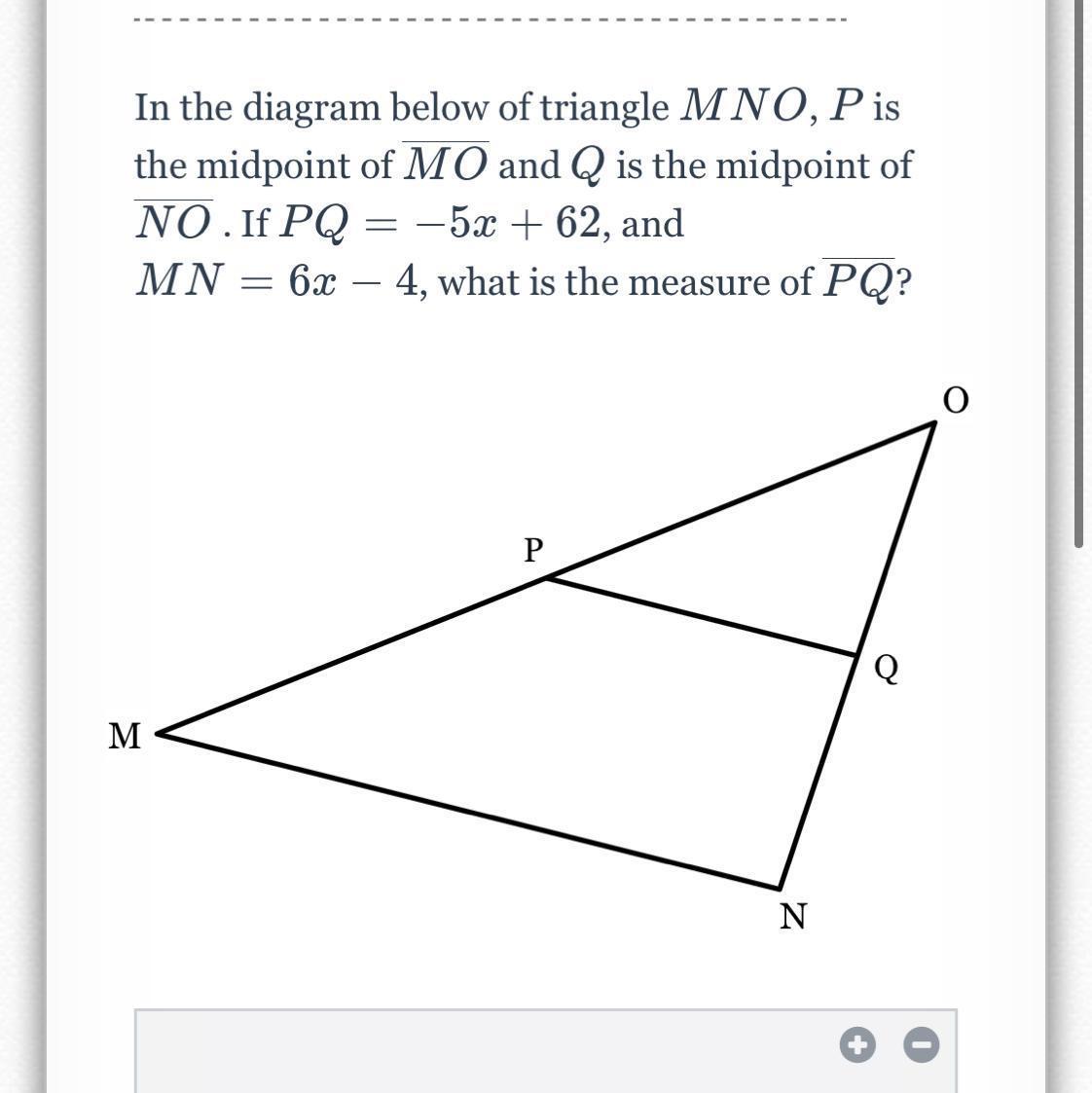
In the diagram below of triangle MNOP, P is the midpoint of MO and Q is the midpoint of NO. If PQ=5x+62 and MN=6x-4, what is the measure of PQ
Answers
The measure of length PQ will be 22 units.
What is the mid-point theorem?A triangle's third side is stated to be parallel to the line segment uniting its two midpoints, and it is also half as long as the third side.
Given:
PQ = 5x + 62, and MN = 6x-4
Now, using Mid- Point Theorem
PQ= 1/2 MN
-5x+ 62 = 1/2( 6x - 4)
-5x+ 62 = 3x - 2
-5x- 3x = -2 - 62
-8x = -64
x= 8
PQ= 5x+ 62 = -5(8) + 62 = -40 + 62 = 22
Hence, the measure of PQ is 22 units.
The missing image is attached below.
Learn more about the midpoint theorem here:
brainly.com/question/13677972
#SPJ1
need help it is math

Answers
Answer:
what do u need my guy 0899
Answer:
The mean is 82.727272727273 rounded 83
Step-by-step explanation:
You add all the numbers:
40 + 75 + 80 + 80+ 81 + 84 + 88 + 90 + 92 + 100 + 100= 910
You divide that result by the total of numbers to add, in this case 11
910/11= 82.727272727273
To round any number, consider that if it is 5 or above it you can round it to the nearest hundred.
Just in case
MODE: 100, 80
MEDIAN: 84
What is a fraction form of $1.80?
Answers
Answer:Okay, so the first thing to do here is show you that any number can be a fraction if you use a 1 as the denominator. Take a look:
1.80
1
What we really want to do though, is get rid of the decimal places completely so that the numerator in our fraction is a whole number. To do this, we have to count the numbers after the decimal point, which in this case is 80.
To get a whole fraction we need to multiply both the numerator and the denominator by 10 if there is one number after the decimal point, 100 if there are two numbers, 1,000 if it's three numbers and 10,000 if it's...well, you get the idea!
In our case 80 is 2 digits long so we need to multiply the numerator and denominator by 100.
Now we just need to do that multiplication to get our whole fraction:
1.80 x 100
1 x 100
=
180
100
The next step is to simplify this fraction and, to do that, we need to find the greatest common factor (GCF). This is sometimes also known as:
Greatest Common Divisor (GCD)
Highest Common Factor (HCF)
Greatest Common Denominator (GCD)
The GCF can be a bit complicated to work out by hand but you can use our handy GCF calculator to figure it out.
In the case of 180 and 100, the greatest common divisor is 20. This means that to simplify the fraction we can divide by the numerator and the denominator by 20 and we get:
180/20
100/20
=
9
5
And there you have it! In just a few short steps we have figured out what 1.80 is as a fraction. The complete answer for your enjoyment is below:
1 4/5
Note: because 180 is greater than 100 we have simplified this fraction even further to a mixed fraction.
Step-by-step explanation: