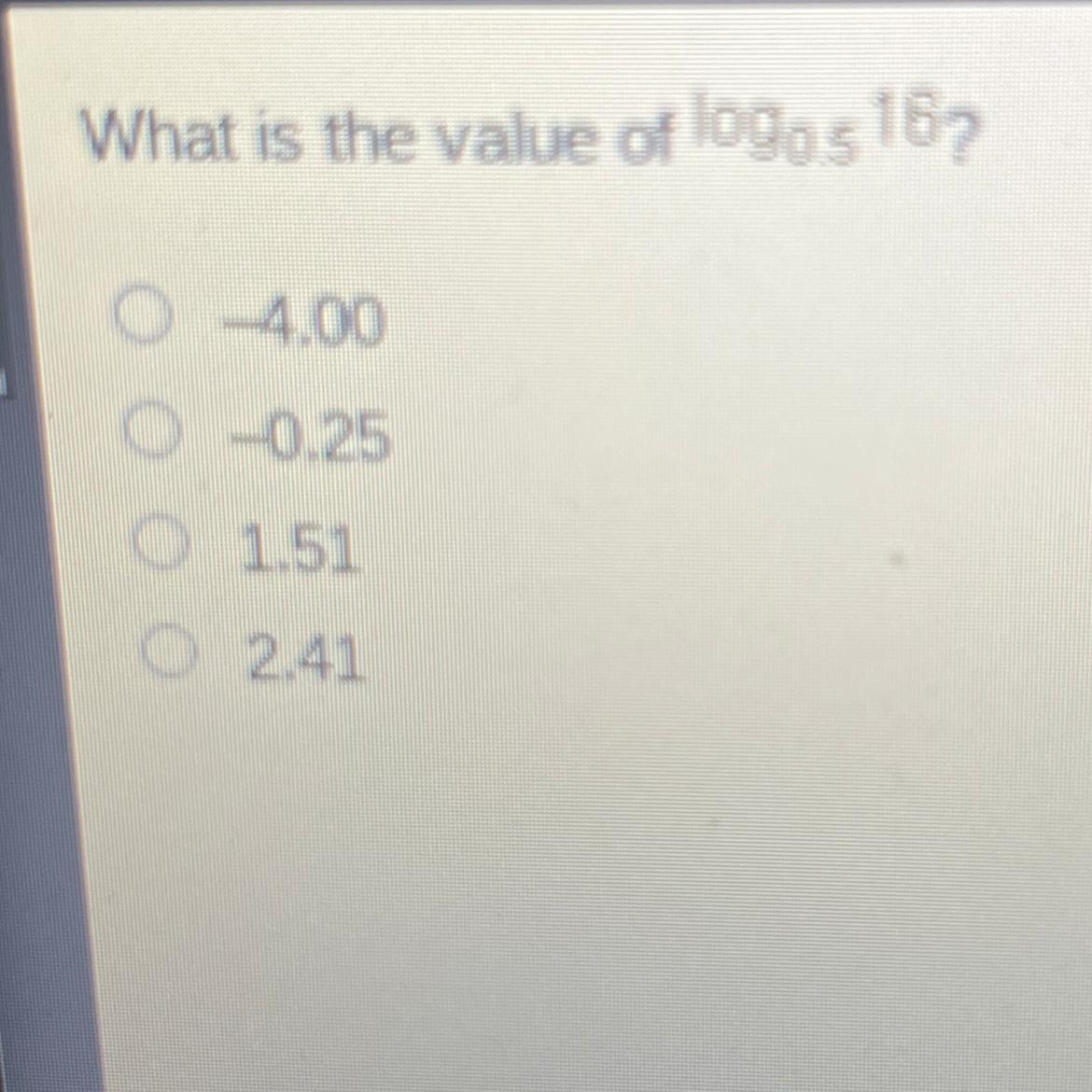Help please need help

The "d" format specifier is used to denote a signed decimal integer in various programming languages and formatting systems.

When used in format strings or printf-style functions, the "d" specifier indicates that the corresponding argument should be formatted as a signed decimal integer. It allows for the representation of both positive and negative whole numbers, including zero.

For example, in C programming, the printf function can be used with the "%d" format specifier to display a signed decimal integer value. Similarly, in other languages such as Python, the "{:d}" format specifier can be used with the format() function or string interpolation to represent a signed decimal integer.

Using the "d" specifier ensures that the output is formatted as a base-10 representation of a signed integer, taking into account the sign of the number.

To know more about "d" format specifier refer here:

https://brainly.com/question/10665222#

#SPJ11

Point A (1, 0) and point B (3/5, 4/5) both lie on the unit circle with center at the origin.

A circle is a geometric shape defined as the set of all points in a plane that are equidistant from a fixed point called the center. The distance between any point on the circle and the center is called the radius.

Center: The center is a fixed point in the plane from which all points on the circle are equidistant. It is denoted by the coordinates (h, k), where h represents the x-coordinate and k represents the y-coordinate of the center.

Radius: The radius is the distance between the center of the circle and any point on the circle. It is denoted by the letter "r". The radius is constant for all points on the circle.

Diameter: The diameter is a line segment passing through the center of the circle and with endpoints on the circle. It is twice the length of the radius, and it divides the circle into two equal halves.

In the xy-plane, the unit circle with center at the origin (0, 0) is defined by all the points that are at a distance of 1 unit from the origin.

Point A: (1, 0)

Point A lies on the x-axis and is 1 unit away from the origin. It represents a point on the unit circle.

Point B: (3/5, 4/5)

Point B lies on the unit circle but is not one of the standard points (such as (1, 0), (-1, 0), (0, 1), or (0, -1)). Instead, it represents a point on the unit circle with coordinates (3/5, 4/5). The x-coordinate of B is 3/5, and the y-coordinate is 4/5. The distance between point B and the origin (0, 0) is 1 unit, which satisfies the condition of being on the unit circle.

Therefore, point A (1, 0) and point B (3/5, 4/5) both lie on the unit circle with center at the origin.

To know more about radius visit:

https://brainly.com/question/31831831

#SPJ11

It will take 62.91 years for Kevin to make the amount  $2500 to  $7500 .

In the question ,

it is given that ,

the amount that Kevin deposited (P) in bank = $2500

the interest rate (r) = 1.75% ,

the compound interest is quarterly ,

So , n is = 4 .

let the time taken to earn $7500 be = x years ;

Substituting the values in the Amount formula for the Compound Interest ,

Amount = P(1 + r/n)ⁿˣ

7500 = 2500(1 + 0.0175/4\()^{4x}\)

Simplifying further ,

we get ,

3 = (1.004375\()^{4x}\)

After applying log both the sides ,

we get ,

log(3) = 4x*log(1.004375)

x = log(3)/(4*log(1.004375))

Simplifying further ,

we have ,

x = 62.91 years .

Therefore , the time taken is = 62.91 years

Learn more about Compound Interest here

https://brainly.com/question/29453448

#SPJ4

Answer:

.35/100

Step-by-step explanation:

35 cents over 1.00

Answer:

7/20 is the simplest form

Step-by-step explanation:

The product of the three consecutive even numbers i.e. 16,18,20 is 5760.

Part A: To find the product of three consecutive even numbers whose sum is 54.

Part B: Let's represent the first even number as x. Since the numbers are consecutive, the second even number would be x + 2, and the third even number would be x + 4.

Now we can set up an equation based on the given information:

x + (x + 2) + (x + 4) = 54

Simplifying the equation, we get:

3x + 6 = 54

Subtracting 6 from both sides:

3x = 48

Dividing both sides by 3:

x = 16

So the first even number is 16, the second even number is 16 + 2 = 18, and the third even number is 16 + 4 = 20.

To find the product of these three numbers:

Product = 16 × 18 × 20 = 5760

To learn more about consecutive even numbers click here:

brainly.com/question/28919582

#SPJ11

The result should be interpreted with caution and cannot be directly extrapolated to the real-world Fender's blue butterfly populations, and the simulation does not take these factors into account.

The result of the simulation suggests that in a hypothetical scenario where the Fender's blue butterfly population is restricted to stepping stones, and the leave prairie probability is set to 0.9, the population is likely to increase over time. However, it is important to note that the simulation represents an idealized scenario and may not reflect the complexity of real-world butterfly populations.

Furthermore, the absence of fires in the simulation may not reflect the natural habitat of Fender's blue butterfly, as fire is a crucial factor in maintaining prairie habitats. In the real world, fire suppression and habitat fragmentation are major threats to the survival of Fender's blue butterfly populations, and the simulation does not take these factors into account.

In summary, while the simulation result may provide insights into the potential effectiveness of using stepping stones to conserve butterfly populations, it should be interpreted with caution and cannot be directly extrapolated to the real-world Fender's blue butterfly population. Further research and monitoring of butterfly populations in their natural habitats are necessary to fully understand their dynamics and inform conservation efforts.

Learn more about population

brainly.com/question/25630111

#SPJ11

2.5 cm, 6.5 cm, and 6 cm are the sides of a right triangle.

The sides of a triangle are 2.5 cm, 6.5 cm, and 6 cm in length.

The Pythagorean Theorem states that The sum of the squares representing the base and height equals the square of the hypotenuse.

\((Perpendicular)^{2}+(Base)^{2}=(Hypotenuse)^{2}\)

                        \((2.5)^{2}+(6)^{2}=(6.5)^{2}\)

                            6.25 + 36 = 42.25

                                  42.25 = 42.25

The sides offered satisfy the specifications for a right triangle.

Given that it satisfies the Pythagorean theorem, a right triangle with sides of 2.5 cm, 6.5 cm, and 6 cm can be built.

Hence, 2.5 cm 6.5 cm 6 cm can be the sides of a right triangle.

To learn more about triangle here:

https://brainly.com/question/2773823

#SPJ4

Answer:

20x

Step-by-step explanation:

Answer:

\(perimeter = 2(l + w) \\ = 2((4x + 2) + 2) \\ = 2(4x + 4) \\ =( 8x + 8) \: units \\ \\ area = l \times w \\ = (4x + 2) \times 2 \\ = (8x + 4) \: sq \: units\)

Answer:

((n-2)*180)/n

Where,

n= the number of of sides in the polygon.

The equation that shows an example of the associative property of addition is:

\(\((-7+i)+7i = -7 + (i+7i)\)\)

According to the associative property of addition, the grouping of numbers being added does not affect the result. In this equation, we can see that both sides of the equation represent the addition of three terms:

\(\((-7+i)\), \(7i\),\)  and  \(\(i\).\)  The equation shows that we can group the terms in different ways without changing the sum.

The equation  \(\((-7+i)+7i = -7 + (i+7i)\)\)  demonstrates the associative property by grouping  \(\((-7+i)\)\) and  \(\(7i\)\)  together on the left side of the equation, and  \(\(-7\)\) and  \(\((i+7i)\)\)  together on the right side of the equation. Both sides yield the same result, emphasizing the associative nature of addition.

To know more about equation visit-

brainly.com/question/9970716

#SPJ11\(\((-7+i)+7i = -7 + (i+7i)\)\)

The expected value in a binomial situation with n = 18 and π = 0.60 is E(X) = np = 18 * 0.60 = 10.8.

In a binomial situation, the expected value, denoted as E(X), represents the average or mean outcome of a random variable X. It is calculated by multiplying the number of trials, denoted as n, by the probability of success for each trial, denoted as π.

In this case, we are given n = 18 and π = 0.60. To find the expected value, we multiply the number of trials, 18, by the probability of success, 0.60.

n = 18 (number of trials)

π = 0.60 (probability of success for each trial)

To find the expected value:

E(X) = np

Substitute the given values:

E(X) = 18 * 0.60

Calculate the expected value:

E(X) = 10.8

learn more about binomial here:

https://brainly.com/question/31049218

#SPJ4

Answer:

\(6b\)

Step-by-step explanation:

We know that the distance formula is \(\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}\). We already have the x values, which are \(5a\) and \(-a\), subtracting \(-a\) from 5a gets us \(6a\).

Same concept for the y values, let's subtract the first y value from the second.

The second y value is \(b\), while the first is \(-5b\)

\(b - (-5b) = b + 5b = 6b\)

Hope this helped!

Answer:

6b is your answer!

Step-by-step explanation:

I wish ALL ACELLUS USERS LUCK

Answer:

We conclude that:

Step-by-step explanation:

Given the function

\(f(x) = 11 - 6(x - 8)\)

Important Tip:

substitute x = -3 in the equation

\(f(x) = 11 - 6(x - 8)\)

\(f(-3) = 11 - 6(-3 - 8)\)

\(f\left(-3\right)\:=\:11-\left(-66\right)\)

\(f\left(-3\right)\:=\:11+66\)               ∵ Apply rule  -(-a) = a

\(f\left(-3\right)=77\)

Therefore, we conclude that:

Answer:

y = - 9x + 14

Step-by-step explanation:

the equation of a line in slope- intercept form is

y = mx + c ( m is the slope and c the y- intercept )

calculate m using the slope formula

m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)

with (x₁, y₁ ) = (- 4, 50 ) and (x₂, y₂ ) = (5, - 31 )

m = \(\frac{-31-50}{5-(-4)}\) = \(\frac{-81}{5+4}\) = \(\frac{-81}{9}\) = - 9 , then

y = - 9x + c ← is the partial equation

to find c substitute either of the 2 points into the partial equation

using (5, - 31 )

- 31 = - 9(5) + c = - 45 + c ( add 45 to both sides )

14 = c

y = - 9x + 14 ← equation of line

The coordinates of the rectangle are (3,-3), (3, -7), (7, -7) and (7, -3).

We also know that the distance between the left and right sides of the rectangle is 4 (since the x-coordinate of the right side is 7 and the x-coordinate of the left side is 3). So we have the equation:

4x = 16

Solving for x, we get x = 4. This means that the length of the top and bottom sides of the rectangle is 4 units. The height of the rectangle is 16/4 = 4 units.

Now that we know the length and height of the rectangle, we can draw it on the coordinate plane.

The left side starts at (3, -3) and ends at (3, -7). The right side starts at (7, -3) and ends at (7, -7).

The top side starts at (3, -3) and ends at (7, -3). The bottom side starts at (3, -7) and ends at (7, -7).

To know more about rectangle here

https://brainly.com/question/8663941

#SPJ1

The sequence of transformations that will map figure H onto figure H' is: Option B:  the rotation of 180° about the origin, translation of (x + 10, y − 2), and reflection across y = −6.

We are given the coordinates of the hexagon as:

Points of Hexagon H  →  (2,2), (2,6), (6,7), (8,6), (8,2), (6,1)

Points of Hexagon H' →  (2,-8), (2,-4), (4,-3), (8,-4), (8,-8), (4,-9)

The steps that can be used to transform the hexagon H into hexagon H' are:

Step 1 - Translate the hexagon in the positive x-axis direction by a factor of 10.

Step 2 - Translate the graph obtained in the above step by factor 2 in the downward direction.

Step 3 - Rotate the graph obtained in the above step 180 degrees about the origin.

Step 4 - Then take the reflection of the graph obtained in the above step about y = -6. The resulting graph shows the graph of Hexagon H'.

Read more about Sequence of Transformation at: https://brainly.com/question/4289712

#SPJ1

Answer:

Step-by-step explanation:

Flour : sugar : butter

= 6 : 2 : 3

butter = 3 part = 180 g

sugar = 2 part = 180×2/3 = 120 g

flour = 6 part = 180×6/3 = 360 g

Answer:

3 meters per second.

Step-by-step explanation:

The formula for finding speed is: \(s = \frac{d}{t}\). D is distance. T is time. So in your case, you would divide 6.0 (distance) by 2.0 (time). Your answer is 3. Add meters per second because you divided meters/seconds.

Hope it helps!

Answer: -19.2

Step-by-step explanation:

If the diameter of a circle is 6 units, it's radius would be half that, that is 3 units.

Circumference = \(2\pi r\) = 2 x 3.14 x 3 = 18.84 units

Answer:

y = 90 and z = 62.........

False. A rectangle is conventionally used in a process flowchart to represent a storage area or queue. Triangles are typically used in flowcharts to represent decision points, where a choice must be made between two or more alternatives.

Rectangles are used to represent activities or operations, while arrows connecting the shapes indicate the flow or direction of the process. The use of standardized shapes in flowcharts helps to make them easily understandable and accessible to a wide range of individuals, regardless of their background or experience with the specific process being depicted.

To learn more about rectangle : brainly.com/question/15019502

#SPJ11

Answer:

I do not know I am very sorry brother now begone

Answer:

given: 300km in 6 hours

formula: a÷b=x

work: 300÷6=x

          50= x

answer: the avrage

speed of the car is 50km an hour

Step-by-step explanation:

The x-intercept of line A is (1,0) and the x - intercept of line B is (-2,0).

Given:

Equation of Line A: y-2=-(x+1)

on finding x intercept put y = 0

0 - 2 = -x - 1

-2 = -x - 1

-x = -2 + 1

-x = -1

x = 1.

The x intercept is (1,0)

The x intercept for the line B is (-2,0).

Therefore the x-intercept of line A is (1,0) and the x - intercept of line B is (-2,0).

Learn more about the x intercept here:

https://brainly.com/question/14180189

#SPJ1

The maximum value of z is 0, and the values of the decision variables are x1 = 0, x2 = 10, x3 = 0, x4 = 0.

maximize: z = c1x1 + c2x2 + ... + cnxn

subject to

a11x1 + a12x2 + ... + a1nxn ≤ b1

a21x1 + a22x2 + ... + a2nxn ≤ b2

am1x1 + am2x2 + ... + amnxn ≤ bmxi ≥ 0 for all i

In our case,

the given LP is:maximize: z = 36x1 + 30x2 - 3x3 - 4x

subject to:

x1 + x2 - x3 ≤ 5

6x1 + 5x2 - x4 ≤ 10

xi ≥ 0 for all i

We can rewrite the constraints as follows:

x1 + x2 - x3 + x5 = 5  (adding slack variable x5)

6x1 + 5x2 - x4 + x6 = 10  (adding slack variable x6)

Now, we introduce the non-negative variables x7, x8, x9, and x10 for the four decision variables:

x1 = x7

x2 = x8

x3 = x9

x4 = x10

The objective function becomes:

z = 36x7 + 30x8 - 3x9 - 4x10

Now we have the problem in standard form as:

maximize: z = 36x7 + 30x8 - 3x9 - 4x10

subject to:

x7 + x8 - x9 + x5 = 5

6x7 + 5x8 - x10 + x6 = 10

xi ≥ 0 for all i

To apply the simplex algorithm, we initialize the simplex tableau as follows:

  |  Cj   |   x5   |   x6   |   x7   |   x8   |   x9   |   x10  |    RHS  |

---------------------------------------------------------------------------

z |  0    |   0    |   0    |  36    |   30   |   -3   |   -4   |    0    |

---------------------------------------------------------------------------

x5|   0   |   1    |   0    |   1    |   1    |   -1   |   0    |    5    |

---------------------------------------------------------------------------

x6|   0   |   0    |   1    |   6    |   5    |   0    |   -1   |   10    |

---------------------------------------------------------------------------

Now, we can proceed with the simplex algorithm to find the optimal solution. I'll perform the iterations step by step:

Iteration 1:

1. Choose the most negative coefficient in the 'z' row, which is -4.

2. Choose the pivot column as 'x10' (corresponding to the most negative coefficient).

3. Calculate the ratios (RHS / pivot column coefficient) to find the pivot row. We select the row with the smallest non-negative ratio.

Ratios: 5/0 = undefined, 10/(-4) = -2.5

4. Pivot at the intersection of the pivot row and column. Divide the pivot row by the pivot element to make the pivot element 1.

5. Perform row operations to

make all other elements in the pivot column zero.

After performing these steps, we get the updated simplex tableau:

  |  Cj   |   x5   |   x6   |   x7   |   x8   |   x9   |   x10  |    RHS  |

---------------------------------------------------------------------------

z |  0    |   0    |  0.4   |  36    |   30   |   -3   |   0    |   12    |

---------------------------------------------------------------------------

x5|   0   |   1    |  -0.2  |   1    |   1    |   -1   |   0    |   5     |

---------------------------------------------------------------------------

x10|   0  |   0    |   0.2  |   1.2  |   1   |   0    |   1    |   2.5   |

---------------------------------------------------------------------------

Iteration 2:

1. Choose the most negative coefficient in the 'z' row, which is -3.

2. Choose the pivot column as 'x9' (corresponding to the most negative coefficient).

3. Calculate the ratios (RHS / pivot column coefficient) to find the pivot row. We select the row with the smallest non-negative ratio.

Ratios: 12/(-3) = -4, 5/(-0.2) = -25, 2.5/0.2 = 12.5

4. Pivot at the intersection of the pivot row and column. Divide the pivot row by the pivot element to make the pivot element 1.

5. Perform row operations to make all other elements in the pivot column zero.

After performing these steps, we get the updated simplex tableau:

  |  Cj   |   x5   |   x6   |   x7   |   x8   |   x9   |   x10  |    RHS  |

---------------------------------------------------------------------------

z |  0    |   0    |  0.8   |  34    |   30   |   0    |   4    |   0     |

---------------------------------------------------------------------------

x5|   0   |   1    |  -0.4  |   0.6  |   1    |   5   |   -2   |   10    |

---------------------------------------------------------------------------

x9|   0   |   0    |   1    |   6    |   5    |   0   |   -5   |   12.5  |

---------------------------------------------------------------------------

Iteration 3:

No negative coefficients in the 'z' row, so the optimal solution has been reached.The optimal solution is:

z = 0

x1 = x7 = 0

x2 = x8 = 10

x3 = x9 = 0

x4 = x10 = 0

x5 = 10

x6 = 0

Therefore, the maximum value of z is 0, and the values of the decision variables are x1 = 0, x2 = 10, x3 = 0, x4 = 0.

Learn more about Simplex Algorithm here:

https://brainly.in/question/46895640

#SPJ11

The evidence supports the claim that the average life of electric light bulbs is greater than 2000 hours.

a. Null Hypothesis: The average life of electric light bulbs is not greater than 2000 hours. Alternative Hypothesis: The average life of electric light bulbs is greater than 2000 hours.

b. The critical value for a one-tailed test at the 2% level of significance with 63 degrees of freedom is 2.33.

c. The relevant test statistic is:
t = (x - μ) / (s / √n)=\(= \frac{(2008 - 2000)}{\frac{12.31}{\sqrt{64}}}= 13.03\)
Since the test statistic is greater than the critical value of 2.33, we can reject the null hypothesis and conclude that there is sufficient evidence to support the claim.

d. The p-value is the probability of obtaining a test statistic as extreme or more extreme than the observed value, assuming the null hypothesis is true. Using a t-distribution table with 63 degrees of freedom, the p-value is less than 0.01. Since the p-value is less than the significance level of 0.02, we can reject the null hypothesis.

e. Yes, we reject the null hypothesis.

f. No, we do not reject the claim. The evidence supports the claim that the average life of electric light bulbs is greater than 2000 hours.

To know more about hypothesis testing visit:

https://brainly.com/question/28920252

#SPJ11