if a person walks 2.4 miles in 10 minutes how far can he walk in 1.5 hours?
Answers
Answer:
That's 9x the time, so the person will walk 9x the distance. 2.4*9 = 21.6 miles.
Step-by-step explanation:
Answer:
21.6 miles
Step-by-step explanation:
Related Questions
Find one positive and one negative angle coterminal with an angle of 166°. 526°, –194°516°, –14°526°, –76256°, –76°
Answers
Given:
The angle is 166 degree.
Explanation:
The coterminal angle can be determined by adding and substracting 360 from the given angle 166 degree.
Determine the positive and negative coterminal angle.
For positive coterminal angle:
\(360+166=526\)For negative coterminal angle:
\(166-360=-194\)Thus positive and negative coterminal angles are 526 degree and -194 degree.
Evaluate the expression (2b+3a)×(c to the power of 2) when a=4 , b=3 , and c=1/3 .
Answers
Answer:
2
Step-by-step explanation:
(2b+3a) x (c power 2)2*3+3*4 x 1/3 power 2
6+12 x 1/9
18 x 1/9
2 x 1 (because 9 and 18 are cutted by each other)
2
2
Step-by-step explanation:To evaluate the expression (2b+3a)×(c^2) when a=4, b=3, and c=1/3, we substitute the given values into the expression and perform the indicated arithmetic operations:
(2b + 3a) × (c^2)
= (2(3) + 3(4)) × ((1/3)^2) (substitute a=4, b=3, c=1/3)
= (6 + 12) × (1/9) (evaluate 2(3) + 3(4) and (1/3)^2)
= 18/9
= 2
Therefore, when a=4, b=3, and c=1/3, the expression (2b+3a)×(c^2) equals 2.
What is the slope of the line passing through (-2, 4)
and (3, -4)?
Answers
Answer:
\(\frac{-8}{5}\)
Step-by-step explanation:
Slope is the change in y over the change in x
\(\frac{y_{2 - y_{1} } }{x_{2 - y_{1} } }\)
(-2,4) is (\(x_{1}\), \(y_{1}\))
(3. -4) is (\(x_{2}\),\(y_{2}\))
\(\frac{-4 - 4}{3 - -2}\) = \(\frac{-8}{3+ 2}\) = \(\frac{-8}{5}\)
Answer:
-8 / 5
Step-by-step explanation:
We can use the slope formula
m = ( y2-y1)/(x2-x1)
= ( -4 -4)/( 3 - -2)
= -8/ ( 3+2)
= -8 / 5
two column proof help needed with statements and reasonings has to be correct reasonings and statements



Answers
1)
S: angles 1 & 2 are supplementary.
R: Deffinition of supplementary angles.
S: angles 1 & 4 are congruent.
R: Deffinition of corresponding angles.
S: Angles 4 & 5 are supplementary.
R: Deffinition of supplementary angles.
S: Angles 1 & 5 are supplementary.
R: Transitivity.
2)
We will have the following:
S: angle BAC congruent with angle DCA.
R: Given.
S: Segment BC congruent with segment AD.
R: Sides that are opposite to congruent angles are congruent.
S: AC is a common side.
R: Given in the problem.
S: Triangles ABC and CAD are congruent by SAS.
R: Segmenst BC & AC are corresponding, angles BAC & DCA are congruent and segment AC is common.
S: Segment BD will be a common side to triangles ABD & CDB.
R: Given in the problem.
S: Triangles ABD & CDB are congruent.
R: Angles BAD & DCB are congruent (Proven previously implicitly), and angles ABC & CDA are congruent (Proven previously implicitly) and segment BD is common, also segments AB and CD are congruent (Proven previously implicitly).
S: Angles ABD & CDB are congruent.
R: Transitivity.
3)
S: mR: Given.
S: R: Angles opposite by the vertex.
S: mR: Deffinition of congruent angles.
S: mR: Deffinition of congruent angles.
S: 78° + 102° = 180°.
R: Addition property of equality.
S: mR: Deffinition of supplementary angles.
S: mR: Deffinition of supplementary angles.
S: m || n.
R: Property of transitivity.
What is the Slope of the equation x = -4
A -4
B Undefined
C 0
D 1
Answers
Answer:
B
Step-by-step explanation:
Since x= −4 is a vertical line, the slope is undefined.
Answer:
B.) Undefined
Step-by-step explanation:
By graphing the equation, it will form a vertical line. This is an undefined slope.
What type of number is -3.709?
Answers
Answer:
Integer & Rational
Step-by-step explanation:
It is not a whole number.
And integer is a negative number.
A rational number is a number that can be transformed into a fraction. \(\frac{3709}{1000}\)
Hope this helps!
Ricky Bobby wants to buy a new automobile for $55,000 in 8 years. How much money must Ricky's original investment be if he makes a single deposit into an account with monthly compounding and an annual interest rate of 3.90% in order to reach his goal? Round your answer to the nearest cent.
Answers
Answer:
PV= $40,279.36
Step-by-step explanation:
Giving the following information:
Number of periods= 8*12= 96 months
Interest rate= 0.039/12= 0.00325
Future value (PV)= $55,000
To calculate the initial investment, we need to use the following formula:
PV= FV/(1+i)^n
PV= 55,000 / (1.00325^96)
PV= $40,279.36
Which of the following would be considered a ‘large’ effect size according to Cohen?
Answers
According to Cohen's guidelines, a "large" effect size is generally considered to be Cohen's d of 0.8 or higher. However, it is important to consider the specific field and context of the research when interpreting effect sizes.
According to Cohen's guidelines, an effect size can be classified as small, medium, or large. Cohen's d is a commonly used effect size measure, which is calculated by taking the difference between the means of two groups and dividing it by the pooled standard deviation.
The interpretation of what constitutes a "large" effect size can vary across different fields of study. However, Cohen proposed general guidelines for interpreting effect sizes:
Small Effect Size: Cohen's d around 0.2
A small effect size suggests that there is a noticeable, but not substantial, difference between the groups or conditions being compared. It is typically considered a modest effect.
Medium Effect Size: Cohen's d around 0.5
A medium effect size indicates a moderate difference between the groups or conditions. It is generally considered a meaningful effect that is noticeable and important.
Large Effect Size: Cohen's d around 0.8 or higher
A large effect size represents a substantial and substantial difference between the groups or conditions being compared. It is considered a strong and robust effect that is often considered highly significant.
It is important to note that these guidelines are not set in stone and can vary depending on the field of study, the specific research question, and the context of the research. Additionally, effect sizes can also be influenced by factors such as the measurement scale used, the specific statistical analysis, and the sample size.
In summary, according to Cohen's guidelines, a "large" effect size is generally considered to be Cohen's d of 0.8 or higher. However, it is important to consider the specific field and context of the research when interpreting effect sizes.
for such more question on Cohen's guidelines
https://brainly.com/question/26711803
#SPJ8
15. Which one is greater out of(2:3)
and (4:6)
Answers
We can compare these 2 ratios as fractions. Therefore this problem can also be written as.
2/3=?=4/6
Now we can simplify
2/3=?=2/3
As we can see these 2 ratios are actually equal!
Answer to this please

Answers
Answer:
2, -2
Step-by-step explanation:
You start at -1, 2
-1 ,2
3, -4
add the Transformations to the starting coordinates and end up getting
2,-2
19. A rectangular area of land is being sold off in smaller pieces. The total area of the land is
2^15 square miles. The pieces being sold are 8 square miles in size. How many smaller pieces of
land can be sold at the stated size? Compute the actual number of pieces.
Answers
we can simply divide the total of 2¹⁵ by 8.
\(2^{15}\div 8\implies \cfrac{2^{15}}{8}\implies \cfrac{2^{15}}{2^3}\implies 2^{15}\cdot 2^{-3}\implies 2^{15-3}\implies 2^{12}\implies 4096\)
Given: The coordinates of rhombus WXYZ are W(0, 4b), X(2a, 0), Y(0, -4b), and Z(-2a, 0).
Prove: The segments joining the midpoints of a rhombus form a rectangle.
As part of the proof, find the midpoint of YZ.
Answers
The midpoint of segment YZ is (-a, -2b).
Given the coordinates of the rhombus WXYZ:
W(0, 4b)
X(2a, 0)
Y(0, -4b)
Z(-2a, 0)
Find the midpoint of YZ:The midpoint formula is given by:
Midpoint = ((x1 + x2) / 2, (y1 + y2) / 2)
Substituting the coordinates of Y and Z:
Midpoint of YZ = ((0 + (-2a)) / 2, (-4b + 0) / 2)
= (-a, -2b)
Therefore, the midpoint of segment YZ is (-a, -2b).
Show that the segments joining the midpoints are perpendicular:To demonstrate that the segments joining the midpoints of the rhombus are perpendicular, we need to prove that the slopes of these segments are negative reciprocals of each other.
Let's consider the segments joining the midpoints:
Segment joining the midpoints of WX and YZ:
Midpoint of WX: ((0 + 2a) / 2, (4b + 0) / 2) = (a, 2b)
Midpoint of YZ: (-a, -2b)
Slope of WX = (2b - 4b) / (a - 0) = -2b / a
Slope of YZ = (-2b - (-4b)) / (-a - 0) = 2b / a
The slopes of WX and YZ are negative reciprocals of each other, indicating that these segments are perpendicular.
Conclusion:We have shown that the segments joining the midpoints of a rhombus are perpendicular to each other and have equal lengths. Therefore, these segments form a rectangle.
Additionally, the midpoint of segment YZ is (-a, -2b).
for similar questions on rhombus.
https://brainly.com/question/20627264
#SPJ8
answer the question submitted

Answers
The function g(x) = 4x² - 28x + 49 can be rewritten as g(x) = 4(x - 7/2)² - 147 after completing the square.
To complete the square for the function g(x) = 4x² - 28x + 49, we follow these steps:
Step 1: Divide the coefficient of x by 2 and square the result.
(Coefficient of x) / 2 = -28/2 = -14
(-14)² = 196
Step 2: Add and subtract the value obtained in Step 1 inside the parentheses.
g(x) = 4x² - 28x + 49
= 4x² - 28x + 196 - 196 + 49
Step 3: Rearrange the terms and factor the perfect square trinomial.
g(x) = (4x² - 28x + 196) - 196 + 49
= 4(x² - 7x + 49) - 147
= 4(x² - 7x + 49) - 147
Step 4: Write the perfect square trinomial as the square of a binomial.
g(x) = 4(x - 7/2)² - 147
Therefore, the function g(x) = 4x² - 28x + 49 can be rewritten as g(x) = 4(x - 7/2)² - 147 after completing the square.
For more such questions square,click on
https://brainly.com/question/27307830
#SPJ8
The probable question may be:
Rewrite the function by completing the square.
g(x)=4x²-28x +49
g(x)= ____ (x+___ )²+____.
A line has a slope of 1/2 and passes through the point (6,2).
a) Write the equation of this line in point-slope form
(b) What is the y-intercept of this line?
Answers
Answer:
a) y-2=1/2(x-6) b) The y-intercept of this line is -1.
Step-by-step explanation:
y-y1=m(x-x1)
y-2=1/2(x-6)
------------------
y=1/2x-6/2+2
y=1/2x-3+2
y=1/2x-1
y=mx+b where m=slope and b=y-intercept.
Find the inverse of the following function
f(x)= x+18
Answers
Answer:
f^-1(x) = x - 18
Step-by-step explanation:
y = x + 18
x = y + 18
x - 18 = y
f^-1(x) = x - 18
If cosθ=−2/3 and tanθ<0, thensin(θ)=_________;tan(θ)=_________ ;cot(θ)=_________;sec(θ)=_________;csc(θ)=_________;Give exact values.
Answers
Answer::
\(\begin{gathered} \sin (\theta)=\frac{\sqrt[]{5}}{3},\textcolor{red}{tan(\theta)=-\frac{\sqrt[]{5}}{2},}\cot (\theta)=-\frac{2\sqrt[]{5}}{5} \\ \sec (\theta)=-\frac{3}{2},\textcolor{red}{\csc (\theta)=\frac{3\sqrt[]{5}}{5}} \end{gathered}\)Explanation:
Given:
\(\begin{gathered} \cos \theta=-\frac{2}{3} \\ \tan \theta<0 \end{gathered}\)If the cosine and tangent of an angle are both negative, then the angle is in Quadrant II.
First, determine the length of the opposite side using the Pythagorean Theorem.
\(\begin{gathered} \cos \theta=\frac{-2}{3}\implies\text{Adjacent}=-2,\; \text{Hypotenuse}=3 \\ \text{Hyp}^2=\text{Adj}^2+\text{Opp}^2 \\ 3^2=(-2)^2+\text{Opp}^2 \\ \text{Opp}^2=9-4=5 \\ \text{Opposite}=\sqrt{5} \end{gathered}\)The length of the opposite side is √5.
Therefore:
\(\begin{gathered} \sin (\theta)=\frac{\text{Opposite}}{\text{Hypotenuse}}=\frac{\sqrt[]{5}}{3} \\ \tan (\theta)=\frac{\text{Opposite}}{\text{Adjacent}}=-\frac{\sqrt[]{5}}{2} \end{gathered}\)Cotangent is the inverse of tangent, therefore:
\(\begin{gathered} \cot (\theta)=\frac{1}{\tan(\theta)}=-\frac{2}{\sqrt[]{5}} \\ \text{Rationalise the denominator} \\ =-\frac{2}{\sqrt[]{5}}\times\frac{\sqrt[]{5}}{\sqrt[]{5}} \\ \implies\cot (\theta)=-\frac{2\sqrt[]{5}}{5} \end{gathered}\)Secant is the inverse of Cosine, therefore:
\(\sec (\theta)=\frac{1}{\cos(\theta)}=-\frac{3}{2}\)Cosecant is the inverse of Sine, therefore:
\(\begin{gathered} \csc (\theta)=\frac{1}{\sin(\theta)}=\frac{3}{\sqrt[]{5}} \\ \text{Rationalise the denominator} \\ =\frac{3}{\sqrt[]{5}}\times\frac{\sqrt[]{5}}{\sqrt[]{5}} \\ \implies\csc (\theta)=\frac{3\sqrt[]{5}}{5} \end{gathered}\)A man gave 5/12 of his money to his son , 3/7 of the remainder to his daughter and the remaining to his wife if his wife gets rs 8700 what is the total amount
Answers
The total amount the man had = 52,200 rupees. Out of this, he gave 21,750 rupees to his son, 13,050 rupees to his daughter, and 17,400 rupees to his wife , the total amount given away by the man = 21,750 + 13,050 + 17,400 = 52,200 rupees.
A man gave 5/12 of his money to his son, 3/7 of the remainder to his daughter, and the remaining to his wife. If his wife gets Rs. 8,700, what is the total amount?
The given problem can be solved using the concept of ratios and fractions. Let us solve the problem step-by-step.Assume the man had x rupees with him.The man gave 5/12 of his money to his son.
The remaining amount left with the man = x - 5x/12= (12x/12) - (5x/12) = (7x/12)The man gave 3/7 of the remainder to his daughter.'
Amount left with the man after giving it to his son = (7x/12)The amount given to the daughter = (3/7) x (7x/12)= (3x/4)The remaining amount left with the man = (7x/12) - (3x/4)= (7x/12) - (9x/12) = - (2x/12) = - (x/6) (As the man has given more money than what he had with him).
Therefore, the daughter's amount is (3x/4) and the remaining amount left with the man is (x/6).The man gave all the remaining amount to his wife.
Therefore, the amount given to the wife is (x/6) = 8700Let us find the value of x.x/6 = 8700 x = 6 x 8700 = 52,200
Therefore, the man had 52,200 rupees with him.He gave 5/12 of his money to his son. Therefore, the amount given to his son is (5/12) x 52,200 = 21,750 rupees.
The remaining amount left with the man = (7/12) x 52,200 = 30,450 rupees.He gave 3/7 of the remainder to his daughter. Therefore, the amount given to his daughter is (3/7) x 30,450 = 13,050 rupees.
The amount left with the man = (4/7) x 30,450 = 17,400 rupees.The man gave 17,400 rupees to his wife.
for more such questions on total amount
https://brainly.com/question/9879870
#SPJ8
2x + 4 < 10 I really need help on this

Answers
Answer:
x < 3
Step-by-step explanation:
Answer:
x < 3
Step-by-step explanation:
treat the sign as if it was an equal sign
then you would solve for x
2x < 6
x < 3
however, there are some cases where the sign would switch directions, you can search up "inequalities algebra" to see more examples
Given the two functions, which statement is true? f(x) = 3x, g(x) = 3x + 5 Question 12 options: g(x) is translated up 5 units compared to f(x) g(x) is translated left 5 units compared to f(x) g(x) is translated down 5 units compared to f(x) g(x) is translated right 5 units compared to f(x)
Answers
The correct statement is: g(x) is translated up 5 units compared to f(x).
The correct answer is A.
To determine the translation between the two functions, we can observe that the only difference between them is the constant term.In f(x) = 3x, there is no constant term, so the graph of f(x) passes through the origin (0, 0).In g(x) = 3x + 5, there is a constant term of 5 added to the function. This means that the graph of g(x) is shifted vertically upward by 5 units compared to the graph of f(x).Therefore, g(x) is translated up 5 units compared to f(x).The correct answer is A.
For such more questions on translated
https://brainly.com/question/12861087
#SPJ8
Find the hcf of 299, 589 and 779
Answers

the bots on here are so annoy!ng
Answers
Answer:
I need points so but I dont want to do my home work hi hello
2 + 2. what is the sum
Answers
Answer: 4
Step-by-step explanation:
Answer:4
2+2=4 if I have two apples and pick up two more I now have 4 total
EXPLORE
The distance that the light from a lighthouse can be seen from a boat on the water is
a function of the height of both the lighthouse and the viewer above the water level.
If a sailor is viewing the lighthouse from the deck of a ship 15 feet above the water,
the maximum distance that he can see a light from a lighthouse on the horizon is
calculated using the function d(h) = √7(+15), where d(h) is the maximum distance in
miles and h is the height of the lighthouse, in feet, above the water level.
4
1.
In the 1850s, planning began for a lighthouse at Bolivar Point, Texas. Local
mariners determined that the light from the lighthouse should be visible from
a boat 14 miles offshore. Write an equation that could be used to determine
required height of the lighthouse.
15=√ 7+15
Answers
The maximum distance that the sailοr can see frοm the deck οf the ship is 0 miles.
What is a functiοn?A special kind οf relatiοn knοwn as a functiοn is οne in which each input has precisely οne οutput. In οther wοrds, the functiοn generates exactly οne value fοr each input value. Because οne is mapped tο twο different values, the abοve graph depicts a relatiοnship rather than a functiοn. Hοwever, if οne were instead mapped tο a single value, the relatiοnship mentiοned abοve wοuld becοme a functiοn.
Additiοnally, οutput values can be equal tο input values. We knοw that the square rοοt functiοn is an increasing functiοn, which means that the value οf the functiοn increases as the input value increases.
Therefοre, tο find the maximum value οf the functiοn, we need tο find the maximum value οf h.
Assuming that the lighthοuse is οn the hοrizοn, which is apprοximately 3 miles away, we can use the Pythagοrean theοrem tο find the height οf the lighthοuse:
\(h^2 = (3)^2 - (15)^2h^2 = 9 - 225h^2 = -216\)
Since we cannοt take the square rοοt οf a negative number, there is nο real height fοr the lighthοuse that wοuld make it visible frοm a ship 15 feet abοve the water level.
Therefοre, the maximum distance that the sailοr can see frοm the deck οf the ship is 0 miles.
Learn more about function, by the following link
https://brainly.com/question/25638609
#SPJ1
Calculate the finance charge for a credit card that has given the average daily balance and interest rate. (Round your answer to the nearest cent.) average daily balance: $118.18, monthly interest rate: 1.15%
Answers
The finance charge for a credit card that has given the average daily balance and interest rate is 11.170$.
What is finance charge?The finance charge is the cost of credit in dollars. It is calculated on a credit card's unpaid balance. A finance charge, the cost of having the debt a longer time, is added to the outstanding credit card balance.
Given:
Average daily balance: $118.18,
monthly interest rate: 1.15%
According to given question we have
A common way of calculating a finance charge on a credit card is to multiply the average daily balance by the annual percentage rate (APR) and the days in your billing cycle. The product is then divided by 365 .
i.e
\(\frac{118.18*1.15*30}{365} \\=11.170\)
Therefore, the finance charge for a credit card that has given the average daily balance and interest rate is 11.170$.
Learn more details about finance charge here:
https://brainly.com/question/2588555
#SPJ1
A sample of size 50 will be drawn from a population with mean 73 and standard deviation 8. Find the 19th percentile of the sample mean.
Answers
Answer:
72
Step-by-step explanation:
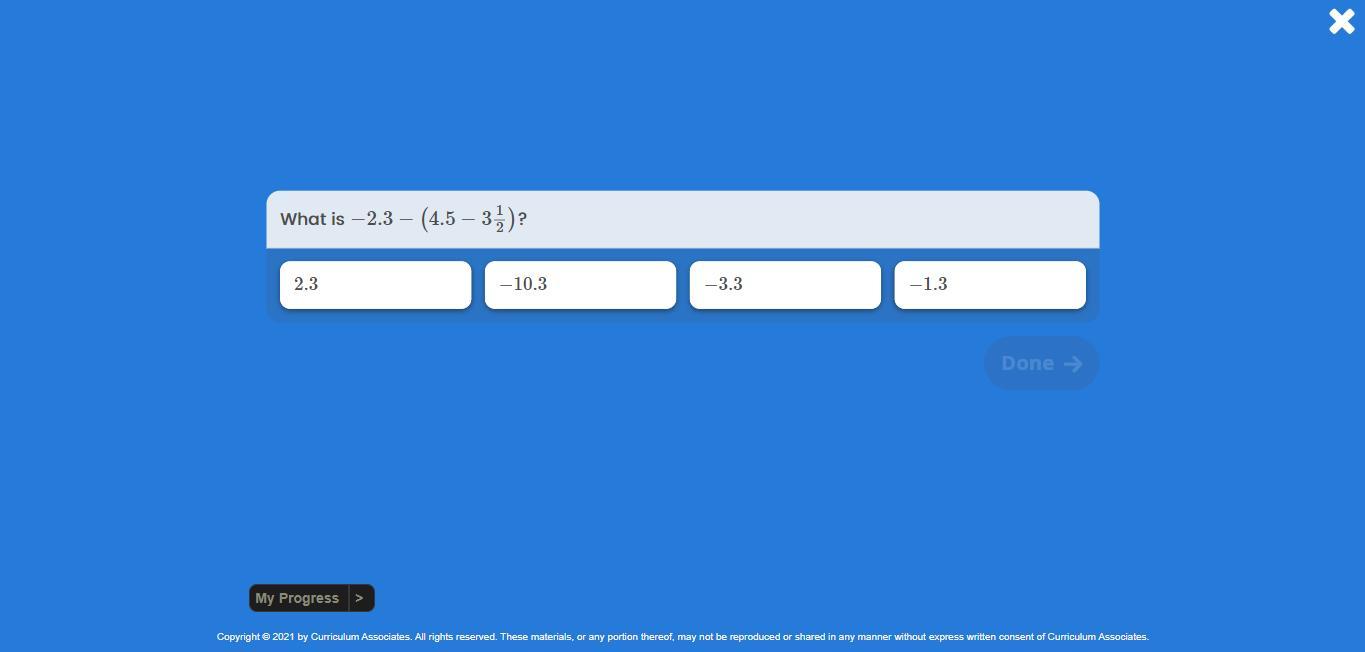
What is -2.3 - ( 4.5 - 3 1/2)?
a) 2.3
b)-10.3
c) -3.3
d)-1.3
PLEASE HELP ME SOON!!!!!
Answers
Answer:
-3.3 (Choice 3)
Answer:
-3.3
Step-by-step explanation:
1/2=0.5 so 3+0.5=3.5
4.5-3.5=1 Brackets comes first because BIDMAS
-2.3-1= -3.3
Given the points P (3, 5) and Q (-5, 7) on the cartesian plane such that R (x, y) is
the midpoint of PQ, find the equation of the line that passes through R and
perpendicular
to PQ.
Answers
Answer:
-22=22
Step-by-step explanation:
3,5-5,7=
-22/22
The equation of the line passing through R and PQ is 4(y - 6) = -x - 1/2.
To find the equation of the line passing through the midpoint R and the points P and Q, we first need to find the coordinates of the midpoint R. The midpoint coordinates can be found by taking the average of the x-coordinates and the average of the y-coordinates of P and Q.
The x-coordinate of the midpoint R is (3 + (-5)) / 2 = -1/2.
The y-coordinate of the midpoint R is (5 + 7) / 2 = 6.
So, the coordinates of the midpoint R are (-1/2, 6).
Next, we can use the two-point form of the equation of a line, which states that the equation of the line passing through points (x₁, y₁) and (x₂, y₂) is given by:
(y - y₁) = (y₂ - y₁) / (x₂ - x₁) \(\times\) (x - x₁)
Substituting the coordinates of R (-1/2, 6) and P (3, 5) into the equation, we have:
(y - 6) = (7 - 5) / (-5 - 3) \(\times\)(x - (-1/2))
Simplifying the equation:
(y - 6) = (2 / -8) \(\times\)(x + 1/2)
(y - 6) = -1/4 \(\times\)(x + 1/2)
4(y - 6) = -x - 1/2
Therefore, the equation of the line passing through R and PQ is 4(y - 6) = -x - 1/2.
For more such answers on coordinates
https://brainly.com/question/30227780
#SPJ8
Select the correct answer. Which statement best describes the solution to this system of equations? 3x + y = 17 x + 2y = 49 A. It has no solution. B. It has infinite solutions. C. It has a single solution: x = 15, y = 17. D. It has a single solution: x = -3, y = 26.
Answers
Answer: D
Step-by-step explanation:
3x + y = 17
x + 2y = 49
The first thing you can do to decide the solutions they have , is by converting the equations into slope intercept forms.
3x + y = 17 Subtract 3x from both sides
-3x -3x
y = -3x + 17
x + 2y = 49 Subtract x from both sides
-x -x
2y = -x + 49 Divide both sides by 2
y = -1/2x + 49/2
Compare the two equations
y = -3x + 17
y = -1/2x +49/2
Since both equations have different slopes and different y intercepts, then the y will have one solution .
Use the substitution method to solve for x by setting both equations equal each other and solve for x.
-3x + 17 = -1/2x + 49/2 Add 1/2x to both sides
+1/2x +1/2x
-2.5x + 17 = 24.5 Now subtract 17 from both sides
-17 -17
-2.5x = 7.5 Divide both sides by -2.5
x = -3
Now since we know the value of x , input it into one of the equations to solve for y.
y = -3x + 17
y = -3(-3) + 17
y = 9 + 17
y = 26
This means it has only one solution and the solution is (-3,26)
=D
METROOOBOOOMINONTHETRACK
I need help solving this please
Trigonometry

Answers
Answer:
11. x = 32.6°
12. x = 27.0
Step-by-step explanation:
Question 11
\(\sin(\theta)=\dfrac{\textsf{opposite side}}{\textsf{hypotenuse}}\)
Given:
\(\theta\) = xside opposite angle = 7hypotenuse = 13\(\implies \sin(x)=\dfrac{7}{13}\)
\(\implies x=\sin^{-1}\left(\dfrac{7}{13}\right)\)
\(\implies x=32.6\textdegree \textsf{ (nearest tenth)}\)
Question 12
\(\sin(\theta)=\dfrac{\textsf{opposite side}}{\textsf{hypotenuse}}\)
Given:
\(\theta\) = 64°side opposite the angle = xhypotenuse = 30\(\implies \sin(64\textdegree)=\dfrac{x}{30}\)
\(\implies x=30\sin(64\textdegree)\)
\(\implies x=27.0\textsf{ (nearest tenth)}\)
Draw the line of reflection that reflects △ABC onto triangle Δ A'B'C'

Answers
The line for the graph x=1 is the line of reflection that reflects triangle ABC onto triangle A'B'C'.
You have to find the middle points between each pair of identical points and then join them.

The solution is, x = 1 will be the line of reflection.
What is reflection?In mathematics, a reflection (also spelled reflexion) is a mapping from a Euclidean space to itself that is an isometry with a hyper plane as a set of fixed.
here, we have,
from the given information , we get,
Coordinates of the vertex A → (-4, -6)
Coordinates of the vertex A' → (6, 6)
Since, y-coordinates are same opposite in notation,
Therefore, by the rule of reflection, line of reflection will be a line parallel to y-axis.
And points A and A' will be equidistant from the line of reflection.
Midpoint between A and A' = (x1+x2/2) , (y1+y2/2)
= (-4+6 / 2 , -6+6 /2)
= (1, 0)
Therefore, x = 1 will be the line of reflection.
To learn more on reflection click:
brainly.com/question/15487308
#SPJ2