Indicate the method you would use to prove the two triangles congruent if new method applies, enter none. SSS, ASA, AAS, SAS, none.

Answers
The two triangles are congruent based on the ASA Congruence Postulate.
What is the ASA Congruence Postulate?The ASA Congruence Postulate states that if two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the two triangles are congruent.
The image shown above shows two triangles that has three pairs of congruent triangles and a pair of corresponding congruent sides.
Therefore, both triangles are congruent by the ASA Congruence Postulate.
Learn more about the ASA on:
https://brainly.com/question/2398724
#SPJ1
Related Questions
6x - 7 if x=8
Answers
.41
.68
.61
.40
Answers
Answer:
I think it's the 3rd one 61 hope this helps
6*8 -7 = 41
Ans :41
X^2-24+6=0
Розв’язати квадратне рівняння

Answers
Answer:
X=√18
Step-by-step explanation:
X^2-18=0
X^2=18
X=√18
Can anyone help me with this please? Thanks again.
In a picture, a man measures 2.3 cm. His actual height is 1.78 m. He is standing beside a flagpole that measures 7.6 cm in the picture. What is the actual height of the flagpole, to the nearest tenth of a meter?
Answers
Answer:
5.88 meters
Step-by-step explanation:
This is a problem of scale factor which uses the concept of ratio.
scale factor is the ratio of length of actual figure to length of its model.
Example: if an architect is drawing design for a building
if height of building is 100 meter but he is drawing this on paper of 1 meter then scale factor will 100/ 1= 100: 1.
It means that for every 100 meter of length of building, it can be represented by 1 meter of its model.
Thus if a building has length 200 meter then its model will be of 200/100 = 2 meter length.
______________________________________
We will solve the given problem based on use of this concept.
Height of man = 1.78 meter
since in picture unit of measure is in cm, lets convert 1.78 meter to centimetre.
1 meter = 100 cm
1.78 meter = 100* 1.78 cm = 178 cm
height of man in picture = 2.3 cm
Scale factor = actual Height of man/Height of man in picture
= 178/2.3 = 77391
_________________________________________
ratio of actual height of flagpole / height of flagpole = actual Height of man/Height of man in picture
Substituting the value given in problem we have
actual height of flagpole/7.6 = 178/2.3
=>actual height of flagpole = (178/2.3)* 7.6 = 588.172 cm.
Thus height of pole is 588.172 cm.
In meter, height of pole is 588.172*100 cm
height of pole is 5.88 meters
Write an equation in slope-intercept form for the line that passes through (8,1) and (4,3)
.
y=−2x+5
y=−1/2x+5
y=1/2x+5
y=−1/2x+1/5
Answers
Find slope
Then solve for B using either given point
Slope = m= (y2-y1)/(x2-x1)
Slope intercept form is y= mx+b
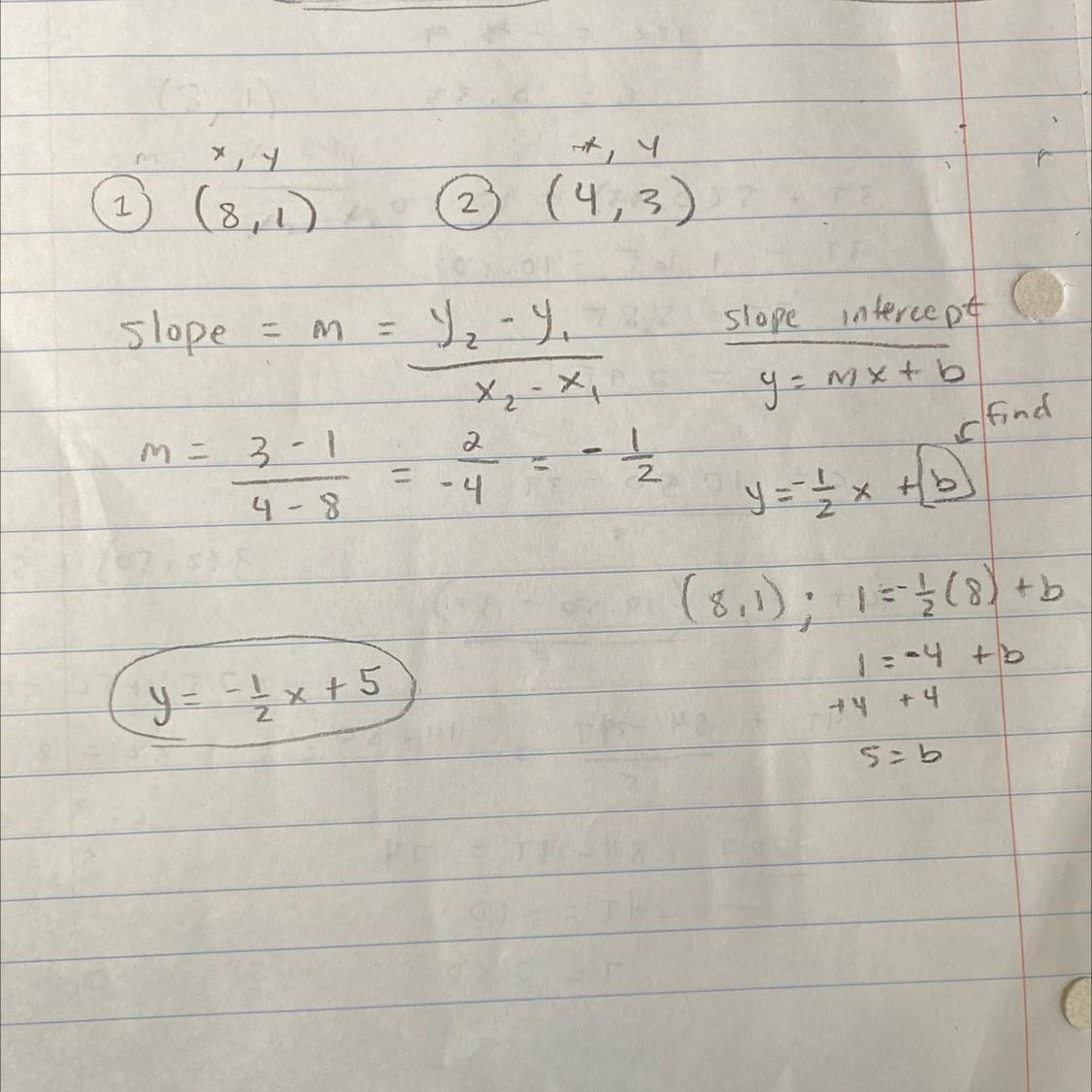
how do I know what is the segment of a triangle?
Answers
The segment of a triangle is the median of the triangle. This is the line that join a vertex of the triangle to the opposite side of the triangle.

Here is the probability model for the political affiliation of a randomly chosen adult in the United States: Political affiliationRepublican Independent Democrat Other Probability 026 0.39 0.33 This probability model is a) finite b) equally likely c) continuous
Answers
The answer is finite.
This is because the probability model lists the probabilities for four distinct and mutually exclusive outcomes (Republican, Independent, Democrat, and Other) and the sum of these probabilities equals 1.
Therefore, the probability model is a finite model, as opposed to a continuous model which deals with probabilities over an infinite range of outcomes.
Learn more about probability: https://brainly.com/question/11234923
#SPJ11
find the mean of the integers
5,-7,12,-10,15
Answers
68/125 Write a fraction as an equivalent fraction with a power of 10 in the denominator.Then write the fraction as a decimal
Answers
Answer:
\(\huge\boxed{\dfrac{68}{125}=0.544}\)
Step-by-step explanation:
\(\dfrac{68}{125}=\dfrac{68\cdot8}{125\cdot8}=\dfrac{544}{1,000}=0.544\)
Which statements are true regarding quadrilateral ABCD? Check all that apply. ABCD has congruent diagonals. ABCD is a rhombus. ABCD is not a rectangle. ABCD is not a parallelogram. ABCD has four congruent angles
Answers
Answer:
ABCD has congruent diagonals.
ABCD is a rhombus.
ABCD has four congruent angles
Step-by-step explanation:
The following statements would be considered true
1. The quadrilateral ABCD could have the congruent diagonals as the diagonals are perpendicular
2. ABCD would be treated as the rhombus as it is a regular quadrilateral
3. ANd, It Have the four congruent angles that means the four angles be 90 degrees
The other statements would be false.

Answer:
A,B,E
Step-by-step explanation:
Edge 2021
Let f be a function of two variables that has continuous partial derivatives and consider the points
A(8, 9),
B(10, 9),
C(8, 10),
and
D(11, 13).
The directional derivative of f at A in the direction of the vector AB is 9 and the directional derivative at A in the direction of
AC is 2. Find the directional derivative of f at A in the direction of the vector AD.
(Round your answer to two decimal places.)
Answers
Answer:
The directional derivative of f at A in the direction of \(\vec{u}\) AD is 7.
Step-by-step explanation:
Step 1:
Directional of a function f in direction of the unit vector \(\vec{u}=(a,b)\) is denoted by \(D\vec{u}f(x,y)\),
\(D\vec{u}f(x,y)=f_{x}\left ( x ,y\right ).a+f_{y}(x,y).b\).
Now the given points are
\(A(8,9),B(10,9),C(8,10) and D(11,13)\),
Step 2:
The vectors are given as
AB = (10-8, 9-9),the direction is
\(\vec{u}_{AB} = \frac{AB}{\left \| AB \right \|}=(1,0)\)
AC=(8-8,10-9), the direction is
\(\vec{u}_{AC} = \frac{AC}{\left \| AC \right \|}=(0,1)\)
AC=(11-8,13-9), the direction is
\(\vec{u}_{AD} = \frac{AD}{\left \| AD \right \|}=\left (\frac{3}{5},\frac{4}{5} \right )\)
Step 3:
The given directional derivative of f at A \(\vec{u}_{AB}\) is 9,
\(D\vec{u}_{AB}f=f_{x} \cdot 1 + f_{y}\cdot 0\\f_{x} =9\)
The given directional derivative of f at A \(\vec{u}_{AC}\) is 2,
\(D\vec{u}_{AB}f=f_{x} \cdot 0 + f_{y}\cdot 1\\f_{y} =2\)
The given directional derivative of f at A \(\vec{u}_{AD}\) is
\(D\vec{u}_{AD}f=f_{x} \cdot \frac{3}{5} + f_{y}\cdot \frac{4}{5}\)
\(D\vec{u}_{AD}f=9 \cdot \frac{3}{5} + 2\cdot \frac{4}{5}\)
\(D\vec{u}_{AD}f= \frac{27+8}{5} =7\)
The directional derivative of f at A in the direction of \(\vec{u}_{AD}\) is 7.
Make f the subject of the formula below

Answers
If we make f the subject of the formula, then f = (3 + 4d)/(3 + d)
We are given a formula in which d = 3(1 - f)/(f - 4). We have to make f the subject of the formula. To make a variable the subject of the formula, we isolate it to the left-hand side of the equation with no other variable written along with it.
So, in this question, we will isolate f on the left-hand side of the equation and we will make f the subject of the formula. We are given that
d = \(\frac{3(1-f)}{f - 4}\)
When we cross-multiply this equation, we get
d(f -4) = 3(1 -f)
fd - 4d = 3 - 3f
Combine all the terms having variable f to the left-hand side.
fd + 3f = 3 + 4d
f( d + 3) = 3 + 4d
f = \(\frac{(3 + 4d) }{(3 + d)}\)
Therefore, by making f the subject of the formula, we get
f = (3 + 4d)/(3 + d)
To learn more about the subject of the formula;
https://brainly.com/question/29401399
#SPJ1
Supposed the total sales for Calculus Department Store was 20 000 00.00 Pesos. What wasa the amount of sales in the clothing Department?
others: 6%
supermarket: 40%
furniture: 12%
Applicances: 14%
clothing: 28%
Answers
Answer:
Step-by-step explanation:
To find the amount of sales in the clothing department, we need to calculate 28% of the total sales.
Total sales: 20,000,000.00 Pesos
Amount of sales in the clothing department:
Sales = 28% of total sales
Sales = 28/100 * 20,000,000.00
Sales = 0.28 * 20,000,000.00
Sales = 5,600,000.00 Pesos
Therefore, the amount of sales in the clothing department is 5,600,000.00 Pesos.
How much would Haiti’s balance be from account two over 3.4 years round to two decimal place

Answers
Solution:
Given:
Account 2 details:
Assume a year is 365 days;
\(\begin{gathered} P=\text{ \$}8100 \\ t=3.4years \\ r=5.1\text{ \%}=\frac{5.1}{100}=0.051 \\ n=365days \end{gathered}\)Using the compound interest formula to get the amount;
\(A=P(1+\frac{r}{n})^{nt}\)Hence, substituting the values;
\(\begin{gathered} A=8100(1+\frac{0.051}{365})^{365\times3.4} \\ A=8100(1+\frac{0.051}{365})^{1241} \\ A=9633.55 \end{gathered}\)Therefore, the balance in account 2 will be $9633.55
given are five observations collected in a regression study on two variables. xi 2 6 9 13 20 yi 7 18 9 26 23 which of the following scatter diagrams accurately represents the data?
Answers
the regression equation:
y = 0.9x+ 7.5
given that:
Xi: 2; 6; 9; 13; 20
Yi: 7; 18; 9; 26; 23
from the given data we have:
∑x = 2+6+9+13+20 = 50
∑y = 7+18+9+26+23 = 83
Also, we need to calculate:
∑XY = 2 × 7+ 6 × 18+ 9× 9+ 13 × 26+ 20×23 = 1001
∑\(x^{2}\) = \(2^{2}\) + \(6^{2}\)+\(9^{2}\) + \(13^{2}\)+ \(20^{2}\) = 690
∑\(y^{2}\)= \(7^{2}\)+ \(18^{2}\) + \(9^{2}\) + \(26^{2}\) +\(23^{2}\) = 1659
the slope b is calculated:
b = ∑XY - ∑x × ∑y/n ÷ ∑ - (∑x)^2 /n
now we need to substitute the above values in the equation:
b = 1001 - 50×83 /5 ÷ 690 - (50)^2/5
b= 0.9
the y-intercept (a) is :
a = y - bx
where
y = ∑y/n = 83/5 = 16.6
x = ∑x/n = 50/5 = 10
now substitute these values
a = 16.5 - 0.9 × 10
a = 7.5
the regression equation:
y = bx + a
now ,
y = 0.9x+ 7.5
To learn more about regression equation:
brainly.com/question/14180189
#SPJ4
Which equation represents a line which is parallel to the line 7y-4x=-141. y= 7/4x+22. y = 4/7x-13. y = -7/4x+64. y = -4/7x-3
Answers
The general equation of a line is y = mx+b, m being the slope and b the intercept on the y-axis.
We are given the line 7y-4x=-14, let's organize the equation like the general form:
\(\begin{gathered} 7y-4x=-14 \\ 7y=4x-14 \\ y=\frac{4}{7}x-2 \end{gathered}\)In order to be parallel to your line, a line has to have the same slope as your line. So the slope has to be 4/7.
Thus any line parallel to the line y=4/7x-2 has an equation of the form y=4/7x+b, where b is any number.
By looking at the answer options, we can select the second option y= 4/7x-1
Which of the following possibilities will form a triangle?
Side = 14 cm, side 6 cm,side = 9 cm
Side 13 cm, side 5 cm, side 8 cm
side = 14 cm, side = 7 cm, side = 6 cm
Side = 13 cm, side = 6 cm, side = 6 cm
please help me
Answers
Using the sum of the sides of the triangle, it is found that the possibility that will form a triangle is:
Side = 14 cm, side 6 cm,side = 9 cm
What is the condition of the sum of the sides of the triangle?In a triangle, the sum of the lengths of the two smaller sides has to be greater than the length of the greater side.
In this problem:
Possibility 1 forms a triangle, as 6 + 9 > 15.Possibility 2 does not form triangle, as 5 + 8 = 13.Possibility 3 does not form triangle, as 7 + 6 < 14.Possibility 4 does not form triangle, as 6 + 6 < 13.Hence the correct option is:
Side = 14 cm, side 6 cm,side = 9 cm
To learn more about the sum of the sides of the triangle, you can take a look at https://brainly.com/question/25401493
Find the volume of the rectangular prism.

Answers
Answer: .75 or 3/4
Step-by-step explanation:
Answer:30/40
Step-by-step explanation:
to answer this question, we need to calculate 5/8x3/5x2
5/8 x 3/5 is just both top and bottom of each multiplied, 5 x 3 which is 15 and 8 x 5 which is 40, so 15/40 x 2/1 = 30/40
also try figure it out on your own.
Estimate $10.01 + $7.07 using front-end estimation.
Answers
Answer:
17
Step-by-step explanation:
You would make the 10.01 a 10 and the 7.07 a 7.
If a2 = i, where i is the identity matrix, which matrix correctly represents matrix a?
Answers
\(A=\left[\begin{array}{ccc}3&-2\\4&-3\end{array}\right]\)
We can find the A as shown below:
Given A^2=I
We know that A^2=A×A
And \(I=\left[\begin{array}{ccc}1&0\\0&1\end{array}\right]\)
So, \(A^2=\left[\begin{array}{ccc}1&0\\0&1\end{array}\right]\)
Let \(A=\left[\begin{array}{ccc}3&-2\\4&-3\end{array}\right]\)
\(A^2=\left[\begin{array}{ccc}3&-2\\4&-3\end{array}\right] \left[\begin{array}{ccc}3&-2\\4&-3\end{array}\right]\)
\(A^2=\left[\begin{array}{ccc}9-8&-6+6\\12-12&-8+9\end{array}\right]\)
\(A^2=\left[\begin{array}{ccc}1&0\\0&1\end{array}\right]\)
Hence, \(A=\left[\begin{array}{ccc}3&-2\\4&-3\end{array}\right]\)
Hence, option C is correct
Learn more about matrix here:
https://brainly.com/question/94574
#SPJ1
Disclaimer: Given question is incomplete. Complete question is attached.

The bottom of a ladder is 1.5 m from the base of a vertical wall. The gradient
of the ladder is 3. How far up does the top of the ladder touch the wall?
Answers
Let p(x) = 7x + 5 and r(x) = x - 1. Find and evaluate (r x p) (5)
Answers
Answer: 39
Step-by-step explanation:
Given
P(x)=7x+5
r(x)=x-1
r(p(x))=7x+5-1=7x+4
so, r(p(5))
\(\Rightarrow r(p(5))=7\times 5+4=35+4=39\)
Find the distance between the two points in simplest radical form.
(-5,6) and (-3,-1)
Answers
Answer:
√53
Step-by-step explanation:
Formula
d = sqrt( (x2 - x1)^2 + (y2 - y1)^2 )
Givens
x1 = -5
x2 = -3
y1 = 6
y2 = - 1
Solution
d = sqrt( ( -3 - -5)^2 + (-1 - 6)^2 )
d = sqrt( ( -3 + 5)^2 + (-7)^2 )
d = sqrt( 2^2 + 49)
d = sqrt(4 + 49)
d = sqrt(53)
The length of the parallel sides of a trapezoid are 15 m and 25 m. If the perpendicular distance between the parallel sides is 10 m, what is the area of the trapezoid?
Answers
Answer:
Area of trapezoid = 200 m²
Step-by-step explanation:
Parallel side1 a= 15m
Parallel side2 b= 25m
Perpendicular distance h = 10 m
We need to find area of the trapezoid.
The formula used to find area of the trapezoid is: \(Area \ of \ trapezoid=\frac{a+b}{2}h\)
Putting values and finding area of the trapezoid:
\(Area \ of \ trapezoid=\frac{a+b}{2}h\\Area \ of \ trapezoid=\frac{15+25}{2}\times 10\\Area \ of \ trapezoid=40\times5\\Area \ of \ trapezoid=200 \ m^2\)
So, area of trapezoid = 200 m²
The product of a number and 2 is 1. Find eight times the number.
Answers
Answer:
I would think that it would be 8
Step-by-step explanation:
1-2= (-1)= -1+2=1
I think it's 8. 8 times the number of 1 is well...8.
Step-by-step explanation:
x = the number
x * 2 = 1
soooo x = 1/2
then 8 * 1/2 = 4
identify a characteristic of change managers that an organization should consider when employing people.
Change managers are nonconformists who take risks.
Having a large number of conformist is effective for an organization.
Change managers are usually regarded as peacemakers who follow rules.
Having a large number of radical innovators is effective for an organization.
Answers
While hiring change managers, businesses should take into account their nonconformist, risk-taking nature.
To successfully implement organizational change efforts, change managers must question the status quo, take measured risks, and foster creativity. Organizational stability and routine tasks may be maintained more successfully with a large number of conformists, but change managers need a distinct skill set. They must be able to think creatively, try out novel concepts, and deal with ambiguity and uncertainty.
Option 3: Being seen as a rule-following peacemaker may be an asset in some situations, but it is not always necessary for a change manager. Similarly, having a lot of radical innovators (option 4) could backfire if there isn't a balance with other qualities and abilities crucial for effective change management.
Learn more about radical innovation :
https://brainly.com/question/14298323?
#SPJ4
The complete question is:
identify a characteristic of change managers that an organization should consider when employing people.
→ Change managers are nonconformists who take risks.
→ Having a large number of conformist is effective for an organization.
→ Change managers are usually regarded as peacemakers who follow rules.
→ Having a large number of radical innovators is effective for an organization.
While hiring change managers, businesses should take into account their nonconformist, risk-taking nature.
To successfully implement organizational change efforts, change managers must question the status quo, take measured risks, and foster creativity. Organizational stability and routine tasks may be maintained more successfully with a large number of conformists, but change managers need a distinct skill set. They must be able to think creatively, try out novel concepts, and deal with ambiguity and uncertainty.
Option 3: Being seen as a rule-following peacemaker may be an asset in some situations, but it is not always necessary for a change manager. Similarly, having a lot of radical innovators (option 4) could backfire if there isn't a balance with other qualities and abilities crucial for effective change management.
Learn more about radical innovation here:
brainly.com/question/14298323?
#SPJ11
Joseph is signing up for a gym membership with a one-time fee to join and then a monthly fee to remain a member. Let CC represent the total cost of the gym membership over t months. A graph of CC is shown below. Write an equation for CC then state the slope of the graph and determine its interpretation in the context of the problem.
Answers
Answer:
The equation for the total cost of the gym membership over t months is CC = Jo + M * t, where Jo represents the one-time fee to join, M represents the monthly fee to remain a member, and t represents the number of months for which the membership is valid.
The slope of the graph is M, the monthly fee to remain a member. The interpretation of the slope in the context of the problem is that it represents the cost per month of remaining a member of the gym.
Robert is told the size of angle BAC in degrees and he is then asked to calculate
the length of the line BC. He uses his calculator but forgets that his calculator
is in radian mode. Luckily he still manages to obtain the correct answer. Given
that angle BAC is between 10° and 15°, use graphing software to help you find
the size of angle BAC, correct to 2 decimal places.

Answers
The measure of angle BAC is of 14.48º, considering the relations in a right triangle.
What are the relations in a right triangle?There are three relations in a right triangle, presented as follows:
The sine of an angle of the triangle is represented by the length of the opposite side to the angle divided by the length of the hypotenuse.The cosine of an angle of the triangle is represented by the length of the adjacent side to the angle divided by the length of the hypotenuse.The tangent of an angle of the triangle is represented by the length of the opposite side to the angle divided by the length of the adjacent side to the angle.Using a ruler, it is found that the length of the opposite side to angle BAC, of CB, is of 1.5 cm, hence the following relation is established, considering the hypotenuse of 6 cm.
sin(x) = 1.5/6
In which x is the measure of angle BAC.
x can be isolated applying the arc sine function, which is the inverse of the sine, hence:
x = arcsin(1.5/6)
x = 14.48º.
More can be learned about the relations in a right triangle at https://brainly.com/question/26396675
#SPJ1
Consider the following data for a dependent variable y and two independent variables, ₁ and 2. x1 22 30 12 45 11 25 18 50 17 41 6 50 19 75 36 12 59 13 76 17 The estimated regression equation for thi
Answers
69.56 + 0.32x₁ - 0.18x₂ is the equation that fits the given data for the dependent variable y and the two independent variables x₁ and x₂.
The given data for a dependent variable y and two independent variables, x₁ and x₂, are as follows:
x₁: 22, 30, 12, 45, 11, 25, 18, 50, 17, 41, 6, 50, 19, 75, 36, 12, 59, 13, 76, 17
y: 50, 90, 50, 80, 60, 80, 50, 70, 60, 70, 50, 70, 90, 80, 70, 60, 80, 50, 70, 60
The estimated regression equation for the given data is given by:
y = 69.56 + 0.32x₁ - 0.18x₂
Here:
y represents the dependent variable.
x₁ and x₂ are the two independent variables.
Therefore, the equation that fits the given data for the dependent variable y and the two independent variables x₁ and x₂ is y = 69.56 + 0.32x₁ - 0.18x₂.
To learn more about variables, refer below:
https://brainly.com/question/15078630
#SPJ11
A boat can go 756 miles on 63 gallons of gas. How far can it go on 53 gallons?
Answers
Answer: 636
Step-by-step explanation:
First, we need to find out how many miles per gallon (mpg) the boat gets
So we need to divide 756 by 63
756/63=12
Now we know the boat gets 12mpg
Now let's multiply 12 by 53
12x53
636 miles
Please help me find the missing length

Answers
Answer:
The tower is 48 ft tall.
Step-by-step explanation:
Refer to the figure attached.
Triangle ACD is similar to triangle BCE.
This means the proportion to some sides is the same, for example:
\(\displaystyle \frac{CE}{CD}=\frac{BE}{H}\)
Substituting the values:
\(\displaystyle \frac{8}{64}=\frac{6}{H}\)
Multiplying by 64H:
\(8H=64*6\)
Dividing by 8:
\(H=64*6/8=48\)
The tower is 48 ft tall.
