let me know if the question is incomplete! ill add it in the comments just in case.
question: if 0
Answers
Related Questions
find an equation of the set of all points equidistant from the points a(−2, 4, 4) and b(5, 2, −3). describe the set.
Answers
The set of all points equidistant from the points A(-2, 4, 4) and B(5, 2, -3) forms a plane. This plane can be described by an equation that represents the locus of points equidistant from A and B.
To find the equation of the plane, we can first calculate the midpoint M between points A and B, which is given by the coordinates (x₀, y₀, z₀) of M, where x₀ = (x₁ + x₂)/2, y₀ = (y₁ + y₂)/2, and z₀ = (z₁ + z₂)/2.
Midpoint M:
x₀ = (-2 + 5)/2 = 3/2
y₀ = (4 + 2)/2 = 3
z₀ = (4 - 3)/2 = 1/2
Next, we calculate the direction vector D from A to B, which is obtained by subtracting the coordinates of A from those of B.
Direction vector D:
dx = 5 - (-2) = 7
dy = 2 - 4 = -2
dz = -3 - 4 = -7
Using the midpoint M and the direction vector D, we can write the equation of the plane as follows:
(x - x₀)/dx = (y - y₀)/dy = (z - z₀)dz
Substituting the values we calculated earlier, the equation becomes:
(x - 3/2)/7 = (y - 3)/(-2) = (z - 1/2)/(-7)
This equation represents the set of all points equidistant from points A(-2, 4, 4) and B(5, 2, -3), and it describes a plane in three-dimensional space.
Learn more about equidistant here
https://brainly.com/question/29886221
#SPJ11
12x-3x+4=5x-16 Find x
Answers
Answer:
x = -5
Step-by-step explanation:
12x - 3x + 4 = 5x - 16
9x + 4 = 5x - 16
9x - 5x = -4 - 16
4x = -20
x = -5
Answer:
\(x=-5\)
Find the area under the standard normal curve to the left of z=2.06. round your answer to four decimal places.
Answers
The area under the standard normal curve to the left of z = 2.06 is approximately 0.9803.
The normal distribution function, also known as the Gaussian distribution or bell curve, is a probability distribution that is symmetric, bell-shaped, and continuous. It is defined by two parameters: the mean (μ) and the standard deviation (σ).
The normal distribution is widely used in statistics and probability theory due to its many desirable properties and its applicability to various natural phenomena. It serves as a fundamental distribution for many statistical methods, hypothesis testing, confidence intervals, and modeling real-world phenomena.
To find the area under the standard normal curve to the left of z = 2.06, you can use a standard normal distribution table or a calculator with a normal distribution function. The standard normal distribution is a normal distribution with a mean of 0 and a standard deviation of 1.
Using a standard normal distribution table, the area to the left of z = 2.06 can be found by looking up the corresponding value in the table. However, since the standard normal distribution table typically provides values for z-scores up to 3.49, we can approximate the area using the available values.
The closest value in the standard normal distribution table to 2.06 is 2.05. The corresponding area to the left of z = 2.05 is 0.9798. This means that approximately 97.98% of the area under the standard normal curve lies to the left of z = 2.05.
Since z = 2.06 is slightly larger than 2.05, the area to the left of z = 2.06 will be slightly larger than 0.9798.
Therefore, rounding the answer to four decimal places, the area under the standard normal curve to the left of z = 2.06 is approximately 0.9803.
To know more about function visit:
https://brainly.com/question/31062578
#SPJ11
PLEASE answer THIS QUESTION CORRECTLY AND ILL MARK YOU AS THE BRAINLIEST

Answers
Answer:
137
Step-by-step explanation:
I hope this helps
Please help!!
a =
4
6
9

Answers
Answer:
a=
Step-by-step explanation:
: Prove that a) X'Y' + X'Y +XY = X' +Y b) A'BC' + ABC' + BC'D = BC' Find the complement of the following function a) WX(Y'Z+YZ') + W'X'(Y' +Z)(Y+Z') b) (A+B'+C') (A'B' +C)(A + B'C') Find Dual of question 2 (a, b),
Answers
a) X'Y' + X'Y + XY simplifies to X' + Y.
b) A'BC' + ABC' + BC'D simplifies to BC'.
Complement of the functions:
a) Complement is W' + X' + YZ.
b) Complement is (A' + B + C)(A'B' + C' + A'B).
a) To prove X'Y' + X'Y + XY = X' + Y, we can use Boolean algebra identities:
X'Y' + X'Y + XY
= Y'(X' + X) + XY(Distributive Law)
= Y' + XY(X + X' = 1)
= X' + Y(Commutative Law)
Therefore, X'Y' + X'Y + XY simplifies to X' + Y.
b) To prove A'BC' + ABC' + BC'D = BC', we can simplify the expression using Boolean algebra:
A'BC' + ABC' + BC'D
= BC'(A' + A) + BC'D (Distributive Law)
= BC' + BC'D(A + A' = 1)
= BC'(BC' + BC'D = BC' + BC'(1) = BC')
Hence, A'BC' + ABC' + BC'D simplifies to BC'.
Complement of the given functions:
a) The complement of WX(Y'Z + YZ') + W'X'(Y' + Z)(Y + Z') is W' + X' + YZ.
b) The complement of (A + B' + C')(A'B' + C)(A + B'C') is (A' + B + C)(A'B' + C' + A'B).
Learn more About Distributive Law from the given link
https://brainly.com/question/25224410
#SPJ11
6. An airplane is headed north with a constant velocity of 430 km/h. the plane encounters a west wind blowing at 100 km/h. a) How far will the plane travel in 2 h? b) What is the direction of the plan
Answers
The direction of the plane is still north, because the plane is moving forward at a greater speed than the wind is pushing it back.
a) The plane will travel 760 km in 2 hours. To solve this, we need to first calculate the resultant velocity of the plane.
The resultant velocity is 430 km/h in the northwards direction plus the wind velocity of 100 km/h in the westwards direction.
This results in a velocity vector of $(430)² + (100)² = 468.3$ km/h in the northwest direction.
As the plane has a velocity of 468.3 km/h in this direction, it will travel $(468.3)(2)$ = 936.6 km in 2 hours.
b) The direction of the plane is northwest.
Therefore, the direction of the plane is still north, because the plane is moving forward at a greater speed than the wind is pushing it back.
Learn more about the velocity here:
https://brainly.com/question/19979064.
#SPJ1
/\(\frac{x-9}{15} =\frac{2x-9}{10\\}\)
Answers
Step-by-step explanation:
\( \frac{x - 9}{15} = \frac{2x - 9}{10} \\ \)
\( \frac{x - 9}{3} = \frac{2x - 9}{2} \\ \)
\(2( x - 9) = 3(2x - 9) \\ \)
\(2x - 18 = 6x - 27\)
\(27 - 18 = 6x - 2x\)
\(9 = 4x\)
\(x = \frac{9}{4} \\ \)
how many time 2/3 can go into 16
Explanation pls!!
Answers
Answer:
24 times
Step-by-step explanation:
16 divided by 2/3 is 24
hope this helped!
The equation below describes a proportional relationship between x and y. What is the constant of proportionality?
y=2/9x
Answers
Answer:
2/9 is it
Step-by-step explanation:
pls help ty ty i really dont cant finish my geometry hw thanks

Answers
Answer:
m<DEB=113°
Step-by-step explanation:
Hokay, so-
given m<ABH=67°, you know that
m<CBF=67° | verticle angles
and you know that:
m<ABF=m<CBH | verticle angles
--> 67°+67°+m<ABF+m<CBH=360°
134°+m<ABF+m<CBH=360°
m<ABF+m<CBH=226°
x+x=226°
2x=226°
x=113°
x=m<ABF=m<CBH=113°
m<BFE=m<CBF=67° | alt. interior angles
Since you are also given BE=BF, you know that BEF is an isos. triangle, meaning:
--> m<BEF=m<BFE=67°
now that you know what m<BEF is,
180°-m<BEF=m<DEB
180°-67°=m<DEB
m<DEB=113°
orrrrr
you could have skipped all that and just figured it out in the first half when you found x=113°, and see that
m<ABF=m<BFG | alt. int. angles
to realize that m<DEB=113° but I'm typing this in the middle of my geo RSM class so my brains pretty much shut off now qwq
find the margin of error for the given values of c, σ, and n. c = 0.98, σ = 0.78, n = 150
Answers
The margin of error is 2.326 for the supplied values of c, σ, and n, which are 0.98, 0.78, and 150 respectively.
what is margin ?Margin is the term used to describe the equity that a trader has in their account. Using funds borrowed from a broker to buy stocks is referred to as "marging" or "buying on margin." Instead of a typical brokerage account, you must have a margin account to execute this. Beginning with your gross profit, which is the distinction between revenue and COGS, you may compute profit margin. Find the percentage of revenue that represents gross profit next. Calculate it by dividing your gross profit by your revenue. You can calculate your margin % by multiplying the sum by 100.
Given that,
Population standard deviation =
= 0.78
Sample size = n =150
α = 1 - 98% = 1 - 0.98 = 0.02
α= 2 = 0.02/ 2 = 0.01
Z*α = 2 = 0.01 = 2.326 ( Using z table )
Margin of error = E = Z
The margin of error is 2.326 for the supplied values of c, σ, and n, which are 0.98, 0.78, and 150 respectively.
To know more about margin visit :-
https://brainly.com/question/28856941
#SPJ4
What is the value of 3x- (y / 2+ 5) when x=3.5 and y= 4?
Answers
Answer:
3.5
Step-by-step explanation:
3x -(y / 2+ 5) x = 3.5 and y = 4
= 3(3.5) -(4/2 + 5)
= 3(3.5) -(2 + 5)
= 10.5 -(2 + 5)
= 10.5 -(7)
= 10.5 - 7
= 3.5
Find the value of x in 3x + 4y = 12 and 9x - 4y = 24.
A.-3
B.3
C.0.75
D.-0.75
Answers
Answer:
B. x=3
Step-by-step explanation:
3x+4y=12
9x-4y=24
Add 9x and 3x
Subtract -4y from 4y which will cancel out
Add 12 and 24
12x=36
divide both sides by 12
x=3
Please help me out with this algebra2

Answers
Answer:
Step-by-step explanation:
a.) S(t)=9t-4
S(4)= 9(4)-4
= 36-4
S(4)=32
b.) S(4) means the number of people who got the flu in 4 days.
c.) S(t)=23 t=23/s
d.) I'm not sure on this one. S(t)=23 means 23 people got the flu in t days
e.) Choose values as inputs- these will be your x values, your putput will be the y.
I think I did this right, Hope this helps :)
Winter 2023 (online ) operties of Exponents Simplify. Write the answer using positive exponents only. (2x^(6)y^(4))^(4)
Answers
The answer using positive exponents only is 16x^(24)y^(16).
To simplify the expression (2x^(6)y^(4))^(4), we need to use the properties of exponents. Specifically, we need to use the property that states (a^(m))^n = a^(m*n). This means that when we raise a power to another power, we multiply the exponents.
Using this property, we can simplify the expression as follows:
(2x^(6)y^(4))^(4) = 2^(4) * x^(6*4) * y^(4*4) = 16 * x^(24) * y^(16)
So, the simplified expression is 16x^(24)y^(16).
Therefore, the answer using positive exponents only is 16x^(24)y^(16).
For more such questions on Properties of exponents.
https://brainly.com/question/1807508#
#SPJ11
Refer to Problems 1-3 to solve Problems 4–6. The first one is done for you. 4. A scale factor between 0 and 1 produces a similar figure that is smaller than the original figure. 5. In Problem 2, YZ = _=4V5, and UV = v=2v5. The ratio of YZ to UV in simplest form is 6. If one polygon can be mapped to another by a series of then the polygons are Original content Copyright © by Houghton Mifflin Harcourt. Additions and changes to the original content are the responsibility 218
Answers
The ratio of YZ to UV is 2:1
1) Considering that the distance between YZ is 4√5 and the distance between points U and V is 2√5 the ratio of YZ to UV can be found through this:
\(\frac{YZ}{UV}=\frac{4\sqrt[]{5}}{2\sqrt[]{5}}\)2) Let's rationalize it by multiplying both numerator and denominator by √5 to simplify removing the radicals on the denominator.
\(\frac{YZ}{UV}=\frac{4\sqrt[]{5}}{2\sqrt[]{5}}\cdot\frac{\sqrt[]{5}}{\sqrt[]{5}}=\frac{4\sqrt[]{5^2}}{2\sqrt[]{5^2}}=\frac{4\cdot5}{2\cdot5}=\frac{2}{1}\)3) So the ratio of YZ to UV is 2:1
can you please help me with Michelson Morley , methods or
procedure ,labeled tables that will allow me to draw the graph ,
also draw the graph for me.
answer all questions correctly step by step
Answers
The Michelson-Morley experiment was conducted in 1887 to detect the existence of the luminiferous ether, which was thought to be the medium through which light traveled.
Here is the procedure for the Michelson-Morley experiment:
1. Set up a light source, a half-silvered mirror, two mirrors, and two detectors in a square configuration.
2. Split the light beam using the half-silvered mirror so that one beam goes to one mirror and the other beam goes to the other mirror.
3. Reflect the beams back to the half-silvered mirror and combine them to produce an interference pattern.
4. Rotate the entire apparatus by 90 degrees and repeat the measurement.
5. Compare the interference patterns from the two orientations.
If there is a luminiferous ether, the speed of light should be faster in the direction of the ether flow and slower in the perpendicular direction. This should produce a difference in the interference patterns.
However, the Michelson-Morley experiment showed that there was no difference in the interference patterns, indicating that the luminiferous ether did not exist.
Learn more about Michelson-Morley experiment: brainly.com/question/2603200
#SPJ4
#1Change from standard form to vertex formy= x²-8x+15
Answers
Therefore, the vector form of the equation y = x² - 8x + 15 is y = (x - 4)² + 14. The vertex of the parabola is at the point (4, 14).
To convert the quadratic equation y = x² - 8x + 15 from standard form to vertex form, we need to complete the square by adding and subtracting a constant term. Here's the step-by-step explanation:
Factor the coefficient of x²: The coefficient of x² is 1, so we don't need to factor it.
Group the x terms: Rewrite the quadratic equation as y = (x² - 8x) + 15.
Complete the square: To complete the square, we need to add and subtract a constant term that will make the expression inside the parentheses a perfect square trinomial. The constant we need to add is half of the coefficient of x, squared: (8/2)² = 16.
y = (x² - 8x + 16 - 16) + 15 // add and subtract 16
y = (x - 4)² - 1 + 15 // factor and simplify
Simplify: Now we can simplify the expression by combining the constants -1 and 15 to get 14.
y = (x - 4)² + 14
To know more about vector,
https://brainly.com/question/30907119
#SPJ11
Melissa has 120 vanilla cake pops to sell. Each vanilla cake pops is covered with one topping. 1/2 of the cake pops are covered with chocolate sprinkles. 1/3 of the cake pops are covered with strawberry sprinkles. * the rest are covered with green sprinkles. How many cake pops are covered with green sprinkles?
Answers
Answer:
The Answer is 20 cake pops are covered with green sprinkles.
Step-by-step explanation:
So if you have 1/2 choclate, 1/3 strawberry, and the rest are green, you first need to convert the Chocolate and the Strawberry into the same fraction. As shown:
Chocolate: 1/2=3/6
Strawberry:1/3=2/6
The rest are Green sprinkles.
So, your equation would be:
Chocolate sprinkles + Strawberry Sprinkles + Green Sprinkles = Total
And their are 5/6 of Chocolate and Strawberry Sprinkles...
That would mean 100 Chocolate and Strawberry Sprinkles!
Because 1/6 of 120 is 20 and multiply that by five and you have 100...
Now that we have that, and we know the rest are green...
we just do 120-100=20
So their you go!
Sorry its long but hope it helps! <3
Which of the following is not the test of congruence AAS SAS SSS SSA?
Answers
Answer:
SAS - SAS should instead be A + SS
Step-by-step explanation:
A server at a restaurant is hoping for a 15% tip from a large party. The
party's bill at the end of the night was $312.00. Write a proportion and
describe how you would solve it to calculate the amount of the tip the
server hopes to receive. Be sure to state your final answer as an amount of
money, rounded to the nearest cent.
*Use the "/" on your keyboard as a fraction bar for ratios when writing the
proportion. For example: I can show that one-half and two-fourths are
proportional by typing "1/2 = 2/4" for the proportion.
Answers
$57 is the amount of the tip the server hopes to receive.
What is Percentage?percentage, a relative value indicating hundredth parts of any quantity.
Given,
A server at a restaurant is hoping for a 15% tip from a large party.
The party's bill at the end of the night was $312.00.
Now we need to find 15% of $312
15% is converted to decimal by dividing with 100
15/100=0.15
Now multiply 0.15 with 380
0.15×380
57
Hence $57 is the amount of the tip the server hopes to receive.
To learn more on Percentage click:
https://brainly.com/question/28269290
#SPJ1
Two out of five students in the ninth grade have braces. If there are 225 students in the
ninth grade, how many have braces?
Answers
Answer:
90
Step-by-step explanation:
when you do 225/5, you find out that the number has been multiplied 45 times, so you should multiply 45 by 2 which is 90
Two airplanes leave an airport at the same time. The first flies 110 km/h in a direction of 280°. The second flies 250 km/h in a direction of 200° After 4hr. how far apart are the planes?
Answers
The distance between the two planes after 4 hours is approximately 150 km.
to find out how far apart the planes are after 4 hours, we can use the concept of vectors.
Let's start by finding the positions of the two planes after 4 hours.
The first plane flies at a speed of 110 km/h in a direction of 280°. To find its position after 4 hours, we can use the formula: distance = speed × time. So, the distance traveled by the first plane is 110 km/h × 4 hours = 440 km.
To determine the position of the first plane, we need to convert the direction (280°) into components. The x-component is given by: cos(280°) × distance = cos(280°) × 440 km. The y-component is given by: sin(280°) × distance = sin(280°) × 440 km.
Similarly, for the second plane, which flies at a speed of 250 km/h in a direction of 200°, the distance traveled after 4 hours is 250 km/h × 4 hours = 1000 km. To determine its position, we need to convert the direction (200°) into components. The x-component is given by: cos(200°) × distance = cos(200°) × 1000 km. The y-component is given by: sin(200°) × distance = sin(200°) × 1000 km.
Now, let's calculate the x and y components for both planes:
For the first plane:
x-component = cos(280°) × 440 km
y-component = sin(280°) × 440 km
For the second plane:
x-component = cos(200°) × 1000 km
y-component = sin(200°) × 1000 km
the distance between the two planes, we can use the distance formula, which is given by: distance = √((x2 - x1)^2 + (y2 - y1)^2), where (x1, y1) and (x2, y2) are the positions of the first and second planes respectively.
Now, substitute the values we calculated into the distance formula:
distance = √((x2 - x1)^2 + (y2 - y1)^2)
distance = √((cos(200°) × 1000 km - cos(280°) × 440 km)^2 + (sin(200°) × 1000 km - sin(280°) × 440 km)^2)
After evaluating the above expression, the distance between the two planes after 4 hours is approximately 150 km.
Learn more about distance with the given link,
https://brainly.com/question/26550516
#SPJ11
96 stickers on 8 pages = _____ stickers per page.
Answers
\( \tt \to \dfrac{96}{8} \)
\( \\ \\ \)
\( \tt \to \: 12 \: stickers\)
Verify:-
12 × 8 = 96
hope it helped u!
Answer:
96/8
I promise you that it os
In a normally distributed sample, 95% of people's heights are between 168 and 184 centimeters. what is the standard deviation of the sample?
A. 2
B. \(2\sqrt{2[
C. 4
D. 8
Answers
Using the Empirical Rule, it is found that the standard deviation of the sample is of:
C. 4
By the Empirical Rule, 95% of the measures are within 2 standard deviations of the mean, that is, between 2 standard deviations below the mean and 2 standard deviations above the mean.
95% of people's heights are between 168 and 184 centimeters, hence, there are 4 standard deviations between 168 and 184 centimeters. Then:
\(4s = 184 - 168\)
\(4s = 16\)
\(s = \frac{16}{4}\)
\(s = 4\)
Hence, option C is correct.
A similar problem is given at https://brainly.com/question/25807482
help me with this question in the picture please :(

Answers
Step-by-step explanation:
possibly A
B. r = C/2π
Explanation:
The problem asks you to solve for r which means you have to get r by itself, or isolate the variable. You would do this by dividing both sides of the equation by 2π. The right side of the equation would cancel out, leaving you with r. The left side of the equation would simply be C/2π because C/2π cannot be simplified.
You could write your answer like this: C/2π = r
Or like this: r = C/2π
Here is my work just in case you're a visual learner:

Figure 2 shows some typical Lorenz curves. They all pass through the points (0,0) and (1, 1) and are concave upward. In the extreme case L(x) = x, society is perfectly egalitarian: the poorest a% of the population receives a % of the total income and so everybody receives the same income. The area between a Lorenz curve y - L(x) and the line y = x measures how much the income distribution differs from absolute equality. The Gini index (sometimes called the Gini coefficient or the coefficient of inequality) is the area between the Lorenz curve and the line y = x(shaded in Figure 3) divided by the area under y = x. (0.8.0.51, 1. (a) Show that the Gini index G is twice the area between the Lorenz curve and the line y = x, that is, 10.4.0.12) G=2 = 2 [[x - L(x)] dx 0 0.2 0.4 0.6 0.8 1 FIGURE 1 Lorenz curve for the US in 2010 (b) What is the value of G for a perfectly egalitarian society (everybody has the same income)? What is the value of G for a perfectly totalitarian society (a single person receives all the income?)
Answers
To summarize, a perfectly egalitarian society has a Gini index of 0, and a perfectly totalitarian society has a Gini index of 1.
The Gini index (G) measures how much the income distribution differs from absolute equality.
It is calculated as the area between a Lorenz curve y - L(x) and the line \(y = x\)divided by the area under \(y = x.\) For a perfectly egalitarian society (where everybody has the same income), the Lorenz curve is a perfect straight line, passing through points (0,0) and (1,1). Since the line y = x is the same as the Lorenz curve in this case, the Gini index (G) will be 0. This means that the income distribution is perfectly equal and that there is no inequality between individuals.On the other hand, a perfectly totalitarian society (where a single person receives all the income) will have a Gini index of 1. This means that there is a huge inequality between individuals, with the single person receiving all of the income.
for such more questions on Lorenz curve
https://brainly.com/question/13595508
#SPJ11
4.53 Referring to Exercise 4.35 on page 127, find the mean and variance of the discrete random variable z = 3X – 2, when X represents the number of errors per 100 lines of code. - 4.35 The random variable X, representing the num- ber of errors per 100 lines of software code, has the following probability distribution: 2 3 4 5 6 0.01 0.25 0.4 0.3 0.04 Using Theorem 4.2 on page 121, find the variance of X. 2
Answers
The variance of z is - 177.1788.
The discrete random variable X representing the number of errors per 100 lines of software code has the following probability distribution. X 2 3 4 5 6 P(X) 0.01 0.25 0.4 0.3 0.04
We can apply Theorem 4.2 to find the variance of X. Theorem 4.2: Let X be a discrete random variable with probability distribution p(x). If the mean of X is μ and the variance of X is σ², then μ = E(X) = ∑x p(x) and σ² = Var(X) = E(X²) - [E(X)]².
Now, we find the mean and variance of the discrete random variable z = 3X – 2.
The mean of z = 3X - 2 is E(z) = E(3X - 2) = 3E(X) - 2.
Hence, the mean is μz = 3(2)(0.01) + 3(3)(0.25) + 3(4)(0.4) + 3(5)(0.3) + 3(6)(0.04) - 2= 14.53.
The variance of z = 3X - 2 is Var(z) = Var(3X) = 9Var(X).
Hence, the variance of X is σz² = 9Var(X) = 9[E(X²) - [E(X)]²] = 9[(2²)(0.01) + (3²)(0.25) + (4²)(0.4) + (5²)(0.3) + (6²)(0.04) - 14.53²] = 34.0021 - 211.1809 = - 177.1788
Therefore, the variance of z is - 177.1788.
Know more about variance here,
https://brainly.com/question/31432390
#SPJ11
Help plzz what's the domain and range
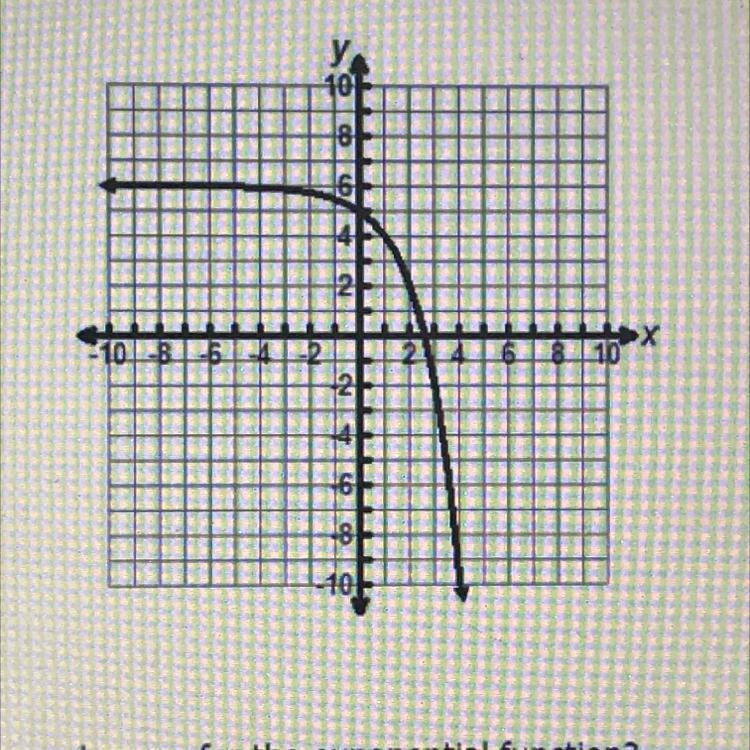
Answers
Answer:
Domain = All real numbers
Range = x < 6
Hope this helps!