Mika has a goal of folding at least 120 paper swans. He can fold 12 paper swans per hour. Which inequaility can Mika use to find h, the number of hours he should fold paper swans to meet or exceed his goal?
Answers
Answer: it would take him 10 hours to make 120 paper
Related Questions
Find the greatest common factor for the terms 6x^5y^8, 8x^3y^9, 12x^2y^4
Answers
Answer:
i dont know
Step-by-step explanation: just for points sorry :(
The height of a helicopter above the ground is given by h = 3.05t3, where h is in meters and t is in seconds. At t = 2.35 s, the helicopter releases a small mailbag. How long after its release does the mailbag reach the ground?
Answers
the height of the mailbag decreases as time increases, and the mailbag reaches the ground at t = 5.33 seconds.
The height of the mailbag after its release is given by the equation h = 3.05t3. At t = 2.35 seconds, the height of the mailbag is h = 3.05 * 2.35 * 2.35 = 39.58 meters. This means that the mailbag is still 39.58 meters above the ground. The equation for the height of the mailbag tells us that the height of the mailbag is decreasing at a rate of 9.15t2 meters per second. This means that the mailbag will take 39.58 / 9.15 = 4.33 seconds to reach the ground.
Therefore, the mailbag will reach the ground after 1 + 4.33 = 5.33 seconds
Here is a table of the height of the mailbag over time:
Time (seconds) | Height (meters)
------- | --------
2.35 | 39.58
2.36 | 35.43
2.37 | 31.28
... | ...
5.33 | 0
As you can see, the height of the mailbag decreases as time increases, and the mailbag reaches the ground at t = 5.33 seconds.
Learn more about decreasing here:
https://brainly.com/question/32610704
#SPJ11
what should be added to {1/-2 - 3/4 of -8/15} so that the sum is the product of -7/50 and 1 1/14 *for grade 7*
Answers
The value that is added on the left-hand side to make the equation equal is -1/100.
What are Mathematical operators?In mathematics, an expression is a group of numbers and operations. The components of a mathematical expression that perform an operation are as follows: multiplication, division, addition, and subtraction.
Given [1/-2 - 3/4 of -8/15],
to add a number so the sum equals the product of -7/50 and 11/14
let the number be x
according to the question,
[1/-2 - 3/4 of -8/15] + x = -7/50*11/14
taking LHS
[1/-2 - 3/4 of -8/15] = -1/2 - (3(-8)/60)
[1/-2 - 3/4 of -8/15] = -1/2 + 24/60
[1/-2 - 3/4 of -8/15] = (-30 + 24)/60
[1/-2 - 3/4 of -8/15] =-6/60 = -1/10
RHS
-7/50*11/14 = -77/700 = -11/100
substitute the values
[1/-2 - 3/4 of -8/15] + x = -7/50*11/14
-1/10 + x = -11/100
x = -11/100 + 1/10
x = (-11 + 10)/100
x = -1/100
Hence -1/100 is added to make the equation equal.
Learn more about Mathematical operators;
https://brainly.com/question/8959976
#SPJ1
Mr. Titus travels from Charlotte to New York City and back 12 times each year. The total distance for each round trip is 623 miles. What is the total number of miles Mr. Titus travels from Charlotte to New York City and back each year? Enter your answer in the box.
Answers
Mr. Titus travels a total of 7476 miles annually between Charlotte, North Carolina, and New York City.
What is an expression?Expression in maths is defined as the relation of numbers variables and functions by using mathematical signs like addition, subtraction, multiplication, and division.
Given that twelve times a year, Mr. Titus makes the trip from Charlotte to New York City and back. Each round trip covers a total distance of 623 miles.
The total distance will be calculated as:-
Distance = 12 x 623
Distance = 7476 miles
Therefore, Mr. Titus' annual mileage between Charlotte, North Carolina, and New York City is 7476 miles.
To know more about an expression follow
https://brainly.com/question/28736515
#SPJ9
How do you convert micrometers to centimeters?
Answers
Divide the number of micrometers by 10,000 to get the equivalent number of centimeters.
To convert micrometers to centimeters, you need to use the conversion factor between the two units. There are 10,000 micrometers in a centimeter.
Here are the steps to convert micrometers to centimeters:
1. Start with the number of micrometers you want to convert.
2. Divide the number of micrometers by 10,000 to get the equivalent number of centimeters.
3. The result is the number of centimeters equivalent to the given number of micrometers.
For example, if you want to convert 50,000 micrometers to centimeters, you would divide 50,000 by 10,000 to get 5 centimeters.
So, the conversion formula is:
centimeters = micrometers ÷ 10,000
To know more about conversion formula click on below link:
https://brainly.com/question/30065592#
#SPJ11
I need help here i dont know how to find it in exponents

Answers
Answer:
s^45/t^81
Step-by-step explanation:
Pedro measured a swimming pool and made a scale drawing. The pool, which is 42 meters long in real life, is 119 centimeters long in the drawing. What scale did Pedro use for the drawing?
Answers
Answer:
The scale that Pedro used for the drawing is: 17:600.
Step-by-step explanation:
A scale of a drawing is expressed as: Drawing length:actual length.
Since you know that the pool is 119 centimeters long in the drawing and 42 meters long in real life, first you have to find the cm in 42 meter taking into account that 1 meter is equal to 100 cm:
1 m → 100 cm
42 m → x
x=(42*100)/1
x=4200 cm
Now, the scale would be:
119:4200
Finally, you need to simplify and you can do it by dividing each number by 7:
17:600
According to this, the answer is that the scale that Pedro used for the drawing is: 17:600.
Samantha often talks on her cell phone while driving. this can be distracting and increases her chance of having an accident. what would your advice be to her?
Answers
Samantha often talks on her cell phone while driving. this can be distracting and increases her chance of having an accident. Don't use the phone at all while driving.
What is rules of driving?
Always move over for pedestrians. Hold your position behind the red-lit school buses. Emergency vehicles with running sirens and flashing lights are approaching. Get rid of any outside influences. Always buckle up when you are driving.I will advise her to refrain from using her phone at all while driving.
Learn more about driving rules
brainly.com/question/10825924
#SPJ4
Please check the attached picture, please answer thoroughly!

Answers
The selection depends on individual needs, preferences, and the intended use of the tiny house.
a) To find the amount of space inside each house, we need to calculate the volume for each design.
House on the left:
Volume = length x width x height = 2.5 m x 18 m x 2.8 m = 126 m³
Triangular house:
Volume of a triangular prism = (base area x height) / 2
Base area = (1/2) x base x height = (1/2) x 4 m x 10 m = 20 m²
Volume = (20 m² x 7 m) / 2 = 70 m³
b) When comparing the environmental impacts of each house, several factors need to be considered:
Positive impacts:
1. Material usage: Tiny houses use fewer materials, reducing resource consumption and waste generation.
2. Energy efficiency: Smaller living spaces require less energy for heating, cooling, and lighting, leading to lower energy consumption.
3. Land utilization: Tiny houses can be built on smaller plots of land, preserving green spaces and reducing urban sprawl.
Negative impacts:
1. Construction materials: Although tiny houses use less material overall, the environmental impact depends on the types of materials used. Sustainable and eco-friendly materials should be prioritized.
2. Water and waste management: Adequate provisions for water supply and waste disposal should be implemented to minimize environmental impacts.
3. Transportation: The transportation of tiny houses to their locations can contribute to carbon emissions if not done efficiently.
c) The choice of design for a tiny house depends on personal preferences and priorities. However, considering the provided information:
The house on the left offers a larger interior space of 126 m³, providing more room for living and storage. It may be suitable for individuals or couples who desire more space and functionality within their tiny house.
The triangular house has a smaller interior volume of 70 m³ but offers a unique design and aesthetic appeal. It may be preferred by individuals who prioritize a distinctive architectural style or who are looking for a minimalist and cozy living space.
Ultimately, the selection depends on individual needs, preferences, and the intended use of the tiny house. Factors such as lifestyle, desired amenities, and personal values regarding sustainability and resource conservation should be considered when making the final decision.
for more such question on intended visit
https://brainly.com/question/31252264
#SPJ8
How do I solve this inequality?
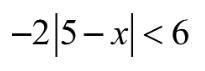
Answers
Answer:
=5
Step-by-step explanation:
6-2=5
If the right triangle's dimensions are enlarged by 3 units, the new height would be *blank* units. Just write the numerical answer.

Answers
Answer
5
Step-by-step explanation:
there are already 2 units in height therefore 2 plus 3 is 5
A pendulum is 22.9 inches long and the bob at the end of the pendulum travels 10.5 inches. Find the degree measure of the angle through which the pendulum swings
Answers
The angle which the pendulum swings is 25.78 degree.
Data;
Length of the string = 22.9indistance covered by the string = 10.5 inchesAssuming this forms a circular path, we can treat this as a right angle triangle and solve for the angle
s = rθ
\(s = r \theta\\\theta = s/r\\\theta = 10.5/22.9\\\theta = 0.45rads\)
Let's convert 0.45 rads to degree
\(0.45 * 180/\pi = 25.78^0\)
The angle which the pendulum swings is 25.78 degree.
Learn more on angular motion here;
https://brainly.com/question/6860269
Solve the following system graphically.
y < - x
y =< x - 2
Upload one solution of the system and your graph
Answers
Answer:
a solution of the system is the point that satisfies both the equations
(1, -1) is a solution of the system

Work out the surface area of the solid cuboid
L=5cm
W=2cm
H=5.3cm
Answers
Answer:
A = 94.2 cm²
Step-by-step explanation:
Given that,
Length, l = 5 cm
Width, b = 2 cm
Height, h = 5.3 cm
We need to find the surface area of the solid cuboid.
The formula for the surface area of the sold cubiod is given by :
A = 2(lb+bh+hl)
Substitute the values in the above formu;a
A = 2(5(2)+2(5.3)+(5.3)(5))
= 2(10+10.6+26.5)
= 2(47.1)
= 94.2 cm²
Hence, the required surface area is 94.2 cm².
how many permutations of length n contain at least one of the 2-cycles (12) and (34)
Answers
The total number of permutations of length n that contain at least one of the 2-cycles (12) and (34) is 2(n-2)! - (n-4)! out of n! possible permutations.
Let's first consider the total number of permutations of length n, which is given by n!.
Now, we need to count the number of permutations of length n that do not contain the 2-cycles (12) and (34). We can think of constructing such a permutation by first placing 1 in one of the n positions, then placing 2 in one of the remaining n-1 positions that is not next to 1, then placing 3 in one of the remaining n-2 positions that is not next to either 1 or 2, and so on, until we place n in the last remaining position.
The number of ways to place 1 is n, the number of ways to place 2 is n-2 (since there are n-2 positions remaining after we place 1 and one of those positions cannot be next to 1), the number of ways to place 3 is n-4 (since there are n-4 positions remaining after we place 1,2 and two of those positions cannot be next to 1 or 2), and so on. Thus, the total number of permutations of length n that do not contain the 2-cycles (12) and (34) is:
n * (n-2) * (n-4) * ... * (n-k) * ... * 3 * 1 (if n is odd)
or
(n-1) * (n-3) * ... * (n-k) * ... * 4 * 2 (if n is even)
Now, we can use the principle of inclusion-exclusion to count the number of permutations of length n that contain at least one of the 2-cycles (12) and (34). Let A be the set of permutations of length n that contain (12) and let B be the set of permutations of length n that contain (34). Then, the number of permutations of length n that contain at least one of (12) and (34) is:
|A U B| = |A| + |B| - |A intersect B|
To compute |A|, we can think of placing (12) in the first two positions, and then placing the remaining n-2 elements in the remaining n-2 positions. There are (n-2)! ways to do this, so |A| = (n-2)!. Similarly, |B| = (n-2)!.
To compute |A intersect B|, we can think of placing (12) in the first two positions and (34) in the next two positions, and then placing the remaining n-4 elements in the remaining n-4 positions. There are (n-4)! ways to do this, so |A intersect B| = (n-4)!.
Thus, the number of permutations of length n that contain at least one of (12) and (34) is:
|A U B| = (n-2)! + (n-2)! - (n-4)!
= 2(n-2)! - (n-4)!
Therefore, the total number of permutations of length n that contain at least one of the 2-cycles (12) and (34) is 2(n-2)! - (n-4)! out of n! possible permutations.
Learn more about permutations here: brainly.com/question/30649574
#SPJ4
PLEASE HELP ME:) pleaseeeee
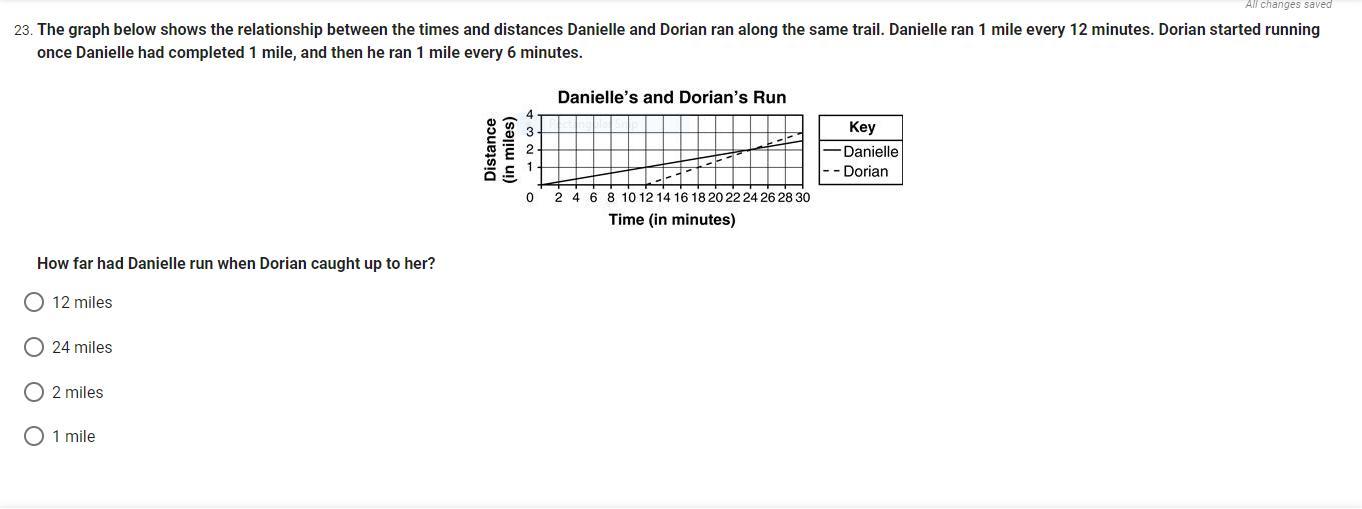
Answers
Answer:
2 miles
Step-by-step explanation:
On the graph, when Dorian caught up to Danielle, they were in the same place at the same time. This is where the solid and dashed lines on the graph intersect. Danielle is the solid line, look at the point of intersection they had both traveled 2 miles, which you can see on the vertical axis.
5 x 5^2 leaving answer in index notation
Answers
In multiplication, the exponents add up.
5.5²=5¹.5²=5³
Note:
In the extraction ,the exponents remove.
5¹⁰÷5³=5⁷
Answer:
5³
Step-by-step explanation:
Using the rule of exponents
\(a^{m}\) × \(a^{n}\) = \(a^{(m+n)}\)
Given
5 × 5²
= \(5^{1}\) × 5²
= \(5^{(1+2)}\)
= 5³ ← in index form
= [ 125 ]
help me!!
solve for d

Answers
Answer:
d =±2sqrt(7) i
Step-by-step explanation:
d^2 = -28
Take the square root of each side
sqrt(d^2) = ±sqrt(-28)
d = ±sqrt(-28)
d = ±sqrt(-1)sqrt(28)
We know that sqrt(-1) = i
d =±i*sqrt(4)sqrt(7)
d =±i 2sqrt(7)
d =±2sqrt(7) i
What is the value of I-9I?
Answers
Answer: 90
Step-by-step explanation:
91 - 1 = 90
Answer: 90
Step-by-step explanation:
An object on the moon weighs about 0.17 of what it would weigh on earth.
How much would a 185 pound astronaut weigh on the moon?
A. 3. 145 lb
B. 31.65 lb
C. 30.35 lb
D. 32.55 lb
E. 31.45 lb
Answers
All you have to do is multiply 185 by 0.17 and you get your answer, which would be E.
Based on the information given, the weight will be 31.45 lb.
From the information given, it was stated that an object on the moon weighs about 0.17 of what it would weigh on earth.
Therefore, the weight of 185 pound astronaut on the moon will be:
= 0.17 × 185
= 31.45 lb
Learn more about multiplication on:
https://brainly.com/question/19866443
Problem 2: Find a general solution for the following recurrence equation: Qn-1 +5Qn-2+3Qn-3+3". Show your work, clearly marking all steps of the solution. Hint: The characteristic polynomial factors into (x + 1)(x - 3).
Answers
The general solution of the given recurrence equation is Qn = (-1/4)(-1)n + (1/4)n(-1)n + (1/2)(3)n.
The given recurrence equation is
Qn-1 + 5Qn-2 + 3Qn-3 = 3
Let's find the characteristic equation of the given recurrence equation:
By assuming Qn = rn,
the characteristic equation can be derived as:
r3 - r2 - 5r - 3 = 0
So, the characteristic polynomial is
(r + 1)(r - 3)2
Let α = -1 and β = 3 (repeated roots)
Now, the solution of the given recurrence equation is:
Qn = Arn + Bnαn + Cnβn
As α = -1 and β = 3 are the roots of the characteristic equation, substitute these values in the above equation.
We have
A(-1)n + Bn(-1)n + Cn(3)n ... (1)
As we are going to find the general solution of Qn, the constants A, B, and C need to be determined.
Let's solve for A, B, and C by considering the first few terms of the given recurrence equation.
Suppose n = 3 in the recurrence equation Qn-1 + 5Qn-2 + 3Qn-3 = 3, we have
Q2 + 5Q1 + 3Q0 = 3 ... (2)
Now, substitute n = 2 in the general solution (1), we have
Q2 = A(-1)2 + B2(-1)2 + C23 ... (3)
Now, substitute n = 1 in the general solution (1), we have
Q1 = A(-1)1 + B1(-1)1 + C31 ... (4)
Now, substitute n = 0 in the general solution (1), we have
Q0 = A(-1)0 + B0(-1)0 + C30 ... (5)
Now, let's solve for A, B, and C using equations (2), (3), (4), and (5).
Q2 + 5Q1 + 3Q0 = 3:
2A + 5B + 3C = 3A(-1)2 + B2(-1)2 + C23:
A - B + 9C = 3A(-1)1 + B1(-1)1 + C31:
-A - B + 3C = 1A(-1)0 + B0(-1)0 + C30:
A + B + C = 1
On solving the above equations,
we get A = -1/4, B = 1/4, and C = 1/2
So, the general solution of the given recurrence equation is
Qn = (-1/4)(-1)n + (1/4)n(-1)n + (1/2)(3)n
Know more about the general solution
https://brainly.com/question/30285644
#SPJ11
Show one way that five children share
two pizzas equally
Answers
if there is 2 pizza and 5 children then 1/5 (fraction) of a pizza, or two slices, must be given to each child.
Start with two pizzas of equal size. Cut each pizza into 5 equal slices, so you have a total of 10 slices. Give each child 2 slices of pizza. Each child receives 2 slices of pizza, which is:
2/10 = 1/5 of a pizza
Each child now has 1/5 of a pizza.
Since there are 5 children, the total amount of pizza shared is:
5 × (1/5) = 1 pizza
Therefore, each child has 1/5 of a pizza, or 0.2 of a pizza.
To get the total amount of pizza that was shared, we can add up the amount of pizza each child received:
5 × (2/10) = 1 pizza
So, each child receives 2 slices of pizza, which is 1/5 of a pizza, and the total amount of pizza shared is 2 pizzas, or 1 whole pizza per 2 children.
To learn more about fraction click here
brainly.com/question/21186512
#SPJ4
The cost of admission to history museum is 3. 25$ per person over the age of 3; kids 3 and under get in for free. If the total cost of admission for the warrick family, including their two 6-month old twins, is 19. 50, find how many family members are over 3 years
Answers
There are 6 family members over 3 years old.
Let's assume that the number of family members over 3 years old is "x".
The cost of admission for each family member over 3 years old is $3.25. Since the twins are 6 months old, they are not counted in the total cost of admission. Therefore, the total cost of admission for the family, including the twins, is $19.50.
The equation representing the total cost of admission can be set up as:
3.25x = 19.50
To find the value of "x," we can divide both sides of the equation by 3.25:
x = 19.50 / 3.25
x = 6
for more such questions on cost
https://brainly.com/question/2292799
#SPJ8
HELP ASAP PLEASEEEEE
100 POINTS
An equation is shown: x2 + 4x + 4 = 0
What are the x intercepts? Show your work using a method of your choice.
What is an alternate method you could use to find the x intercepts (other than the method you used)?
What is the vertex? Is it a minimum or maximum? How do you know by looking at the equation?
What steps would you take to graph using the information you have already calculated? How would you use symmetry to help you graph?
Answers
The y-intercept is (0, 4).
An alternate method to find the x-intercepts is to factor the quadratic equation.
The vertex is (-2, 0).
The graph of the equation is illustrated below.
One of the most common types of equations is a quadratic equation, which is an equation of the form ax² + bx + c = 0. In this case, we have the equation x² + 4x + 4 = 0, and we need to find the x-intercepts.
To find the x-intercepts, we can use the quadratic formula, which is given by:
x = (-b ± √(b² - 4ac)) / 2a
where a, b, and c are the coefficients of the quadratic equation. In this case, a = 1, b = 4, and c = 4, so we can substitute these values into the formula:
x = (-4 ± √(4² - 4(1)(4))) / 2(1) x = (-4 ± √(0)) / 2 x = -2
Therefore, the x-intercept is -2. We can check this by plugging in x = -2 into the equation and verifying that it equals zero:
(-2)² + 4(-2) + 4 = 0
In this case, we can see that the equation can be factored as:
(x + 2)² = 0
Taking the square root of both sides, we get:
x + 2 = 0
x = -2
This gives us the same x-intercept as before.
To find the vertex of the parabola represented by the equation, we can use the formula:
x = -b / 2a
and then substitute this value of x into the equation to find the y-coordinate of the vertex. In this case, we have:
x = -4 / 2(1) x = -2
Substituting x = -2 into the equation, we get:
(-2)² + 4(-2) + 4 = 0
Since the coefficient of x² is positive (i.e., a = 1 > 0), the parabola opens upwards and the vertex is a minimum.
To graph the parabola, we can plot the vertex at (-2, 0) and use the x-intercept we found earlier at (-2, 0). Since the equation is symmetric about the vertical line through the vertex, we know that there is another point on the graph that is the same distance from the vertex but on the other side of the line. Therefore, we can plot the point (-3, 0) as well. We can also find the y-intercept by setting x = 0 in the equation:
0² + 4(0) + 4 = 4
Using this information, we can sketch the parabola by connecting the points (-3, 0), (-2, 0), and (0, 4), and noting that the parabola is symmetric about the line x = -2.
To know more about equation here
https://brainly.com/question/10413253
#SPJ1

Are my answers correct? Will give points if not correct can you solve please

Answers
The area of the smaller sector or minor sector is 125.66 yd².
The area of the larger sector or major sector is 326.73 yd².
What are the areas of the sector?The areas of the minor and major sectors is calculated by applying the following formulas follow;
Area of sector is given as;
A = (θ/360) x πr²
where;
r is the radius of the sectorθ is the angle of the sectorThe area of the smaller sector or minor sector is calculated as follows;
A = ( 100 / 360 ) x π ( 12 yd)²
A = 125.66 yd²
The area of the larger sector or major sector is calculated as follows;
θ = 360 - 100
θ = 260⁰
A = ( 260 / 360 ) x π ( 12 yd)²
A = 326.73 yd²
Learn more about area of sector here: https://brainly.com/question/30607726
#SPJ1
Where is the function decreasing?

Answers
Answer:
the function is decreasing at the domain values: (-∞,1)
Step-by-step explanation:
the function is decreasing in the domain values from -∞ until 1, the lowest point with no increase or decrease:
which in interval notation can be written as: (-∞,1)
I hope this helps, but if I didn't answer the question or answered wrongly I will try again.
D²y(t) + 12 Dy(t) + 36y(t) = 2 e-5t y(0) = 1, Dy(0)=0 Solve the differemtial equation using Classical Method (30pts) and Laplace Transform Method(30pts)
Answers
The solution to the differential equation D²y(t) + 12 Dy(t) + 36y(t) = 2 \(e^{(-5t)}\), with initial conditions y(0) = 1 and Dy(0) = 0, is \(y(t) = (1 + 6t) e^{(-6t)}\).
To solve the given differential equation using the classical method, we can assume a solution of the form \(y(t) = e^{(rt)}\) and find the values of r that satisfy the equation. We then use these values of r to construct the general solution.
Using the classical method:
Substitute the assumed solution \(y(t) = e^{(rt)}\) into the differential equation:
D²y(t) + 12 Dy(t) + 36y(t) = \(2 e^{(-5t)}\)
This gives the characteristic equation r² + 12r + 36 = 0.
Solve the characteristic equation for r by factoring or using the quadratic formula:
r² + 12r + 36 = (r + 6)(r + 6)
= 0
The repeated root is r = -6.
Since we have a repeated root, the general solution is y(t) = (c₁ + c₂t) \(e^{(-6t)}\)
Taking the first derivative, we get Dy(t) = c₂ \(e^{(-6t)}\)- 6(c₁ + c₂t) e^(-6t).\(e^{(-6t)}\)
Using the initial conditions y(0) = 1 and Dy(0) = 0, we can solve for c₁ and c₂:
y(0) = c₁ = 1
Dy(0) = c₂ - 6c₁ = 0
c₂ - 6(1) = 0
c₂ = 6
The particular solution is y(t) = (1 + 6t) e^(-6t).
Using the Laplace transform method:
Take the Laplace transform of both sides of the differential equation:
L{D²y(t)} + 12L{Dy(t)} + 36L{y(t)} = 2L{e^(-5t)}
s²Y(s) - sy(0) - Dy(0) + 12sY(s) - y(0) + 36Y(s) = 2/(s + 5)
Substitute the initial conditions y(0) = 1 and Dy(0) = 0:
s²Y(s) - s - 0 + 12sY(s) - 1 + 36Y(s) = 2/(s + 5)
Rearrange the equation and solve for Y(s):
(s² + 12s + 36)Y(s) = s + 1 + 2/(s + 5)
Y(s) = (s + 1 + 2/(s + 5))/(s² + 12s + 36)
Perform partial fraction decomposition on Y(s) and find the inverse Laplace transform to obtain y(t):
\(y(t) = L^{(-1)}{Y(s)}\)
Simplifying further, the solution is:
\(y(t) = (1 + 6t) e^{(-6t)\)
To know more about differential equation,
https://brainly.com/question/32622859
#SPJ11
Find the least number which when divided by 6, 15 and 18 leave remainder 5 in each case. ( pls answer fast )
Answers
Answer:
95
Step-by-step explanation:
The smallest number that divided by 6, 15, and 18 leavses 5 in each case is 95
the function f(x)=80(0.5)^ represents the distance after a pendulum begins swinging,where x is the number of swings
Answers
It looks like there may be a typo in the function you provided. It appears that you meant to write "f(x) = 80(0.5)^x", which would represent the distance after a pendulum begins swinging, where x is the number of swings.
This function indicates that the distance traveled by the pendulum decreases by half with each swing. For example, after the first swing, the distance traveled would be 80(0.5)^1 = 40 units. After the second swing, the distance traveled would be 80(0.5)^2 = 20 units. And so on.
The exponent x in the function represents the number of swings, so the distance traveled by the pendulum can be calculated by plugging in the desired value of x into the function. For example, to calculate the distance traveled after 10 swings, we can plug in x = 10:
f(10) = 80(0.5)^10 = 0.390625 units
This indicates that the pendulum has traveled a distance of approximately 0.39 units after 10 swings.
Select the correct answer.
What is the value of y in this linear system?
2x + 3y + 7z = 13
X-2y = 3
y + 4z = 1

Answers
Answer:
5 creo
Step-by-step explanation: