Answers
9514 1404 393
Answer:
y = -2·(1/2)^x
Step-by-step explanation:
The general form of the equation can be written as ...
y = a·b^x
where 'a' is the value of the y-intercept, and 'b' is the ratio of y-values for x-values that differ by 1.
From your table and graph, a = -2. From the table, ...
b = -1/-2 = 1/2
Then the exponential equation is ...
y = -2·(1/2)^x
Related Questions
hello how do I know when ratios are equivalent and when they are not?
Answers
The average age of doctors in a certain hospital is 42.0 years old with a standard deviation of 10.0 years. If 16 doctors are chosen at random for a committee, find the probability that the mean age of those doctors is less than 43.50 years. Assume that the variable is normally distributed. Group of answer choices
Answers
There is a 65.54% probability that the average age of those doctors is under 48.8 years.
What is probability?Science uses a figure called the probability of occurrence to quantify how likely an event is to occur.
It is written as a number between 0 and 1, or between 0% and 100% when represented as a percentage.
The possibility of an event occurring increases as it gets higher.
True mean = mean (or average)+/- Z*SD/sqrt (sample population)
Then,
Mean (average) = 48.0 years
The true mean must be less than 48.8 years.
SD = 6.0 years, and
Sample size (n) = 9 doctors
Using Z as the formula's subject:
Z= (True mean - mean)/(SD/sqrt (n))
Inserting values:
Z=(48.8-48.0)/(6.0/sqrt (9)) = 0.4
From the table of normal distribution probabilities:
At Z= 0.4, P(x<0.4) = 0.6554 0r 65.54%
Therefore, there is a 65.54% probability that the average age of those doctors is under 48.8 years.
Know more about probability here:
https://brainly.com/question/24756209
#SPJ1
Complete question:
The average age of doctors in a certain hospital is 48.0 years old. suppose the distribution of ages is normal and has a standard deviation of 6.0 years. if 9 doctors are chosen at random for a committee, find the probability that the average age of those doctors is less than 48.8 years. assume that the variable is normally distributed.
Hey can someone please help me out and explain the problem? Look below. Thank you! I’ll give brainly

Answers
A population mean is normally distributed with a mean of 56 and a standard deviation of 12.

Answers
The mean of the sampling distribution (p) and The standard error of the mean (o) are 56 and 2 respectively.
What is normal distribution?A probability distribution that is symmetric about the mean is the normal distribution, sometimes referred to as the Gaussian distribution. It demonstrates that data that are close to the mean occur more frequently than data that are far from the mean.
According to question:(a) The mean of the sampling distribution (p) is equal to the population mean, which is 56.
(b) The standard error of the mean (o) is calculated as the standard deviation of the population divided by the square root of the sample size. So for a sample of 36 participants:
o = 12 / √36 = 2
(c) The distribution of the sample means (p) will be approximately normal with a mean of 56 and a standard deviation of 2. To sketch this distribution with M ± 3 SEM, we would plot a normal distribution with mean 56 and standard deviation 2, and shade the region that is 3 standard errors away from the mean on either side.
This region would capture approximately 99.7% of the data if the samples were selected randomly and independently from the population.
To know more about Normal distribution visit:
brainly.com/question/29509087
#SPJ1
1. The slant height of a cone is 5cm and the radius of its base is 3cm. Find correct to the nearest
whole number the volume of the cone (A) 48cm3 (B) 47cm3 (C) 38cm3 (D)13cm3
Answers
The volume of the cone is 13 cm³. option D
How to determine the volumeTo determine the volume of the cone, we have that;
The formula for calculating the volume of a cone is expressed as;
Volume = (1/3)πr ²√(L ² - r ²).
Such that;
r is the radiusL is the slant heightSubstitute the values, we have;
Volume = 1/3 × 3.14 ² × √(25 - 9)
Find the squares, we get;
Volume, V = 1/3 × 9. 86 × √16
Find the square root
Volume, V = 1/3 × 9.86 × 4
Volume, V = 13 cm³
Learn more about volume at:
#SPJ1
A constant function has the form f(x) = c and has the domain of all real numbers with a range consisting of a single real number c.
Answers
The domain of a function f(x) is the set of all values for which the function is defined, and the range of the function is the set of all values that f takes.
A constant function is a linear function whose range contains only one element irrespective of the number of elements of the domain.
Since a constant function is defined for all real values of x, then we have that:
1) Its domain is the set of all real numbers, and
2) Since a constant function f(x) = c leads to only one output, which is k, its range is the set with just one element c.
Therefore,
\(\begin{gathered} domain=\mathfrak{\Re } \\ range=c \end{gathered}\)The statement is TRUE.
MODELING REAL LIFE
The height of a tree trunk is 20 meters and the base diameter is 0.5 meter.
a. The wood has a density of 380 kilograms per cubic meter. Find the mass of the trunk.
The mass of the tree trunk is about
kilograms.
Question 2
b. For each of the next 5 years, the trunk puts on a growth ring 4 millimeters thick. In the first year, the height increases by 0.2 meter. The tree produces the same amount of wood each year. What is the height of the trunk after 5 years?
The height of the trunk is about
meters after 5 years.
Answers
Answer:
a. 1492 kg
b. 20.8 m
Step-by-step explanation:
Given a tree is initially 20 m high and has a diameter of 0.5 m, you want the mass of the trunk if its density is 380 kg/m³. If it adds a growth ring of 4 mm per year and adds height of 0.2 m in the first year, you want the height of the tree after 5 years, assuming the same amount of wood is added each year.
a. MassThe volume of the tree trunk is that of a cylinder. The formula is ...
V = (π/4)d²h
V = (π/4)(0.5 m)²(20 m) ≈ 3.9270 m³
The mass is the product of volume and density:
M = Vρ
M = (3.9270 m³)(380 kg/m³) ≈ 1492 kg
The mass of the tree trunk is about 1492 kg.
b. HeightIn the first year, the diameter of the tree increases by 8 mm, and the height increases by 0.2 m,. This means the volume of the tree increases to ...
V = (π/4)(0.508 m)²(20.2 m) ≈ 4.0942 m³
The volume increase is the same each year for 5 years, so after 5 years, the volume is ...
3.9270 m³ + 5(4.0942 -3.9270) m³ ≈ 4.7630 m³
At that time, the diameter is about 0.540 m. Solving the volume equation for the height, we find it to be ...
h = 4v/(π·d²)
h = 4(4.7630 m³)/(π·(0.54 m)²) ≈ 20.797 m
The height of the trunk after 5 years is about 20.8 m.
__
Additional comment
We note that the wood added in the first year includes the cylindrical shell represented by the tree ring, and a cylindrical "plug" that is 0.2 m high and equivalent in diameter to the rest of the tree. This seems an odd way for the tree to grow, but may be a reasonable approximation to the actual growth.
The height, diameter, and growth are all given to 1 significant figure. Hence the 4- and 3-significant figures used in the answers may be unsupported by the precision of the given numbers. Keeping 2 significant figures, we might report the initial mass as 1500 kg, and the final height as 21 m.
The graph is drawn by a function formulated to have the correct height at the x-intercept: v(d, h) - (final volume) = 0.
<95141404393>

Help help please please
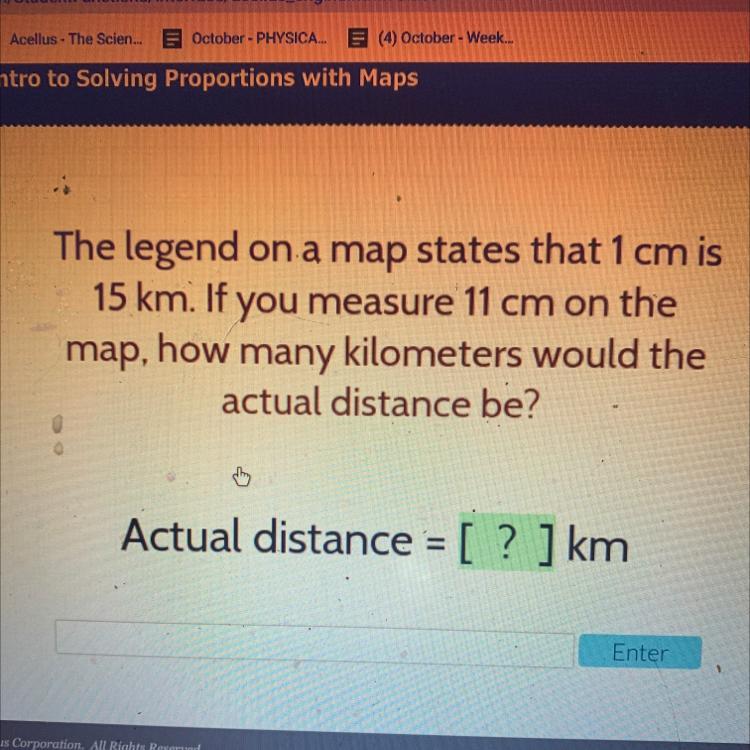
Answers
Answer:
165km
Step-by-step explanation:
if 1cm on the map = 15km,
then since 11cm is 11x 1, we multiply the kilometers by 11, getting 165km.
What is the inverse of each statement below: Be sure to label your
answers as a, b, c, and d.
a.) Add 25
b.) Divide -18
c.) Subtract 3
d.) Multiply 14
Answers
The term “inverse” in mathematics generally refers to an operation that undoes or reverses another operation. However, the phrase "inverse of maths tools" doesn't really make sense because “maths tools” is not a specific mathematical operation.
What is the inverse of maths tools?Mathematical tools can refer to various instruments or techniques used in mathematics, such as calculators, rulers, compasses, graph paper, software, etc. Each of these tools has its own purpose and may or may not have an inverse operation or tool associated with it.
For example, the inverse of addition is subtraction, the inverse of multiplication is division, and the inverse of differentiation is integration. However, it's not clear what the inverse of a “maths tool” would be.
Therefore, a) The inverse of “Add 25” would be “Subtract 25.”What is the b) The inverse of “Divide -18” would be “Multiply -18.” c) The inverse of “Subtract 3” would be “Add 3.” d) The inverse of “Multiply 14” would be “Divide 14.”
Learn more about inverse here:
https://brainly.com/question/30659571
#SPJ1
No links pls
which inequality is true
A. π - 3 > 1
B. 9/3π > 1
C. π + 7 < 10
D. 9π > 27
Answers
Answer:
D.) 9*pi >27
Step-by-step explanation:
9*pi = 28.2743338823...
28.2743338823... > 27
D.) 9*pi > 27 = True
Regards!
Answer:
It’s d hope you get it right
Given the geometric sequence an with the following information, find a7.

Answers
To find the value of Az in the geometric sequence, we can use the given information. The geometric sequence is represented as follows: A3, 60, 160, 06 = 9.
From this, we can see that the third term (A3) is 60 and the common ratio (r) is 160/60.
To find Az, we need to determine the value of the nth term in the sequence. In this case, we are looking for the term with the value 9.
We can use the formula for the nth term of a geometric sequence:
An = A1 * r^(n-1)
In this formula, An represents the nth term, A1 is the first term, r is the common ratio, and n is the position of the term we are trying to find.
Since we know A3 and the common ratio, we can substitute these values into the formula:
60 =\(A1 * (160/60)^(3-1)\)
Simplifying this equation, we have:
\(60 = A1 * (8/3)^260 = A1 * (64/9)\)
To isolate A1, we divide both sides of the equation by (64/9):
A1 = 60 / (64/9)
Simplifying further, we have:
A1 = 540/64 = 67.5/8.
Therefore, the first term of the sequence (A1) is 67.5/8.
Now that we know A1 and the common ratio, we can find Az using the formula:
Az = A1 * r^(z-1)
Substituting the values, we have:
Az =\((67.5/8) * (160/60)^(z-1)\)
However, we now have the formula to calculate it once we know the position z in the sequence.
For more such questions on geometric sequence
https://brainly.com/question/24643676
#SPJ8
What’s the formula for the series -5,10,-20,40
Answers
Answer:
Stare at it long enough. You will notice that with each step you double the value, and change sign. It makes it a geometric sequence of ratio -2. At this point you have two ways of writing down:
Option 1: Ricorsively, the first term is -5, then the next term is -2 times the previous one:
\(\left \{ {{a_0=-5} \atop {a_{n+1}=-2a_n}} \right.\)
Option 2: In closed form, remembering that the n-th term in a geometric sequence is the starting term times the n-th power of the ratio:
\(a_n=-5 (-2)^n\)
Either work, depending on what you need to use it for.
Which unit of measure is the most reasonable to use to estimate the weight of a newborn baby?
Select one:
A. tons
B. ounces
C. pounds
D. None of these
Answers
Answer:
C.
Step-by-step explanation:
I think it is C. because tons are way too much (there are 32,000 ounces in a ton) and there are only 16 ounces in a pound. An average baby is about 17.5 pounds at birth, or 17 pounds and 8 ounces.
hope this helped!
If quadrilateral A’B’C’D’ = DK (ABCD), which of the following statements are true?
Select all that apply. (Hint: Draw a picture)
The quadrilaterals ABCD and A'B'C'D' are congruent only if k = 1.
The quadrilaterals ABCD and A'B'C'D' are similar only if k ≥ 1.
The corresponding side lengths are related by AB = k(A'B')
The corresponding side lengths are related by k(CB) = C'B'.

Answers
Answer:
The quadrilaterals ABCD and A'B'C'D' are congruent only if k = 1.
The corresponding side lengths are related by k(CB) = C'B'.
Step-by-step explanation:
Transformation is the movement of a point from its initial location to a new location. Types of transformation are rotation, reflection, translation and dilation.
Dilation is the increase or decrease in size of a figure by a factor k. If k > 1, the figure is increased, if k < 1, the figure is reduced and if k = 1, the figure does not changes shape. The image of an dilated figure is similar to the original image.
a) If k = 1, then the resulting image produced by dilating ABCD is congruent. Hence, The quadrilaterals ABCD and A'B'C'D' are congruent only if k = 1.
b) Dilation produce image similar to the original figure, hence quadrilaterals ABCD and A'B'C'D' are similar only if k ≥ 1 and k < 1.
c) Since ABCD is dilated by a factor of k to produce A'B'C'D', hence A'B' = k(AB).
d) C'B' = k(CB)
Which triangle is △ABC similar to and why?
Answers
Answer:
can we get a picture
Step-by-step explanation:
what plus what plus what is equal to 30 and all the numbers must be odd
Answers
Answer:
1 + 29
3 + 27
5 + 25
7 + 23
9 + 21
11 + 19
13 + 17
15 + 15
~theLocoCoco
Coordinate grid shows from -2 to positive two on x-axis and -2 to positive two on y-axis. There are increments I have one over four for each grid line on each of the two axes. Only the whole numbers are labeled on either side of the axis. A point A is shown at the intersection of 5 grid lines to the right of the y-axis and 3 grid lines below the x-axis. What are the coordinates of point A?
Answers
The coordinates of point A are ( 5/4, -3/4)
What are coordinates?
A pair of numbers that use the separations between the two reference axes to define the location of a point on a coordinate plane. usually represented by the x- and y-values, respectively, (x, y).
The position of a point or a shape in a given space is determined by coordinates, which are numbers (a map or a graph ).
x - coordinate = 5 grid lines to the right of the y-axis
y - coordinate = 3 grid lines below the x-axis.
The point A is in the 4th quadrant
(x,y) = ( + 5 grid lines, -3 grid lines )
There are increments I have one over four for each grid line on each of the two axes
This means,
(x,y) = ( + 5 * 1/4, -3*1/4 ) = ( 5/4, -3/4)
So, the coordinates of point A are ( 5/4, -3/4)
To learn more about the coordinates from the given link
https://brainly.com/question/17206319
#SPJ1
We consider the differences between the reading and writing scores of a random sample of 200 students who took the High School and Beyond Survey. The mean and standard deviation of the differences are −0.556 and 8.871 points.
Requried:
a. Calculate a 95% confidence interval for the average difference between the reading and writing scores of all students.
b. Interpret this interval in context. (Round your answers to two decimal places.)
Answers
Answer:
A) True : Confidence Interval is the interval range around sample statistic, which is certain by extent of confidence level, to consist the actual population parameter.
B) True : Confidence Interval is the interval range around sample statistic, which is certain by extent of confidence level, to consist the actual population parameter.
C) False : Null Hypothesis can be accepted, despite of being actually false. This is called Type 2 Error.
Step-by-step explanation:
Hope this helps:)
Instructions for a chemical procedure state to mix salt, baking soda, and water in a 12:22:12 ratio by mass. How many grams of baking soda would be required to make a mixture that contains 30 grams of water?
Answers
Answer:
To determine the amount of baking soda needed, we need to use the given ratio to calculate the masses of salt, baking soda, and water required to make the mixture.
The total mass of the mixture is 12 + 22 + 12 = 46 parts. This means that for every 46 grams of the mixture, there are 12 grams of salt, 22 grams of baking soda, and 12 grams of water.
To find out how much baking soda is needed for 30 grams of water, we can use a proportion:
12 grams water / 46 grams mixture = 30 grams water / x grams mixture
where x is the mass of the mixture needed to obtain 30 grams of water.
Cross-multiplying, we get:
12 grams water * x grams mixture = 30 grams water * 46 grams mixture
Simplifying:
x grams mixture = (30 grams water * 46 grams mixture) / 12 grams water
x grams mixture = 115 grams mixture
Therefore, to make a mixture containing 30 grams of water, we need a total mixture mass of 115 grams. Using the given ratio, we know that for every 46 grams of the mixture, we need 22 grams of baking soda.
So, for a 115-gram mixture, we can calculate the amount of baking soda needed:
22 grams baking soda / 46 grams mixture = y grams baking soda / 115 grams mixture
where y is the mass of baking soda needed.
Cross-multiplying, we get:
22 grams baking soda * 115 grams mixture = 46 grams mixture * y grams baking soda
Simplifying:
y grams baking soda = (22 grams baking soda * 115 grams mixture) / 46 grams mixture
y grams baking soda = 55 grams baking soda (rounded to two decimal places)
Therefore, to make a mixture containing 30 grams of water using the 12:22:12 ratio, we need 55 grams of baking soda.
Step-by-step explanation:
pls mark brainlist!
Given m/8= 86° and m/4= (4x + 2)°, what is the value of x ?
X =

Answers
Bring the variable to the left and the remaining values to the right to define the value of x. If m/8 = 86° and m/4 = (4x + 2)° then value of x = 21.
How to find the value of x?Any of the algebraic expressions, including addition, subtraction, multiplication, and division, should be used. Bring the variable to the left and the remaining values to the right to determine the value of x. To determine the outcome, simplify the values.
Let the m/8 = 86° and m/4 = (4x + 2)°
m ∠4 = m ∠8 (Corresponding angles are equal)
To estimate the value of x
4x + 2 = 86
Substracting both sides of the equation by 2, we get
4x + 2 - 2 = 86 - 2
simplifying the above equation,
4x = 86 - 2
4x = 84
Dividing both sides of the equation by 4, we get
4x / 4 = 84 / 4
x = 21
Therefore, the value of x = 21.
To learn more about the value of x refer to:
https://brainly.com/question/28032673
#SPJ13
Find the length of the line joining A (3,5) and B (1,3)
Answers
Answer:
2√2 units.
Step-by-step explanation:
To find the length of the line joining points A(3, 5) and B(1, 3), we can use the distance formula. The distance formula is given by:
d = sqrt((x2 - x1)^2 + (y2 - y1)^2)
Substituting the coordinates of points A and B into the formula, we have:
d = sqrt((1 - 3)^2 + (3 - 5)^2)
= sqrt((-2)^2 + (-2)^2)
= sqrt(4 + 4)
= sqrt(8)
= 2sqrt(2)
Therefore, the length of the line joining points A and B is 2√2 units.
A total of 27 students are in your class. There are nine more males than females.
How many females are in your class?
Answers
find the length of the side (x)

Answers
Answer:
C) x = 3.7
Step-by-step explanation:
sin 41° = x/5.6
0.6561 = x/5.6
x = 3.7
What is the value of g1(-2)

Answers
Answer:
look at it
Step-by-step explanation:
hope its help
please follow

PLEASE HELP ME IM RUNNING OUT OF TIME
The graph of a linear function is shown.
Which word describes the slope of the line?
A. positive
B. negative
C. zero
D. undefined

Answers
Answer:
negative
Step-by-step explanation:
its below the negative mark and its not verticle so it can't be undefined
Paxton invests $4850 at 7.6%/a simple interest. If she wants the money to increase to $8000, how long will she need to invest her money?
Answers
Therefore, Paxton will need to invest her money for approximately 21.62 years to increase her investment from $4850 to $8000 at a simple interest rate of 7.6% per year.
To determine how long Paxton needs to invest her money in order for it to increase to $8000, we can use the formula for simple interest:
I = P * r * t
Where:
I = Interest earned
P = Principal (initial investment)
r = Interest rate per year (expressed as a decimal)
t = Time (in years)
Given that Paxton invests $4850 at an interest rate of 7.6% per year, we have:
4850 * 0.076 * t = 8000
Simplifying the equation:
369.8t = 8000
To find t, we divide both sides of the equation by 369.8:
t ≈ 8000 / 369.8 ≈ 21.62 years
For such more question on interest rate
https://brainly.com/question/29451175
#SPJ8
PLS HELP ASAP, THANK YOU
PS. WILL MARK BRAINLIEST

Answers
i am so sorry me dont know
Answer:
Answer: Composite figure: 360 ft3
Explanation:
The volume of the triangular prism:
The base area of the prism = 1/2 x 4 x 6 = 12 ft2
Height = 6 ft
The volume of the triangular prism = 12 x 6 = 72 ft3
The volume of the rectangular prism:
The base area of the prism = 4 x 6 = 24 ft2
Height = 12 ft
The volume of the triangular prism = 12 x 24 = 288 ft3
Volume of the composite figure = (288 + 72)ft3 = 360 ft3
Step-by-step explanation:
ground casket, shadow 16 inches long. What would be the distance from the top of the yardstick to the edge its shadow
Answers
Using the proportion formula, the height of the building is obtained as 40 meters.
What is proportion?
In general, the term "proportion" refers to a part, share, or amount that is compared to a whole. According to the definition of proportion, two ratios are in proportion when they are equal.
We can use proportions to solve the problem.
The ratio of the height of the pole to its shadow is the same as the ratio of the height of the building to its shadow.
That is -
height of pole / length of pole's shadow = height of building / length of building's shadow
Substituting the given values in the equation -
16 / 10 = height of building / 25
To find the height of the building, we can cross-multiply and solve for it -
16 x 25 = 10 × height of building
400 = 10 × height of building
height of building = 400 / 10
height of building = 40 meters
Therefore, the height of the building is 40 meters.
To learn more about proportion from the given link
https://brainly.com/question/19994681
#SPJ1
A 16 meter pole casts a 10 meter long shadow. If at the same time of the day, a building casts a shadow of 25 meters, what is the height of the building?
Simplify the expression:
3x+b+p^2
Answers
Answer:
\(3x+b+p^2\) is already simplified
Step-by-step explanation:
\(3x+b+p^2\) is already simplified
Answer:
The equation is already simplified
Step-by-step explanation:
Nothing fuurther can be done to this equation
Find the greatest common factor of 14 and 16
Answers
Answer:
the answer is 2
Step-by-step explanation:
Answer:
Step-by-step explanation:
It is 2, because it is the only factor that can go with both of the numbers.
