Please help math is my weakest subject and I have no idea what to do I’ll give brainliest!!!!

Answers
Using translation concepts, we have that:
The vertex of the parent function is (0,0).The vertex of the new function is at (-3,-1).a = -0.5.b = 0.h = -3.k = -1.What is a translation?A translation is represented by a change in the function graph, according to operations such as multiplication or sum/subtraction either in it’s definition or in it’s domain. Examples are shift left/right or bottom/up, vertical or horizontal stretching or compression, and reflections over the x-axis or the y-axis.
The parent absolute value function is defined by:
f(x) = |x|.
And has vertex at (0,0).
After a translation, the absolute value function is given by:
g(x) = |a(x - h)| + k.
The vertex is at: (h, k).
In this problem, the function is:
g(x) = |-0.5(x + 3)| - 1.
Hence:
The vertex of the new function is at (-3,-1).a = -0.5.b = 0.h = -3.k = -1.More can be learned about translation concepts at https://brainly.com/question/4521517
#SPJ1
Related Questions
Suppose that the x-intercepts of the graph of y = f(x) are -5 and 3. . a) What are the x-intercepts of the graph of y = 7f(x)?
Answers
Answer:
\((-5)\) and \(3\).
Step-by-step explanation:
The \(x\)-intercepts of a graph refer to points where the graph intersects the \(x\!\)-axis. These are \(x\!\!\) values for which \(f(x) = 0\).
For example, since \(x = (-5)\) is one of the \(x\)-intercepts of \(y = f(x)\), it must be true that \(f(-5) = 0\). Likewise, since \(3\) is one of the \(x\)-intercepts of \(y = f(x)\!\), \(f(3) = 0\).
Since \(f(-5) = 0\), the expression \(7\, f(-5)\) would also evaluate to \(0\) (that is, \(7\, f(-5) = (7)\, (0) = 0\).) Thus, \(x = (-5)\) would be an \(x\)-intercept of the new graph \(y = 7\, f(x)\).
Likewise, since \(f(3) = 0\), \(7\, f(3) = (7)\, (0) = 0\), such that \(x = 3\) would also be an \(x\)-intercept of the new graph \(y = 7\, f(x)\).
No other points could be an \(x\)-intercept of the new graph \(y = 7\, f(x)\) without being an \(x\!\)-intercept of \(y = f(x)\). For example, assume that \(x = x_{0}\) is an \(x\)-intercept of \(y = 7\, f(x)\) but not \(y = f(x)\). \(7\, f(x_{0}) = 0\), such that \(f(x_{0}) = (1/7)\, (7\, f(x_{0})) = (1/7)\, (0) = 0\)- contradiction.
Therefore, the \(x\)-intercepts of the new graph would be \(x = (-5)\) and \(x = 3\).
To graph the inequality y < 2x - 1, you would draw a solid line. A true B false
Answers
Hope it helps : )
True
Personally, when I see the line underneath the equality sign, I know I've got to draw a dotted line. That's how I remember the difference between drawing a solid / dotted line.
Hope this helps!
Find f(-2) for the
piece-wise function.
f(x) =
X
|x+
x+1
if x ≤ 0
if x > 0
f(-2)=[?]
![Find f(-2) for thepiece-wise function.f(x) =X|x+x+1if x 0if x > 0f(-2)=[?]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/Zkhp21lJP8qF5ciFEYtRX4TO4cpBz1kP.png)
Answers
Answer:
The answer is,
f(-2) = -2
Step-by-step explanation:
Since -2 < 0, and f(x) = x for x < 0,
so we get,
f(-2) = -2
At the party, Max wants each balloon to
have a string that is 100 centimeters long.
The string he wants to buy comes in rolls of
25 meters. How many rolls of string does
Max need to buy if he plans to have 50
balloons at the party?
Hellp me with this
Answers
Max needs to buy two rolls of string, hopefully this helped :)
x2 + 4x - 9 = 5x + 3
O A. 4
O B. -3
O C. -7
O D. 5
E. -2
F-4
Answers
Answer:
\( {x}^{2} + 4x - 9 = 5x + 3 \\ {x }^{2} - x - 12 \\ {x}^{2} - 4x + 3x - 12 \\ x(x - 4) + 3(x - 4) \\ (x - 4)(x + 3) \\ x = 4 \: and - 3\)
show that the volume of the unit cube is one
Answers
Check the picture below.

Please answer these 2 word problems for BRAINLIEST AND IF CORRECT I WILL GIVE EXTRA POINTS

Answers
Answer:
150
Step-by-step explanation:
What is the area of this triangle?
150 cm²
210 cm²
315 cm²
420 cm²

Answers
Answer:
\(area = \frac{1}{2} (base)(height) \\ area = \frac{1}{2} (35cm)(12cm) \\ area = \frac{1}{2} (420 {cm}^{2} ) \\ area = 210 \: {cm}^{2} \)
The area of the triangle with height 12 cm and base 35 cm is A = 210 cm²
What is a Triangle?A triangle is a plane figure or polygon with three sides and three angles.
A Triangle has three vertices and the sum of the interior angles add up to 180°
Let the Triangle be ΔABC , such that
∠A + ∠B + ∠C = 180°
The area of the triangle = ( 1/2 ) x Length x Base
For a right angle triangle
From the Pythagoras Theorem , The hypotenuse² = base² + height²
if a² + b² = c² , it is a right triangle
if a² + b² < c² , it is an obtuse triangle
if a² + b² > c² , it is an acute triangle
Given data ,
Let the triangle be represented as ΔABC
Now , the base of the triangle is AB = 35 cm
The height of the triangle is BC = 12 cm
And , the area of the triangle = ( 1/2 ) x Length x Base
On simplifying , we get
Area of the triangle A = ( 1/2 ) x 12 x 35
Area of the triangle A = ( 6 x 35 )
Area of the triangle A = 210 cm²
Hence , the area of the triangle is 210 cm²
To learn more about triangle click :
https://brainly.com/question/16739377
#SPJ3
double the sum of a number and 3
Answers
Hey there!
Your answer is 2(n + 3)
"Double" represents multiplying by two. Also, "sum of a number and 3" represents the addition of 3 and a number, so we could put "n + 3". Since we are doubling the sum, it would be "2(n + 3)"
Have a terrificly amazing day! :D
Explanation:
Sum= +
Twice= multiply
So, you find the sum and multiply it by 2
Next anyone help it always helps haha 20 points

Answers
Answer:
Distance between Amber and Claire's house = 17.63 blocks
Step-by-step explanation:
In this graph three points are showing the locations of Amber's, Betsey's and Claire's houses.
Each unit on the graph represents 1 block.
Amber walks from her house to Claire's house, then on to Betsey's house.
We have to calculate the distance covered by Amber.
Since Distance from Claire's house to Betsey's house = 7 blocks = 7 units
and distance between Amber and Betsey's house = 8 blocks = 8 units
Now we will calculate the distance between Amber and Claire's house by Pythagoras theorem.
Distance² = 7² + 8² = 49 + 64 = 113
Distance = √113 units = 10.63 units
Therefore, total distance walked by Amber = 10.63 + 7 = 17.63 units = 17.63 blocks
Answer:
the answer might be 17. 63 because there are 7 blocks in between them so try that sorry if its wrong
find the slope of the tangent line to the curve y at x. then write the equation of this tangent line. question content area bottom part 1 the slope of the line tangent to the curve y at x is 36. part 2 the equation of the line tangent to the curve y at x is y minus y equals 36 (x minus 3 ).
Answers
the equation of the line tangent to the curve y at x = 3 is y = 36x - 102. The slope of the tangent line to the curve y at x = 3 is 36.
The equation of the line tangent to the curve y at x = 3 can be written using the point-slope form of a line, which is:
y - y1 = m(x - x1)
where m is the slope of the line, (x1, y1) is a point on the line, and m and (x1, y1) are known. In this case, m = 36 and (x1, y1) = (3, y). Substituting these values into the equation above, we get:
y - y = 36(x - 3)
y = 36x - 102
So the equation of the line tangent to the curve y at x = 3 is
y = 36x - 102.
To know more Tangent
https://brainly.com/question/4470346
#SPJ4
Help pls I will give brainliest

Answers
Answer:
12cm
Step-by-step explanation:
This is a problem which can be solved with the pythagoras therom.
\(a^{2} +b^{2} =c^{2}\)
Plus we can split this triangle into two triangles.
The split triangle has dimensions of 13(bc) by 5 cm(dc).\(a^{2} +b^{2} =c^{2}\)
\(5^{2} +b^{2} =13^{2}\)
Now we solve for b which is the lenght of bd
\(25 +b^{2} =169\)
\(b^{2} =144\)
\(b = \sqrt{144}\)
\(b = 12\)
Therefore the lenght of bd is 12cm
Hope this helps! :)
To start, you can see that this is a large triangle divided in half to create 2 right triangles. This means we can use the Pythagorean theorem (a^2) + (b^2) = (c^2) to find the segment bd.
To use the theorem we must know at least 2 values of the sides of the triangle. Since segment ac = 10 cm, we can divide this by 2 to get the base values of the smaller triangles, which would be 5 cm.
So a = 5 cm, c = 13 cm
Now, we have what we need and we can plug it in to the equation:
(5 cm)^2 + b^2 = (13 cm)^2
25 cm + b^2 = 169
b^2 = 144
b = 12 cm
Every month Jordan puts $14 into her bank account. Her grandma puts additional money into Jordan's bank account every month. After 12 months, Jordan has $216 in her bank account. The equation
below can be used to determine x, the amount of money her grandma adds each month
How much did Jordan's grandma put into the account each month?
A
$4.00
B
$16.83
$17.45
D
$48.00
Answers
Answer
D $48.00 u need to multiply 216 and 12 to get 48
help!!! Choose the product . - 6p ^ 3 * (3p ^ 2 + 5p - 1)
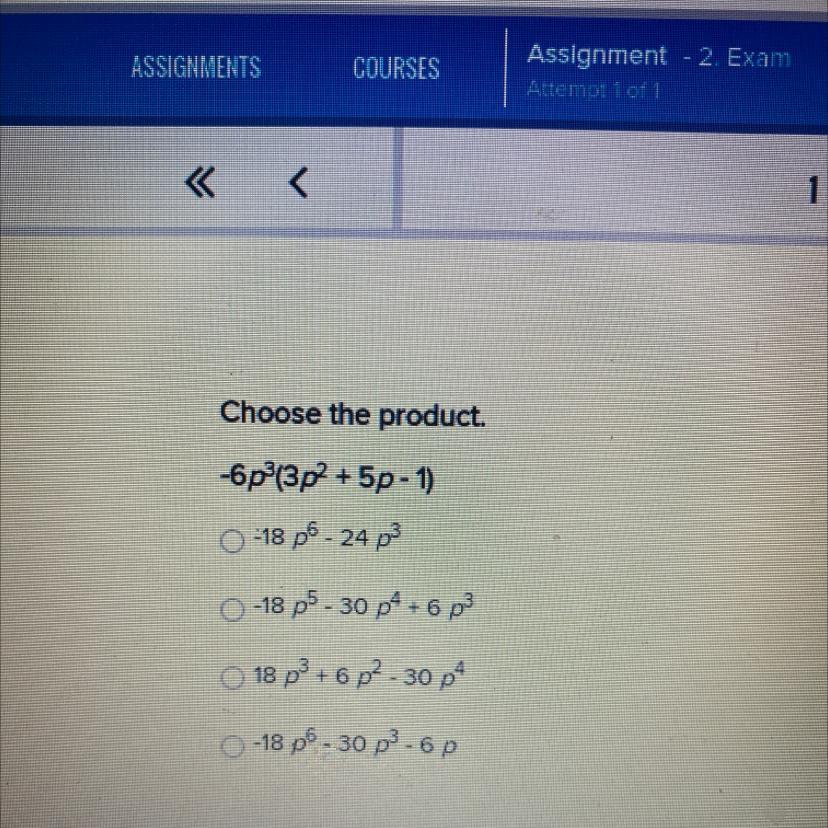
Answers
Answer:
\(-18p^{5} -30p^{4} +6p^{3}\)
Step-by-step explanation:
\((-6p^{3} )(3p^2+5p-1)\)
\((-6p^3)(3p^2)+(-6p^3)(5p)+(-6p^3)(-1)\)
\(-18p^{5} -30p^{4} +6p^{3}\)
hope this helps.....
PLEASE HELP! WILL GIVE BRAINLIEST!
1. for a party, the family bought 24 pizzas for $12.50 each and 36 bottles of soda for $1.20 each. how much did the family spend on pizza? fill in the blank with the numerical answer only. the family spent $_______ on pizza.
2. for a party, the family bought 24 pizzas for $12.50 each and 36 bottles of soda for $1.20 each. how much did the family spend on soda? fill in the blank with the numerical answer only. the family spent $_______ on soda.
3. for a party, the family bought 24 pizzas for $12.50 each and 36 bottles of soda for $1.20 each. how much did the family spend in all? fill in the blank with the numerical answer only. the family spent $_______ in all.
Answers
Answer:
Step-by-step explanation: for a party, the family bought 24 pizzas for $12.50 each and 36 bottles of soda for $1.20 each. how much did the family spend on pizza? fill in the blank with the numerical answer only. the family spent $_______ on pizza.
The family spent 300$ on pizza
Answer:
Answer
Step-by-step explanation:
for pizza: $300.00
for soda: $43.20
In all: 343.20
A tin can has dimensions 2m ×1.5m×1m high. How many litres of kerosene oil can it hold?
Answers
Answer:
3000 liters
Step-by-step explanation:
To calculate the volume of the tin can, we can multiply its dimensions:
Volume = 2m × 1.5m × 1m = 3 cubic meters
Since a liter is equivalent to 0.001 cubic meters, we can convert the volume of the tin can to liters:
Volume (in liters) = 3 cubic meters × 1000 liters/cubic meter = 3000 liters
Therefore, the tin can can hold 3000 liters of kerosene oil.
Aɳʂɯҽɾҽԃ Ⴆყ ɠσԃKEY ꦿ
Identify the algebraic rule that would translate a figure 3 units left and 2 units up.

Answers
The algebraic rule for translating the figure 3 units left and 2 units up is (x-3, y+2). Option B.
To translate a figure 3 units to the left and 2 units up, we need to adjust the coordinates of the figure accordingly. The algebraic rule that represents this translation can be determined by examining the changes in the x and y coordinates.
When we move a figure to the left, we subtract a certain value from the x coordinates. In this case, we want to move the figure 3 units to the left, so we subtract 3 from the x coordinates.
Similarly, when we move a figure up, we add a certain value to the y coordinates. In this case, we want to move the figure 2 units up, so we add 2 to the y coordinates.
Taking these changes into account, we can conclude that the algebraic rule for translating the figure 3 units left and 2 units up is (x-3, y+2). The x coordinates are shifted by subtracting 3, and the y coordinates are shifted by adding 2. SO Option B is correct.
For more question on algebraic visit:
https://brainly.com/question/30652385
#SPJ8
Assume the average nightly payroll for a city’s downtown restaurants on the weekend is $2200 with a standard deviation of $300. The distribution has a bell-shaped curve. A manager wants to be 99% sure he has this cost covered for the next four weeks and puts away $10,000. Will he have enough? Use your z-score formula result to justify your answer. Please respond with the dollar amount and round to the nearest dollar.
Hint: Round your z-value to the hundredths place and direction of the graph will matter.
Answers
Given statement solution is :- The manager will have enough funds, and the amount set aside ($10,000) is sufficient to cover the payroll for the next four weeks.
To determine if the manager will have enough funds to cover the nightly payroll for the next four weeks, we need to calculate the total cost for four weeks and compare it to the amount set aside.
The nightly payroll has a mean of $2200 and a standard deviation of $300. Since there are seven nights in a week, the weekly payroll can be calculated as:
Weekly Payroll = Nightly Payroll * Number of Nights in a Week
= $2200 * 7
= $15,400
To calculate the total cost for four weeks, we multiply the weekly payroll by four:
Total Cost for Four Weeks = Weekly Payroll * Number of Weeks
= $15,400 * 4
= $61,600
Now, let's calculate the z-score using the formula:
z = (X - μ) / σ
Where:
X = Total Cost for Four Weeks
μ = Mean of the distribution
σ = Standard deviation of the distribution
z = ($61,600 - $2200) / $300
z = $59,400 / $300
z ≈ 198
To determine if the manager will have enough funds to cover the payroll, we need to find the proportion of the distribution that is less than or equal to the z-score. This can be done by consulting a standard normal distribution table or using statistical software.
For a z-score of 198, the proportion in the tail of the distribution is essentially 1 (or 100%). This means that the manager is virtually guaranteed to have enough funds to cover the payroll for the next four weeks.
Since the manager has set aside $10,000, which is less than the calculated total cost of $61,600, he will indeed have enough funds to cover the payroll.
Therefore, the manager will have enough funds, and the amount set aside ($10,000) is sufficient to cover the payroll for the next four weeks.
For such more questions on Funds Cover Payroll: Confirmed
https://brainly.com/question/32039603
#SPJ8
A shipping box is 36 inches by 24 inches by 18 inches
how many cubic feet can it hold
Answers
Answer:
To find the volume of the shipping box in cubic feet, we need to convert the dimensions from inches to feet and then calculate the volume.
Given:
Length = 36 inches
Width = 24 inches
Height = 18 inches
Converting the dimensions to feet:
Length = 36 inches / 12 inches/foot = 3 feet
Width = 24 inches / 12 inches/foot = 2 feet
Height = 18 inches / 12 inches/foot = 1.5 feet
Now, we can calculate the volume of the box by multiplying the length, width, and height:
Volume = Length * Width * Height
Volume = 3 feet * 2 feet * 1.5 feet
Volume = 9 cubic feet
Therefore, the shipping box can hold 9 cubic feet.
Step-by-step explanation:
First convert the units because it's asking for the cubic feet but they give us the measurements in inches.
To convert inches to feet we divide the number by 12.
36 ÷ 12 = 3
24 ÷ 12 = 2
18 ÷ 12 = 1.5
Now to find the volume, we multiply it all together.
3 × 2 × 1.5 = 9
It can hold 9 cubic feet.
Hope this helped!
If for a particular one-to-one function f(2) = 13, what are the corresponding input and output
values for the inverse function?
Answers
Answer:
\(f^{-1}(13) = 2\).
Step-by-step explanation:
For function \(f\), the notation \(f(2) = 13\) means that when the input to the function is \(2\), the output would be \(13\).
The inverse function of a one-to-one function \(f\) is commonly denoted as \(\!f^{-1}\).
The inverse function undoes the action of the original function. In this question, \(f\) maps \(2\) to \(13\). Thus, \(f^{-1}\) would need to map \(13\!\) back to \(2\!\). Therefore, \(f^{-1}(13) = 2\) should be the corresponding input and output values.
What measure of central tendency can be used for any type of data?
А Mean
B Median
CMode
D All of the above.
Answers
Desperate Need Of Help

Answers
The domain and range of the graph above in interval notation include the following:
Domain = [-6, 3]
Range = [-3, 3]
What is a domain?In Mathematics and Geometry, a domain refers to the set of all real numbers (x-values) for which a particular function (equation) is defined.
In Mathematics and Geometry, the horizontal portion of any graph is used to represent all domain values and they are both read and written from smaller to larger numerical values, which simply means from the left of any graph to the right.
By critically observing the graph shown in the image attached above, we can reasonably and logically deduce the following domain and range:
Domain = [-6, 3] or -6 ≤ x < 3.
Range = [-3, 3] or -3 < y < 3
Read more on domain here: brainly.com/question/9765637
#SPJ1
3 1/2 miles in 1/2 hour
Answers
Answer:
? 7 miles an hour i guess
he data to the right represent the top speed (in kilometers per hour) of all the players (except goaltenders) in a certain soccer league. Construct (a) a relative frequency distribution (b) a frequency histogram, and (c) a relative frequency histogram. What percentage of players had a top speed between 14 and 17.9 km/h? What percentage of players had a top speed less than 13.9 km/h?
Answers
Answer:
a)
0.3212
b)
The percentage of player that had a top speed less than 13.9 km/h = 0.007259 x 100 = 0.7259%
Step-by-step explanation:
a) Construct relative frequency distribution?
Speed (km/hour) Number of players Relative frequency
10 – 13.9
14-17.9
18 – 21.9
22 – 25.9
26 – 29.9
30 – 33.9
4
8
18
76
268
177 4/551=0.007259
8/551=0.01451
18/551=0.03266
76/ 551=0.1379
268/551 = 0.486
177/551=0.3212
(b) frequency histogram:
Freq)
300 -
200 -
100-
0-
10 14 18 22 26 30 34
The percentage of player had top speed between 14 and 17.9 km/h was = 0.01451 x100 = 1.451%
The percentage of player that had a top speed less than 13.9 km/h = 0.007259 x 100 = 0.7259%


Mrs. Crosland asked students to factor the expression 282
8. The students offered the answers shown in the box.
Carlos:
Danny
Trener
2(14%
74x1)
407x - 2)
Which student(s) offered answer(s) equivalent to the original expression?
only Danny
only Irene
both Carlos and Danny
both Carlos and Irene
Answers
Well formatted version of the question can be found in the picture attached below :
Answer:
Both Carlos and Irene
Step-by-step explanation:
Given the expression (28x - 8)
Carlos : 2(14x - 4)
Danny : 7(4x - 1)
Irene : 4(7x - 2)
The factored expression Given by Carlos, Irene and Danny can be expanded to check if it gives the same expression as that Given in the question :
Carlos :
2(14x - 4)
2*14x - 2*4
28x - 8
Danny :
7(4x - 1)
7*4x - 7*1
28x - 7
Irene :
4(7x - 2)
4*7x - 4*2
28x - 8
From.the expanded solutions obtained ;
Both Carlos and Irene's solution corresponds to the factored form of the original equation and are Hence correct

An arborist is preparing the fuel mix for her chainsaw before climbing a tree to remove a dead limb. The two-stroke chainsaw
requires a 5% mix of engine oil to gas-that is, the amount of oil should be 5% of the amount of gas. How much engine oil should
be added to a jerry can that contains 3.8 gallons of gas?
(Type a whole number or a decimal)
Answers
Answer:
To determine the amount of engine oil needed, we need to find 5% of 3.8 gallons:
0.05 x 3.8 = 0.19
So, 0.19 gallons of engine oil should be added to the jerry can.
A jury pool consists of 31 people, 13 men and 18 women. Compute the probability that a randomly selected jury of 12 people is all male.
Answers
The first person you select has a probability of
\(\frac{13}{31}\)of being a male. The second time, there is a probability of:
\(\frac{12}{30}\text{.}\)Following the same reasoning, the probability of selecting 12 males is:
\(\frac{13}{31}\cdot\frac{12}{30}\cdot\frac{11}{29}\cdot\frac{10}{28}\cdot\frac{9}{27}\cdot\frac{8}{26}\cdot\frac{7}{25}\cdot\frac{6}{24}\cdot\frac{5}{23}\cdot\frac{4}{22}\cdot\frac{3}{21}\cdot\frac{2}{20}\text{.}\)Simplifying the above multiplication, we get:
\(\frac{13!}{31\cdot30\cdot29\cdot28\cdot27\cdot26\cdot25\cdot24\cdot23\cdot22\cdot21\cdot20}\approx9.2\times10^{-8}\text{.}\)Answer:
\(9.2\times10^{-8}=0.000000092.\)Divide Rs. 2379 into 3 parts so that their amounts after 2,3 and 4 years respectively may be equal, the rate of interest is 5% per annum at simple interest. The first part is..
Answers
Answer:
d Rs 828
Step-by-step explanation:
Let the three parts be x,y and z.
Then, x+
100
x×2×5
=y+
100
y×3×5
=z+
100
z×4×5
⇒x+
10
x
=y+
20
3y
=z+
5
z
10
11x
=
20
23y
=
5
6z
=k(say)
∴x=
11
10k
,y=
23
20k
,z=
6
5k
Given, x+y+z=2379
⇒
11
10k
+
23
20k
+
6
5k
=2379
⇒
1518
1380k+1320k+1265k
=2379
⇒3965k=2379×1518
⇒k=
3965
2379×1518
⇒ First part = Rs.
11×5
10×3×1518
= Rs. 828
Let the three parts be x,y and z.
Then, x+
100
x×2×5
=y+
100
y×3×5
=z+
100
z×4×5
⇒x+
10
x
=y+
20
3y
=z+
5
z
10
11x
=
20
23y
=
5
6z
=k(say)
∴x=
11
10k
,y=
23
20k
,z=
6
5k
Given, x+y+z=2379
⇒
11
10k
+
23
20k
+
6
5k
=2379
⇒
1518
1380k+1320k+1265k
=2379
⇒3965k=2379×1518
⇒k=
3965
2379×1518
⇒ First part = Rs.
11×5
10×3×1518
= Rs. 828
The average rate of growth for human hair is about 0.3 millimeters per day. How many days will it take a hair that is 12 millimeters long to grow to be 16.5 millimeters?
Answers
It will take 15 days for the hair to grow from 12mm to 16.5mm
What do you mean by average rate?By "average rate" in this context, we mean the typical or usual amount of hair growth per unit of time, which is often measured in millimeters per day. This rate can vary slightly depending on factors such as age, gender, genetics, diet, and overall health.
Let's first find out how much the hair needs to grow by subtracting its initial length (12mm) from its target length (16.5mm):
16.5mm - 12mm = 4.5mm
Now we can divide this growth by the average rate of hair growth to find the number of days it will take to grow this much:
4.5mm ÷ 0.3mm/day = 15 days
Therefore, it will take 15 days for the hair to grow from 12mm to 16.5mm.
To know more about average rate:
https://brainly.com/question/17219001
#SPJ1
An amount of $38,000 is borrowed for 10 years at 7.25% interest, compounded annually. If the loan is paid in full at the end of that period, how much must be paid back?
Use the calculator provided and round your answer to the nearest dollar.
Answers
Answer:
$76,516.77
Step-by-step explanation:
Use the compound interest formula. A = P(1 + r/n)^t. Subsitute the values in and solve.
Answer:
$76517Step-by-step explanation:
Given
Amount = $38000Interest rate = 7.25% Time = 10 yearsCompound = 1 per yearTotal:
38000*(1 + 0.0725)^10 = 76516.76 ≈ $76517 rounded to the nearest dollar