Solve the linear equation.
x/7 = -8
Answers
Answer:
x = - 56
Step-by-step explanation:
Given
\(\frac{x}{7}\) = - 8 ( multiply both sides by 7 to clear the fraction )
x = - 56
Answer:
x = -56
Step-by-step explanation:
i just simplified both sides of the equation you could say.
Related Questions
Please helppp I’m giving brainlyest

Answers
Answer:
B
Step-by-step explanation:
the shape will reflect b
Write an equation in point-slope form for the line that passes through the point with the given slope. point: (4,2) and m=3 *
Answers
Answer:
y - 2 = 3 (x - 4) - Point-Slope form.
y = 3x - 10 - Slope-intercept form.
Step-by-step explanation:
I will solve by using the formula:
y - y1 = m (x - x1)
Substitute:
y - 2 = 3 (x - 4)
This is the answer written in point-slope form.
I will put it into slope-intercept form.
Distribute:
y - 2 = 3x - 12
add 2 to both sides:
y = 3x - 10
Point (4 , 2) with a slope of 3 as an equation written in slope-intercept form looks like:
y = 3x - 10
The equation in point-slope form is y = 3x - 10 for the line that passes through the point at (4,2) with the given slope m=3.
What is the slope of the line?The slope of a line is defined as the angle of the line. It is denoted by m
Slope m = (y₂ - y₁)/(x₂ -x₁ )
Consider two points on a line—Point 1 and Point 2. Point 1 has coordinates (x₁,y₁) and Point 2 has coordinates (x₂, y₂)
Given that line that passes through the point at (4,2)
Let the equation in point-slope form would be
⇒ y - y₁ = m(x -x₁ )
Here, slope m = 3, x₁ = 4 and y₁ = 2
Substitute the values in the equation, and we get
⇒ y - 2 = 3 (x - 4)
⇒ y - 2 = 3x - 12
Add 2 to both sides of the equation
⇒ y = 3x - 10
Hence, the equation in point-slope form is y = 3x - 10 for the line that passes through the point at (4,2) with the given slope m = 3.
Learn more about Slope of Line here:
brainly.com/question/14511992
#SPJ2
what is 8x + 7 = 6x + 15.
Answers
Answer:
To solve for x in the equation 8x + 7 = 6x + 15, you need to isolate the variable (x) on one side of the equation.
First, you can start by subtracting 6x from both sides of the equation to get:
8x + 7 - 6x = 15
Simplifying this gives: 2x + 7 = 15
Next, you can subtract 7 from both sides of the equation to get: 2x = 8
Finally, divide both sides of the equation by 2 to solve for x: x = 4
Therefore, the solution for x in the equation 8x + 7 = 6x + 15 is x = 4
Answer:
x = 4
Step-by-step explanation:
To solve the equation 8x + 7 = 6x + 15, you can start by isolating the variable on one side of the equation. To do this, you can subtract 6x from both sides of the equation to get 2x + 7 = 15. Then, you can subtract 7 from both sides of the equation to get 2x = 8. Finally, you can divide both sides of the equation by 2 to get x = 4 1.
I hope that helps!
En un triangulo rectangulo se conoce la hipotenusa a = 5 m y un cateto b = 4 m. Calcula el cateto faltante y el angulo con respecto a la horizontal
Answers
The missing leg of right triangle is: 3 meters and the angle with respect to the horizontal is 53.13°
Here in a right triangle we know the hypotenuse a = 5 m and one leg b = 4 m.
Let us assume that 'c' be the horizontal leg of the right triangle.
Using Pythagoras theorem,
a² = b² + c²
Substituting values,
5² = 4² + c²
c² = 25 - 16
c² = 9
c = 3 m
Let us assume that θ be the angle with respect to the horizontal.
Consider the sine of the angle θ
sin(θ) = opposite side of angle θ / hypotenuse
sin(θ) = b/a
sin(θ) = 4/5
θ = 53.13°
Thus, the angle with respect to the horizontal = 53.13°
Learn more about the right triangle here:
https://brainly.com/question/6322314
#SPJ4
Given:
R is the midpoint of QS
Prove: PRQ = TRS

Answers
Answer:
Step-by-step explanation: Hello!
I don't remember all of the postulates to these, but I hope this will help you! Vertical angles are congruent, so both angles SRT and PRQ are congruent. This also means that line segments PQ and ST are congruent. You also know that angles Q and S are congruent which is given. By the ASA Theorem, when two angles and a side are congruent, then the triangles are congruent.
What is a reasonable domain for the data below?
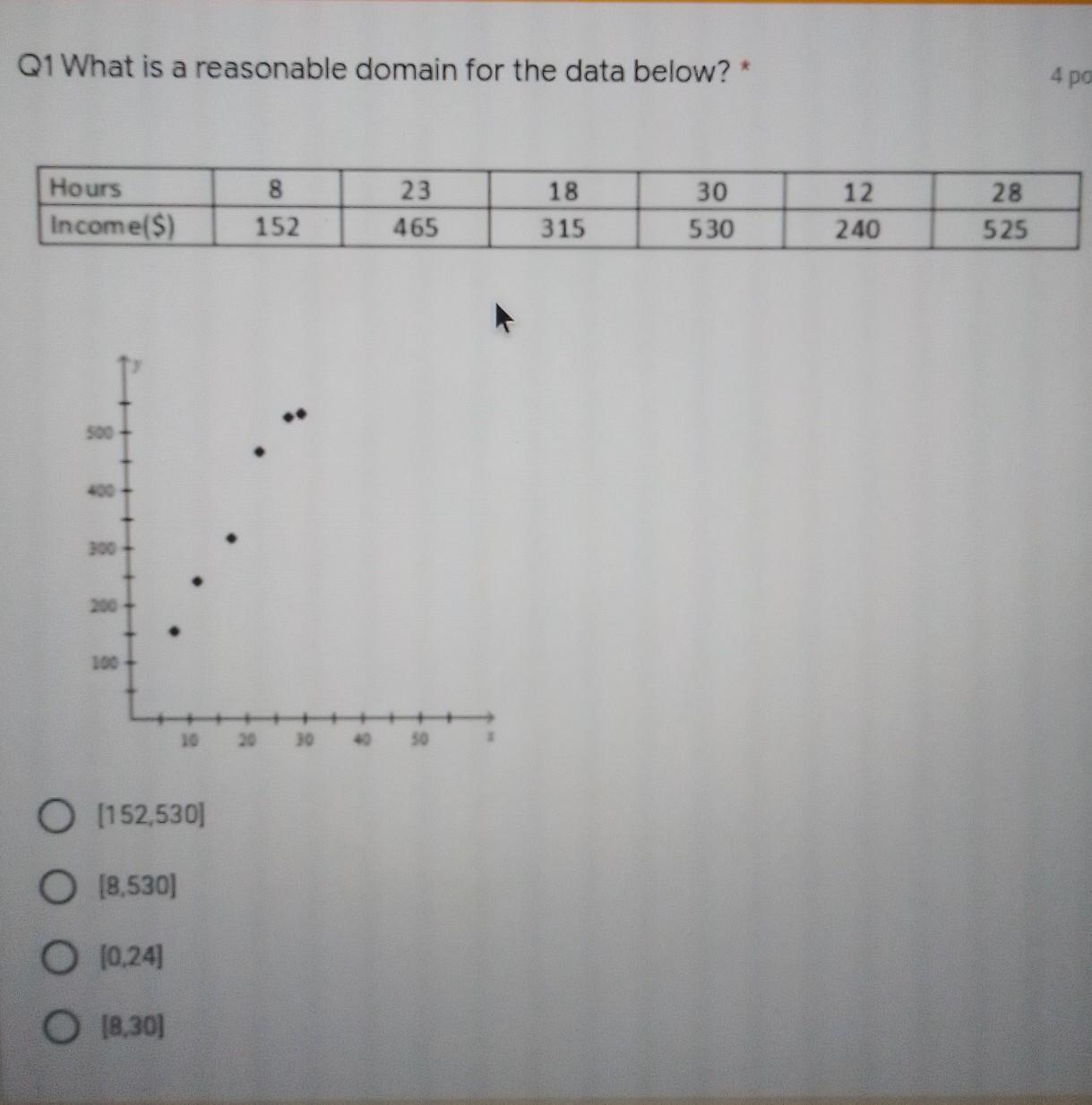
Answers
Answer:
[8,30]
Step-by-step explanation:
Domain means X. So you look for the smallest X value in your data and the largest X value in your data.
Find the slope
Help pls due in one hour

Answers
Graph the function using six values of its domain, y=30 + 5x
Answers
Answer: Here ya go bro, answer is in picture below


the maintenance supervisor of an assembly line has two tool cabinets, one at each end of the assembly line. each morning, she walks from one end of the line to the other, and she is equally likely to begin the walk at either end. in the two tool cabinets are a total of six flashlights. at the beginning of her walk, the supervisor takes a flashlight (if one is available) from the tool cabinet at that location, and at the end of her walk, she leaves a flashlight (if she possesses one) from the tool cabinet at that location. model the movement of flashlights using a discrete-time markov chain.
Answers
A Markov chain models flashlight movement in an assembly line with seven states and transition probabilities. Steady-state probabilities are calculated to determine long-run proportions in each state.
Let's denote the state of the system by the number of flashlights in the tool cabinet at the starting end of the assembly line. Since there are two tool cabinets and a total of six flashlights, the state space consists of seven possible states: 0, 1, 2, 3, 4, 5, or 6 flashlights in the tool cabinet at the starting end.
At each step of the Markov chain, the supervisor takes a flashlight from the tool cabinet at the starting end (if one is available), and leaves a flashlight (if she possesses one) in the tool cabinet at the ending end. This means that the Markov chain is time-homogeneous, since the transition probabilities depend only on the current state and not on the time at which the transition occurs.
Let's calculate the transition probabilities between the states. If the supervisor starts at a state with k flashlights in the tool cabinet at the starting end, then there are 6 - k flashlights in the tool cabinet at the ending end. Therefore, the probability of moving to a state with j flashlights in the tool cabinet at the starting end is equal to the probability of taking a flashlight from the starting end (which is k/6 if k > 0) multiplied by the probability of leaving a flashlight at the ending end (which is (6 - k)/6 if j > 0) multiplied by the probability of starting at the ending end (which is 1/2 since the supervisor is equally likely to start at either end). Formally, we have:
P(k, j) = (k/6) * ((6 - k)/6) * (1/2) if j > 0
P(k, 0) = (6 - k)/6 * (1/2) if j = 0
Note that since the supervisor always takes a flashlight from the tool cabinet at the starting end, it is impossible to transition to a state with more flashlights at the starting end than the current state (i.e., P(k, j) = 0 if j > k).
We can represent the transition probabilities between the states using a transition probability matrix, which is a 7x7 matrix where element (i,j) is the probability of transitioning from state i to state j:
| P(0,0) P(0,1) P(0,2) P(0,3) P(0,4) P(0,5) P(0,6) |
| P(1,0) P(1,1) P(1,2) P(1,3) P(1,4) P(1,5) P(1,6) |
| P(2,0) P(2,1) P(2,2) P(2,3) P(2,4) P(2,5) P(2,6) |
| P(3,0) P(3,1) P(3,2) P(3,3) P(3,4) P(3,5) P(3,6) |
| P(4,0) P(4,1) P(4,2) P(4,3) P(4,4) P(4,5) P(4,6) |
| P(5,0) P(5,1) P(5,2) P(5,3) P(5,4) P(5,5) P(5,6) |
| P(6,0) P(6,1) P(6,2) P(6,3) P(6,4) P(6,5) P(6,6) |
We can fill in the entries of this matrix using the transition probabilities we calculated above.
For example, to find P(2,3), we use the formula we derived above, with k=2 and j=3:
P(2,3) = (2/6) * ((6 - 2)/6) * (1/2) = 1/12
Similarly, we can find all the other entries of the matrix.
Once we have the transition probability matrix, we can use it to calculate the steady-state probabilities of each state. These are the probabilities that the system will be in each state in the long run, assuming that the Markov chain has reached a steady state. The can be found by solving the equation:
πP = π
where π is a row vector of the steady-state probabilities and P is the transition probability matrix. Since the sum of the probabilities in any row of P is 1, we also have the normalization condition that the sum of the probabilities in π is 1.
We can solve for π using various methods, such as row reduction or matrix inversion. The steady-state probabilities tell us the long-run proportion of time that the system will spend in each state.
In summary, we can model the movement of flashlights using a discrete-time Markov chain with a state space of seven possible states (corresponding to the number of flashlights in the tool cabinet at the starting end), and transition probabilities that depend on the probabilities of taking and leaving flashlights at each end of the assembly line. We can calculate the steady-state probabilities of each state, which tell us the long-run proportion of time that the system will spend in each state.
know more about Markov chain here: brainly.com/question/30998902
#SPJ11
Show that δ(x^2-a^2)=1/2a[δ(x-a)+ δ(x+a)]
δ(c0sθ- cosθ)= δ(θ-θ’)/sin θ’= δ (θ- θ’)/ sin θ
Answers
By using Dirac delta function, δ(c0sθ- cosθ)= δ(θ-θ’)/sin θ’= δ (θ- θ’)/ sin θ.
Here's how to show that δ(x^2-a^2)=1/2a[δ(x-a)+ δ(x+a)]
To show that δ(x^2-a^2)=1/2a[δ(x-a)+ δ(x+a)],
we can use the definition of Dirac delta function.
Dirac delta function is defined as follows:∫δ(x)dx=1and 0 if x≠0
In order to solve the given expression, we have to take the integral of both sides from negative infinity to infinity, which is given below:∫δ(x^2-a^2)dx=∫1/2a[δ(x-a)+ δ(x+a)]dx
To compute the left-hand side, we use a substitution u=x^2-a^2 du=2xdxWhen x=-a, u=a^2-a^2=0 and when x=a, u=a^2-a^2=0.
Therefore,-∞∫∞δ(x^2-a^2)dx=-∞∫∞δ(u)1/2adx=1/2a
Similarly, the right-hand side becomes:∫1/2a[δ(x-a)+ δ(x+a)]dx=1/2a∫δ(x-a)dx +1/2a∫δ(x+a)dx=1/2a + 1/2a=1/2a
Therefore,∫δ(x^2-a^2)dx=∫1/2a[δ(x-a)+ δ(x+a)]dxHence, δ(x^2-a^2)=1/2a[δ(x-a)+ δ(x+a)].
Next, we can show that δ(c0sθ- cosθ)= δ(θ-θ’)/sin θ’= δ (θ- θ’)/ sin θ as follows:We know that cosθ = cosθ' which implies θ=θ'+2nπ or θ=-θ'-2nπ.
Therefore, c0sθ-cosθ'=c0s(θ'-2nπ)-cosθ'=c0sθ'-cosθ' = sinθ'c0sθ-sinθ'cosθ'.
We can use the following identity to simplify the above expression:c0sA-B= c0sAcosB-sinAsinB
Therefore,c0sθ-cosθ' =sinθ'c0sθ-sinθ'cosθ'=sinθ'[c0sθ-sinθ'cosθ']/sinθ' =δ(θ-θ')/sinθ'
Hence,δ(c0sθ- cosθ)= δ(θ-θ’)/sin θ’= δ (θ- θ’)/ sin θ.
Learn more about Dirac delta function
brainly.com/question/32558176
#SPJ11
STATE AND PROVE THE FUNDAMENTAL THEOREM CALCULUS I (THE OWE ABOUT DIFFERENTIATING AN INTEGRAL)
Answers
The second fundamental theorem of calculus is a fundamental result in calculus because it allows us to use integration to solve problems that involve differentiation.
The fundamental theorem of calculus is divided into two parts, which are called the first and second fundamental theorem of calculus. The first fundamental theorem of calculus is a statement about the connection between differentiation and integration.
The theorem can be stated as follows:
Suppose that f(x) is a continuous function on the interval [a, b] and that F(x) is any antiderivative of f(x). Then the definite integral of f(x) from a to b is equal to
F(b) - F(a), or:
\(\int_{a}^{b}f(x)dx=F(b)-F(a)dx\)
The first fundamental theorem of calculus is a critical result in calculus because it allows us to evaluate definite integrals using antiderivatives. This means that we can use differentiation to solve problems that involve integration.The second fundamental theorem of calculus is a statement about how to differentiate integrals. The theorem can be stated as follows:
Suppose that f(x) is a continuous function on the interval [a, b], and that F(x) is an antiderivative of f(x). Then the derivative of the integral of f(x) from a to x is equal to f(x), or:
\(\frac{d}{dx}\int_{a}^{x}f(t)dt=f(x)dx\)
To know about calculus visit:
https://brainly.in/question/4630073
#SPJ11
Max recorded the math scores of five of his classmates in the table. Math Scores 98 76 100 88 82 What is the range of their test scores?
Answers
Answer:
24
Step-by-step explanation:
The range of a data set is the difference between the largest value and the smallest value.
{98 76 100 88 82}
The lowest grade is a 76 and the highest grade is a 100.
100-76=24
The range of the test scores should be 24.
The range of the given test scores should be; 24.
What is range of a data set?The range of a data set is the difference between the largest value and the smallest value.
We have been given a data set that represents the math scores of five of Max's classmates in the table. We are asked to determine the range of the given data set.
Math score: {98 76 100 88 82}
Since we know that the range is the difference between the largest and smallest values of the data set.
We can see that the lowest grade is a 76 and the highest grade is a 100.
Range = 100-76=24
Therefore, the range of the given test scores should be; 24.
Learn more about the domain and range of the function:
brainly.com/question/2264373
#SPJ6
what is the radius of a right circular cylinder with a volume of 12 in3 if it has a minimum surface area?
Answers
The value of radius of a right circular cylinder is 1,248 in for which the minimum surface area is obtained.
Define right circular cylinder?A cylinder with two circular bases and a line connecting their centers that is perpendicular to both bases.Volume of the right circular cylinder be;
v(c) = 12 in³ = π*r²*h
In which, h is the height of the cylinder,
Then , h = 12 / π*r²
Surface area of a right circular cylinder is:
S = area of base and top + lateral area
S(A) = 2*π*r² + 2*π*r*h ....eq 1
Put value of 'h' in equation (1)
S(r) = 2*π*r² + 2*π*r* ( 12 / π*r²)
S(r) = 2*π*r² + 24 /r
Differentiate both sides,
S´(r) = 4*π*r - 24 /r²
Put , S´(r) = 0 to get the critical points.
4*π*r - 24 /r² = 0
π*r - 6/r² = 0
π*r³ - 6 = 0
r³ = 1,91
r = 1,248 in
Check for the minimum surface area for r = 1,248 in.
Find the second derivative,
S´´(r) = 4*π + 48/r³
S´´(r) will always be positive.
Thus, the minimum surface area S is for r = 1,248 in.
To know more about the right circular cylinder, here
https://brainly.com/question/12762578
#SPJ4
Which graph represents the function p(x) = |x-1|?
Answers

Answer:
D
Step-by-step explanation:
The Smith family has 80 movies in their collection. The types of movies are shown in the table below. Smith Family Movies Type of Movie Percentage Drama 10% Action 25% Animated/Children’s 50% Comedy 15% How many of the movies in the collection are action movies? 8 12 20 40
Answers
Answer:
there are 20 movies
Step-by-step explanation:
Answer key for solve problems involving scale drawings
Answers
The key to solving problems involving scale drawings lies in understanding the concept of scale factor and using proportional relationships to find missing measurements or determine the actual size of objects.
When working with scale drawings, it is essential to comprehend the concept of scale factor. The scale factor represents the ratio of the measurements on the drawing to the corresponding measurements in the actual object. To solve problems involving scale drawings, start by identifying the given measurements and scale factor. Then, use proportional relationships to set up ratios between the measurements on the drawing and the actual object. By setting up these ratios, you can establish an equation and solve for the unknown measurement. For example, if the drawing shows a length of 5 centimeters with a scale factor of 2:1, you can set up the equation 5/2 = x/1, where x represents the actual length. Cross-multiplying and solving for x will give you the actual length. Additionally, you can use the scale factor to determine the actual size of objects. By multiplying the measurements on the drawing by the scale factor, you can find the corresponding measurements in the actual object. Remember to convert units if necessary and pay attention to any specific instructions or information given in the problem. By applying these techniques, you can effectively solve problems involving scale drawings.
Learn more about scale drawings here:
https://brainly.com/question/30771513
#SPJ11
Ignore the fact that this is answered, im not sure if the answer is right. What is the right answer?

Answers
Answer:
x = 5.5
Step-by-step explanation:
From rectangle KLMN, KM = 6x + 16, LN = 49
Find x
It can be seen that KM and LN are both equal diagonals in the rectangle.
Therefore,
KM = LN
6x + 16 = 49
6x = 49 - 16
6x = 33
Divide both sides by 6
x = 33/6
x = 5.5
Maya is making a miniature dinner table for her little sister. She wants the table top to be similar to their real dinner table top. Find the width of the miniature table top to the nearest tenth of a centimeter.

Answers
Answer:
4.9cm
Step-by-step explanation:

Carson is a songwriter who collects royalties on his songs whenever they are played in a commercial or a movie. Carson will earn $20 every time one of his songs is played in a commercial and he will earn $120 every time one of his songs is played in a movie. Carson's songs were played on 5 more commercials than movies, and his total earnings on the royalties from all commercials and movies was $380. Determine the number of commercials and the number of movies on which Carson's songs were played.
Answers
Answer:
\(M=\frac{280}{140} =2\)
\(C=2+5=7\)
(2 Movies and 7 Commercials)
Step-by-step explanation:
Let's represent every time Carson's songs are played in a commercial as C and in movies as M.
Set up the following equations:
\(20C+120M=380\) (1)
\(C=M+5\) (2)
Substitute equation 2 for equation 1:
\(20(M+5)+120M=380\)
Distribute:
\(20M+100+120M=380\)
Simplify:
\(140M=280\)
Divide both sides by 140:
\(M=\frac{280}{140} =2\)
Substitute 2 as M back into either original equation, I will use (2):
\(C=2+5=7\)
Answer:
Step-by-step explanation:
help is it a b c or d

Answers
Answer:
The last one)
6 21/64 in.3
Step-by-step explanation:
Simply multiply LxWxH, (length x width x height.)
LxWxH= 3 1/2in x 1 7/8 in x 2 3/4 in= 6 21/64 in.3.
A sweet seller has 48 Kaju burfies and 72 badam becafio. He
wants to stack them in such a way
that each stack has the
same
number and they take
the least area of the train, What
is the numbers of burfies in each stack.
Answers
In the given problem, we can stack the sweets in six stacks, each with 24 sweets. So, there will be 24 Kaju burfies in each stack.
How to Solve the Problem?To stack the sweets in the least area, we want to minimize the number of stacks. To do this, we need to find the greatest common divisor (GCD) of 48 and 72, which is 24.
Therefore, we need to stack the sweets in groups of 24.
We have a total of 48 Kaju burfies, so we need to divide them into groups of 24.
48 / 24 = 2
So, we can stack the Kaju burfies in two stacks of 24 each.
We also have 72 badam becafio, which we need to stack in groups of 24.
72 / 24 = 3
So, we can stack the badam becafio in three stacks of 24 each.
Thus, we can stack the sweets in six stacks, each with 24 sweets.
So, there will be 24 Kaju burfies in each stack.
Learn more about greatest common divisor here: https://brainly.com/question/29399179
#SPJ1
In the given problem, we can stack the sweets in six stacks, each with 24 sweets. So, there will be 24 Kaju burfies in each stack.
How to Solve the Problem?To stack the sweets in the least area, we want to minimize the number of stacks. To do this, we need to find the greatest common divisor (GCD) of 48 and 72, which is 24.
Therefore, we need to stack the sweets in groups of 24.
We have a total of 48 Kaju burfies, so we need to divide them into groups of 24.
48 / 24 = 2
So, we can stack the Kaju burfies in two stacks of 24 each.
We also have 72 badam becafio, which we need to stack in groups of 24.
72 / 24 = 3
So, we can stack the badam becafio in three stacks of 24 each.
Thus, we can stack the sweets in six stacks, each with 24 sweets.
So, there will be 24 Kaju burfies in each stack.
Learn more about greatest common divisor here: https://brainly.com/question/29399179
#SPJ1
Skyler punches Johnny eighteen times. Johnny kicks Skyler fifteen times. Which one is more painful?
Answers
Answer
Jhonny's kick is more painful
Step-by-step explanation:
because kicks are more painful than punches.
An adult elephant that is 8 ft tall casts a shadow that is 4 ft long. Find the height of a
statue that casts a 9 ft shadow.
Answers
Answer: Hope this helps!
18 ft
Step-by-step explanation: Good luck :)
This question sounds confusing but if you just look at the numbers it is much easier.
Elephant height: 8 ft
Elephant shadow: 4ft
Statue height: ?
Statue shadow: 9ft
As you can see the elephant's height is double the size of the shadow, if you put those as ratios the statues height will also be double its shadow, from there just double 9ft and you will get your answer. 9x2=18ft
{20, 30, 40, 50, 60, 70, 80}
The range of this set of numbers is
A)
0
B)
20
50
D)
60
Answers
It is C 50 Hopefully this is right
Answer:
60 or D
Step-by-step explanation:
The Range is the difference between the lowest and highest values.
80-20= 60
in the united states, according to a 2018 review of national center for health statistics information, the average age of a mother when her first child is born in the u.s. is 26 years old. a curious student at cbc has a hypothesis that among mothers at community colleges, their average age when their first child was born is lower than the national average. to test her hypothesis, she plans to collect a random sample of cbc students who are mothers and use their average age at first childbirth to determine if the cbc average is less than the national average. use the dropdown menus to setup this study as a formal hypothesis test. [ select ] 26 [ select ] 26
Answers
To set up this study as a formal hypothesis test, the null hypothesis (H0) would be that the average age of first childbirth among mothers at community colleges (CBC) is equal to the national average of 26 years old.
The alternative hypothesis (Ha) would be that the average age of first childbirth among CBC mothers is lower than the national average.
The next step would be to collect a random sample of CBC students who are mothers and determine their average age at first childbirth. This sample would be used to calculate the sample mean.
Once the sample mean is obtained, it can be compared to the national average of 26 years old. If the sample mean is significantly lower than 26, it would provide evidence to reject the null hypothesis in favor of the alternative hypothesis, supporting the student's hypothesis that the average age of first childbirth among CBC mothers is lower than the national average.
The student plans to conduct a hypothesis test to determine if the average age of first childbirth among mothers at CBC is lower than the national average.
To know more about alternative hypothesis visit :
brainly.com/question/33149605
#SPJ11
What is the equation of the graph of
the line that passes through the
coordinates (4,9) and (6, 15)?
A. y = -3x - 3
B. y = -3x + 3
C. y = 3x - 3
D. y = 3x + 3
Answers
In summary the answer is (C) y = 3x - 3.
To find the equation of the line passing through the coordinates (4,9) and (6, 15), we can use the slope-intercept form of the equation of a line, which is: y = mx + b, where m is the slope of the line and b is the y-intercept.
To find the slope of the line passing through the given coordinates, we can use the formula: m = (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are the two points on the line.
Substituting the given values, we get: m = (15 - 9) / (6 - 4) = 6 / 2 = 3
So the slope of the line is 3.
To find the y-intercept, we can use one of the given points and the slope. Let's use the point (4, 9): y = mx + b, 9 = 3(4) + b, b = 9 - 12, b = -3
So the y-intercept is -3.
Therefore, the equation of the line passing through the coordinates (4, 9) and (6, 15) is: y = 3x - 3
Hence, the answer is (C) y = 3x - 3.
To know more about Equation related question visit:
https://brainly.com/question/29657983
#SPJ11
Solve the fallowing system of equations using the graphing method
Y=2x-4
Y=-1/2x+1
Answers
The lines intersect at the point (3, 2). Therefore, the solution to the system of equations y = 2x - 4 and y = (-1/2)x + 1 is x = 3 and y = 2.
To solve the system of equations y = 2x - 4 and y = (-1/2)x + 1 using the graphing method, we can graph both equations on the same coordinate plane and find the point of intersection.
To graph y = 2x - 4, we can start by plotting the y-intercept, which is -4. From there, we can use the slope of 2 to plot additional points. For example, if we move one unit to the right along the x-axis, we would move two units up along the y-axis to get the point (1, -2). Similarly, if we move one unit to the left, we would move two units down to get the point (-1, -6). By connecting these points, we can graph the line y = 2x - 4.
To graph y = (-1/2)x + 1, we can start by plotting the y-intercept, which is 1. From there, we can use the slope of (-1/2) to plot additional points. For example, if we move two units to the right along the x-axis, we would move one unit down along the y-axis to get the point (2, 1/2). Similarly, if we move two units to the left, we would move one unit up to get the point (-2, 3/2). By connecting these points, we can graph the line y = (-1/2)x + 1.
The point where the two lines intersect is the solution to the system of equations. By looking at the graph, we can see that the lines intersect at the point (3, 2). Therefore, the solution to the system of equations y = 2x - 4 and y = (-1/2)x + 1 is x = 3 and y = 2.
Learn more about system of equations here
https://brainly.com/question/13729904
#SPJ11
you may not use the break and continue statements within the same set of nested loops. t/f
Answers
The given statement is false because In programming, the break and continue statements serve different purposes and can be used independently or together within nested loops.
The break statement is used to exit the current loop prematurely. When encountered, it terminates the loop and continues with the next statement after the loop. This can be useful when a specific condition is met, and you want to stop the execution of the loop immediately.
The continue statement, on the other hand, is used to skip the current iteration of a loop and move on to the next iteration. It allows you to skip certain iterations based on a specific condition without terminating the entire loop.
Both break and continue statements can be used within nested loops. In such cases, the break statement will exit only the innermost loop it is placed in, while the continue statement will skip to the next iteration of the innermost loop.
By using break and continue strategically within nested loops, you can control the flow of execution based on specific conditions. This flexibility allows you to fine-tune the behavior of your program and optimize its efficiency.
For more such questions on programming visit:
https://brainly.com/question/23275071
#SPJ11
Note : This is a computer science question
Bank ABC offers a 10 -year CD that pays a 5.0% interest compounded annually.
Bank XYZ also offers a 10 -year CD that pays 4.95% interest compounded daily.
How much would a $1,000 initial investment in each bank's CD be worth at maturity?
Bank ABC: ______
Bank XYZ: ______
(Enter answer in the form: $x,x×x.xx )
Answers
A $1,000 initial investment in Bank ABC's CD would be worth $1,628.89 at maturity. A $1,000 initial investment in Bank XYZ's CD would be worth $1,622.82 at maturity.
The formula to calculate the value of a CD after a specific duration at a specific interest rate compounded annually is given by:
A = P(1 + r/n)^(nt)
where P is the principal,
r is the annual interest rate,
n is the number of times compounded per year,
t is the number of years, and
A is the value of the CD at maturity.
Here, we need to calculate the value of a $1,000 initial investment in each bank's CD at maturity.
Let's calculate the value of a $1,000 investment in Bank ABC's CD.
P = $1,000
r = 5.0% compounded annually
t = 10 years
n = 1
We have all the values; let's put them in the formula and solve:
A = $1,000(1 + 0.05/1)^(1x10)A = $1,628.89
Therefore, a $1,000 initial investment in Bank ABC's CD would be worth $1,628.89 at maturity.
Let's calculate the value of a $1,000 investment in Bank XYZ's CD.
P = $1,000
r = 4.95% compounded daily
t = 10 years
n = 365
We have all the values; let's put them in the formula and solve:
A = $1,000(1 + 0.0495/365)^(365x10)A = $1,622.82
Therefore, a $1,000 initial investment in Bank XYZ's CD would be worth $1,622.82 at maturity.
To know more about investments, visit:
https://brainly.com/question/31411302
#SPJ11
What is the value of x that makes the statement true?
7x + 9 = 5x + 39
x =
Answers
Answer:
15
Step-by-step explanation:
7x+9=5x+39
7x-5x=39-9
2x=30
30/2=x
x=15
7x -5 = 39-9
2x =20
30\2 x=15