The volume of a cone is 75 and the radius is 5 . What is the height
Answers
Answer:
Step-by-step explanation:
h≈2.86
Answer:
Volume:75 Radius:5
Step-by-step explanation:
Related Questions
Find the measurements of X
pt 3

Answers
Answer:
180 p
Step-by-step explanation:your welcome
A parabola has a maximum value of 4 at x= -1, a y-intercept of 3, and an x-intercept of 1.
Which graph matches the description? PLZ HURRY

Answers
Answer:
The answer is C
Step-by-step explanation:
Plz mark as Brainliest
A parabola has a maximum value of 4 at x= -1, a y-intercept of 3, and an x-intercept of 1. The x-intercepts are -3 and 1. So, The second graph is the right one.
We have given that,
A parabola has a maximum value of 4 at x = -1,
A y-intercept of 3, and an x-intercept of 1.
What is the maximum point of the graph?The maximum value of a graph refers to the point on the graph where the y-coordinate has the largest value.
A maximum graph is one that represents the largest value of the y-coordinate on the graph.
So, The second graph is the right one.
Note that when x = 1, y (the maximum) is 4,
and that, The x-intercepts are -3 and 1.
To learn more about the maximum value click here:
brainly.com/question/1286349
#SPJ5
Consider the scatter plot, its line of best fit, and the corresponding residual plot of each data set. State whether a linear model is appropriate for the data and justify your answer.
Linear regression equation: y = 3.93x - 11.33, r = 0.8241

Answers
Considering the graphs given here between the scatter plot, its line of best fit and residual plot; linear regression equation is more appropriate for the data because it help to determine a regression correlation in two variables.
What is the linear regression equation?
In statistics, a regression equation is used to determine whether there is any link between two sets of data. A variable's value can be predicted using linear regression analysis based on the value of another variable.
The Linear Regression equation can be understandable by following justification:
Y= mX +b
Given, Y = { 2,4,6,8,10,12}
X = {9, 2,1,12,25,48}
∵ y = 3.93x - 11.33
∵ r = 0.8241
∴ Value of Y = 3
∴ Value of X = {0.8241 + 11.33r} ÷ {0.93}
Thus for the scatter plot dots more understandable with linear equation and for residual plot dots depicts non-linear equation. The two variables X and Y.
To know more about linear regression equation refer:
https://brainly.com/question/25311696
#SPJ1
begin{tabular}{|r|l|r|r|} \hline 3 & Below are your numerical inputs for the problem: \\ \hline 4 & Initial Cost (\$) & 390000 \\ \hline 5 & Year 1 Revenues (\$) & 192000 \\ \hline 6 & Year 1 Costs (\$) & 125000 \\ \hline 7 & Inflation & 2.75% \\ \hline 8 & Project Duration (years) & 6 \\ \hline 9 & Depreciation Method & \\ \hline 10 & Tax Rate & \\ \hline 11 & Net Working Capital (\% oft+1 Revenues) & MACRS \\ \hline 12 & Salvage Value (\$) & 28.00% \\ \hline 13 & Cost of Capital & 15.00% & 245000 \\ \hline \end{tabular} How much are the year 1 operating cash flows (OCF)? How much is the depreciation expense in year 3 ? What is the change in Net Working Capital (NWC) in year 2? What is the net cash flow from salvage (aka, the after-tax salvage value, or ATSV)? What is the project's NPV? Would you recommend purchasing the ranch? Briefly explain.
Answers
Information is needed to evaluate the project's financial viability, considering factors such as the initial investment, expected cash flows, cost of capital, and project duration.
To calculate the year 1 operating cash flows (OCF), we need to subtract the year 1 costs from the year 1 revenues:
OCF = Year 1 Revenues - Year 1 Costs
OCF = $192,000 - $125,000
OCF = $67,000
To find the depreciation expense in year 3, we need to determine the depreciation method. The provided information is incomplete regarding the depreciation method, so we cannot calculate the depreciation expense in year 3 without knowing the specific method.
The change in Net Working Capital (NWC) in year 2 can be determined by multiplying the Net Working Capital percentage (given as a percentage of t+1 revenues) by the year 1 revenues and subtracting the result from the year 2 revenues:
Change in NWC = (Year 2 Revenues - Net Working Capital percentage * Year 1 Revenues) - Year 1 Revenues
Without the specific Net Working Capital percentage or Year 2 Revenues values, we cannot calculate the exact change in NWC in year 2.
The net cash flow from salvage (ATSV) is calculated by multiplying the Salvage Value percentage by the Initial Cost:
ATSV = Salvage Value percentage * Initial Cost
ATSV = 28% * $390,000
ATSV = $109,200
To calculate the project's NPV, we need the cash flows for each year, the cost of capital, and the project duration. Unfortunately, the information provided does not include the cash flows for each year, so we cannot calculate the project's NPV.
To know more about investment visit:
https://brainly.com/question/29547577
#SPJ11
The complete question is:
Below are your numerical inputs for the problem: 4 & Initial Cost (\$) & 390000 5 & Year 1 Revenues (\$) & 192000 6 & Year 1 Costs (\$) & 125000 7 & Inflation & 2.75% 8 & Project Duration (years) & 6 9 & Depreciation Method & 10 & Tax Rate & 11 & Net Working Capital (\% oft+1 Revenues) & MACRS 12 & Salvage Value (\$) & 28.00% 13 & Cost of Capital & 15.00% & 245000 How much are the year 1 operating cash flows (OCF)? How much is the depreciation expense in year 3 ? What is the change in Net Working Capital (NWC) in year 2? What is the net cash flow from salvage (aka, the after-tax salvage value, or ATSV)? What is the project's NPV? Would you recommend purchasing the ranch? Briefly explain.
2. find the perimeter of a rectangle with a length
of q and a width of (q-2).
Answers
Answer: 4q-4
Step-by-step explanation:
2(q+q-2) = 2(2q-2) = 4q-4
A cone and a cylinder have the same radius and height. The volume of the cone is 100π (pi) cubic feet. What is the volume of the cylinder?
Answers
Answer:
The volume of the cylinder is \(300\pi\) cubic feet.
Step-by-step explanation:
From Geometry we remember that volumes of a cone and a cylinder with the same radius (\(R\)), measured in feet, and height (\(h\)), measured in feet, are defined by the following equations:
Cone
\(V_{co} = \frac{1}{3}\pi\cdot R^{2}\cdot h\) (1)
Cylinder
\(V_{cy} = \pi\cdot R^{2}\cdot h\) (2)
The ratio of the volume of the cylinder to the volume of the cone is:
\(\frac{V_{cy}}{V_{co}} = 3\) (3)
If we know that \(V_{co} = 100\pi\,ft^{3}\), then the volume of the cylinder is:
\(V_{cy} = 3\cdot V_{co}\)
\(V_{cy} = 300\pi\,ft^{3}\)
The volume of the cylinder is \(300\pi\) cubic feet.
por favor lo necesito

Answers
Answer:
i dont know spanish soryy.
Step-by-step explanation:
What percent of 120 is 72
A- 86.4%
B- 60%
C- 1.67%
D- 0.6%
Answers

question 9 of 10 explain how you can determine the sign of the sum of two integers if one integer is positive and the other integer is negative.
Answers
To determine the sign of the sum of two integers when one integer is positive and the other is negative, we can follow a simple rule based on their magnitudes.
If the magnitude of the positive integer is greater than the magnitude of the negative integer, the sum will be positive. This is because the positive integer outweighs the negative integer, resulting in a positive value.
On the other hand, if the magnitude of the negative integer is greater than the magnitude of the positive integer, the sum will be negative. In this case, the negative integer dominates and determines the sign of the sum.
In both scenarios, the sign of the larger magnitude integer takes precedence and determines the sign of the sum. It is important to note that the sum will always have the sign of the integer with the larger magnitude, regardless of the specific values of the integers involved.
By considering the magnitudes of the integers, we can easily determine the sign of their sum when one integer is positive and the other is negative.
Know more about Magnitudes here:
https://brainly.com/question/31022175
#SPJ11
hey mate iam indian
claim 10 points

Answers
Answer:
k
Step-by-step explanation:
Simplify \(\frac{sec(a)-csc(a)}{sec(a)+csc(a)}\)
Answers
The simplified version of (sec a - cosec a) / (sec a + cosec a) is cosec 2a(cosec 2a - 2) / (sec²a - cosec²a).
What is trigonometry?The study of correlations between triangles' side lengths and angles is known as trigonometry. The field was created in the Hellenistic era in the third century BC as a result of the use of geometry in astronomical research.
Given:
(sec a - cosec a) / (sec a + cosec a)
Multiply the numerator and denominator by (sec a - cosec a)
(sec a - cosec a) / (sec a + cosec a) × (sec a - cosec a)
(sec²a + cosec²a -2sec a cosec a) / (sec²a - cosec²a)
As we know,
\(sec^2a + cosec^2a = sec^2a \ cosec^2a\)
sec² a cosec² a - 2sec a cosec a / (sec²a - cosec²a)
sec a cosec a (sec a cosec a - 2) / (sec²a - cosec²a)
cosec 2a(cosec 2a - 2) / (sec²a - cosec²a)
To know more about trigonometry:
https://brainly.com/question/14272510
#SPJ1
please help on number 8!! it would be much appreciated

Answers
Answer:
a.) 135 degrees
b.) 45 degrees
c.) 45 degrees
Step-by-step explanation:
Use this link to see a visual representation on how to solve for these types of angles, it lets you click on any type of angle and see how it corresponds to other angles within the parallel line and traversal, give it a try!
https://www.mathsisfun.com/geometry/alternate-exterior-angles.html
The officers of a high school senior class are planning to rent buses and vans for a class trip. Each bus can transport 72 students, requires 3 chaperones, and costs $1,400 to rent. Each van can transport 9 students, requires chaperone, and costs $100 to rent. Since there are 720 students in the senior class that may be eligible to go on the trip, the officers must plan to accommodate at least 720 students. Since only 45 parents have volunteered to serve as chaperones, the officers must plan to use at most 45 chaperones. How many vehicles of each type should the officers rent in order to minimize the transportation costs? What are the minimal transportation costs?
Answers
So the minimal transportation cost is $8,700, and it can be achieved by renting 6 buses and 27 vans.
Let's start by defining our variables. Let b be the number of buses and v be the number of vans to be rented. We want to minimize the transportation costs, so our objective function is:
C = 1400b + 100v
We also have two constraints:
The total number of students that can be transported cannot be less than 720:
72b + 9v ≥ 720
The total number of chaperones cannot be more than 45:
3b + v ≤ 45
Now we can solve for b and v. Let's solve the second constraint for v:
v ≤ 45 - 3b
Substituting this inequality into the first constraint, we get:
72b + 9(45 - 3b) ≥ 720
Simplifying and solving for b, we get:
b ≥ 6
So we know that we need to rent at least 6 buses. Since we cannot rent a fraction of a bus or van, b must be an integer. Let's try b = 6 and see if it satisfies the second constraint:
3(6) + v ≤ 45
v ≤ 27
Since v must also be an integer, the largest integer that satisfies this inequality is v = 27. Now we can calculate the total cost:
C = 1400(6) + 100(27) = 8700
To know more about equation,
https://brainly.com/question/28243079
#SPJ11
Hannah needs to calculate the cotangent of an angle. She uses the ratio
opposite leg
for her calculation. Did Hannah correctly calculate the cotangent of the angle?
adjacent leg
A
B.
Yes, Hannah correctly calculated the cotangent of the angle.
adjacent leg
No, Hannah should have used the ratio
opposite leg
hypotenuse
No, Hannah should have used the ratio
opposite leg
O c.
D.
No, Hannah should have used the ratio
adjacent leg
hypotenuse

Answers
Answer:
B. No, Hannah should have used the ratio \( \frac{adjacent}{opposite} \)
Step-by-step explanation:
✍️The formula for calculating cotangent of an angle is given as:
\( cot = \frac{adjacent}{opposite} \).
The ratio, \( \frac{opposite}{adjacent} \), used by Hannah is the formula for calculating tangent of an angle.
Therefore, Hannah did not calculate the cotangent of the angle correctly.
She should have used, the ratio, \( \frac{adjacent}{opposite} \) instead.
Which expression is equivalent to (4 7i)(3 4i)? â€""16 37i 12 â€"" 28i 16 â€"" 37i 37 16i.
Answers
Equivalent expressions are expressions that have the same value
The equivalent expression of \((4 +7i)(3 +4i)\) is \(-16+37i\)
The expression is given as:
\((4 +7i)(3 +4i)\)
Expand the equation
\((4 +7i)(3 +4i) = 4(3 +4i) +7i(3 +4i)\)
Distribute the equation, as follows:
\((4 +7i)(3 +4i) = 12 +16i +21i +28i^2\)
In complex numbers,
\(i^2 = -1\)
So, we have:
\((4 +7i)(3 +4i) = 12 +16i +21i +28(-1)\)
Evaluate the product
\((4 +7i)(3 +4i) = 12 +16i +21i -28\)
Combine like terms
\((4 +7i)(3 +4i) = 12-28+16i +21i\)
Evaluate like terms
\((4 +7i)(3 +4i) = -16+37i\)
Hence, the equivalent expression of \((4 +7i)(3 +4i)\) is \(-16+37i\)
Read more about equivalent expressions at:
https://brainly.com/question/2972832
Which of the following is a trinomial with a constant term?
A. x + 2y + 10
a
B. X
c. Y6+ 8y3 + 64y
+
D. x2 + y
Answers
Answer:
The answer would be
A. x + 2y + 10
A constant term is considered any term that does not change or have a variable with it. 10 is the only displayed constant term.
Answer:
\(\\ \sf\longmapsto x^2+y\)
Step-by-step explanation:
Trinomial means the expression has 3 roots.
In the last one
x has degree 2 so it has 2roots. And there is another variable namely y so another root.Total 3 roots
At an ice cream shop, Roy orders 3 scoops of ice cream and 1 topping for $3.95. Pete orders 2 scoops and 2 toppings for $3.10. What is the cost per scoop and per topping?a. $0.35 per scoop and $1.20 per topping/ b. $1.20 per scoop and $0.35 per topping/ c. $3.10 per scoop and $0.85 per topping/ d. $2.25 per scoop and $0.85 per topping
Answers
The price for 1 scoop of ice cream and the price for 1 topping is $1.20 and $0.35 respectively.
Suppose the price for 1 scoop of ice cream = x
The price for 1 topping = y
What is a linear equation?An equation of the form ax+by+c=0 is called a linear equation where a, b and c are real numbers.
According to the question
3x+y=3.95.......(1)
2x+2y=3.10.......(2)
Multiply equation (1) by 2 on both sides
6x+2y=7.90.....(3)
Subtracting the equation (2) from equation(3)
4x=4.80
x=1.20
So, y = 0.35
So, the price for 1 scoop of ice cream =$1.20
The price for 1 topping = $0.35
Hence, the price for 1 scoop of ice cream and price for 1 topping is $1.20 and $0.35 respectively.
To get more about linear equations visit:
https://brainly.com/question/14323743
Answer:
B
Step-by-step explanation:
Jadon wants to know how much water it takes to fill the water tower. The water tower is made up of a cone, cylinder, and a half-sphere. For this question, use 3. 14 for , and round a non-integer answer to the hundredths place. The total volume of the water tower is
cubic meters
Answers
Answer:
Step-by-step explanation:
3444
in what one year period of the study did the rabbit populations see the greatest decrease?
Answers
Answer- The rabbit population decreased in 2013 and 2015 in some areas of up to 80%
In circle C, QP and QR are tangent segments and m
What is the m

Answers
The value or measure of ∠PQR in the given circle where PQ & RQ are tangents from same external point Q is 52°, found by applying theorem in circle C and considering quadrilateral CPQR.
What are tangents?The word "tangent" refers or means "to touch". The Latin word for the same is "tangere". The line that intersects the circle exactly at one point on its circumference or boundary of circle and never enters the circle's interior is a tangent. A circle can have many or infinite tangents. They are always perpendicular to the radius. A tangent of a circle is straight line that touches or intersects externally the circle at only one point without entering the interior of circle.
Consider the circle C, Given that
∠PCR=128°
QP & RQ are tangents from same point Q, which means
QP= QR {tangents from same external point are equal in length}
CP & CR are radius from the centre C & also perpendicular to the tangents, which means:
CP ⟂ QP
CR ⟂ QR
∠CPQ=90°
∠CRQ=90°
Consider the Quadrilateral CPQR,
∠C + ∠P + ∠Q + ∠R = 360° {angle sum property of quadrilateral}
128 + 90 + ∠Q + 90 = 360
128 + 180 +∠Q = 360°
∠Q = 360° - 180 - 128
∠Q = 360° - 308
∠Q = 52°
Therefore the measure of ∠PQR is 52°.
To know more about tangents, visit:
https://brainly.com/question/23265136
#SPJ1
A train leaves train station A and heads due west for 105 miles to reach train station B. Another train leaves train station A at the same time and travels 85 miles to train station C in a direction 45 north of west from station A. To the nearest mile, how far is train station C from train station B
Answers
The distance between train station C and train station B is 75.02095678 miles, using the law of cosines.
In the question, we are given that a train leaves train station A and heads due west for 105 miles to reach train station B. Another train leaves train station A at the same time and travels 85 miles to train station C in a direction 45 north of west from station A.
We are asked to calculate the distance between train station C and train station B.
The given scenario can be shown by the attached diagram in the form of a triangle, where A depicts train station A, B depicts train station B, and C depicts train station C, with the angle between them being 45°.
The distance between train station A and train station B can be shown as AB = c = 105 miles.
The distance between train station A and train station C can be shown as AC = b = 85 miles.
The distance between train station B and train station C can be shown as BC = a = x miles.
By the law of cosines, in the triangle ABC, we can say that:
a² = b² + c² - 2bc cos A,
or, x² = 85² + 105² - 2(85)(105) cos 45°),
or, x² = 7225 + 11025 - 17850(0.707106781),
or, x² = 18250 - 12621.85604,
or, x² = 5628.143956,
or, x = √5628.143956 = 75.02095678.
Thus, the distance between train station C and train station B is 75.02095678 miles, using the law of cosines.
Learn more about the law of cosines at
https://brainly.com/question/1491613
#SPJ4

What is 10/30 simpflited
Answers
Answer:
1/3
Step-by-step explanation:
Answer:
1/3
Step-by-step explanation:
A road sign is in the shape of a square. What is the measure of each angle on the sign? Round to the nearest tenth.
Answers
Each angle on a square road sign measures 90 degrees.
A square is a quadrilateral with four equal sides and four right angles. In a square, all angles are congruent, meaning they have the same measure. Since a square has four angles, each angle is equal to the total sum of the interior angles of a square divided by four.
The total sum of the interior angles of a square can be calculated using the formula (n - 2) * 180 degrees, where n is the number of sides. For a square, n = 4, so the total sum of the interior angles is (4 - 2) * 180 = 2 * 180 = 360 degrees.
To find the measure of each angle, we divide the total sum of the interior angles by the number of angles, which is 4 in the case of a square:
360 degrees / 4 angles = 90 degrees.
Therefore, each angle on a square road sign measures 90 degrees.
Learn more about square here
https://brainly.com/question/14198272
#SPJ11
23° is equal to
23
O1
23
Answers
Answer:
Hi, there!
23
Step-by-step explanation:
The value of (23) is equal to twenty three.
23
I hope it's helps you
Step by step explanation
when is gradient -40 for bode plot
Answers
Without knowing the transfer function and the arrangement of poles and zeros, it is not possible to determine the frequency at which the gradient is -40 dB/decade in a Bode plot.
In a Bode plot, the gradient represents the slope of the line that connects two consecutive asymptotes. Each asymptote corresponds to a pole or zero in the transfer function.
Therefore, to determine when the gradient is equal to -40, we need to find the frequency at which two consecutive asymptotes have a 40 dB difference in magnitude.
In general, the magnitude of the transfer function for a system with a single pole or zero can be expressed as:
|H(jω)| = K / |1 + jω/ωp| (for a pole)
or
|H(jω)| = K |1 + jω/ωz| (for a zero)
where K is the system gain, ωp is the pole frequency, and ωz is the zero frequency.
When there are multiple poles and zeros, the magnitude is the product of the individual magnitudes. The phase angle also depends on the number and type of poles and zeros.
For a single pole, the magnitude asymptote has a slope of -20 dB/decade (i.e., a decrease of 20 dB for each increase in frequency by a factor of 10). Therefore, two consecutive poles will have a 40 dB difference in magnitude when the frequency is such that the first pole's magnitude asymptote intersects the second pole's magnitude asymptote. This occurs when the frequency is one decade below the second pole's frequency.
For a single zero, the magnitude asymptote has a slope of +20 dB/decade (i.e., an increase of 20 dB for each increase in frequency by a factor of 10).
Therefore, two consecutive zeros will have a 40 dB difference in magnitude when the frequency is such that the first zero's magnitude asymptote intersects the second zero's magnitude asymptote. This occurs when the frequency is one decade above the second zero's frequency.
In general, when there are multiple poles and zeros, the frequency at which two consecutive asymptotes have a 40 dB difference in magnitude will depend on the specific values and arrangement of the poles and zeros.
Your question seems incomplete. I could not find the exact question details online so I answered in general.
Click the below link, to learn more about bode plot:
https://brainly.com/question/29799447
#SPJ11
Select all of the shapes below which are enlargements of shape X.

Answers
The shape A is the enlargement of shape C.
Dilation is the process of increasing the size of an item without affecting its form. Depending on the scale factor, the object's size can be raised or lowered. There is no effect of dilation on the angle.
An enlargement of a shape is a transformation that results in a larger or smaller version of the original shape while keeping the shape's angles the same. The process involves multiplying the length, width, and height of the original shape by a common scale factor.
From the graph, the shape A is the enlargement of shape C.
More about the dilation link is given below.
https://brainly.com/question/2856466
#SPJ1
Please help me solve this question, I don’t get it at all

Answers
Answer:
32 units
Step-by-step explanation:
∠LON = 2(∠LMN) = 2(60°) = 120°
120°/360° = 1/3
length of minor arc LN = (1/3)(96) = 32 units
Someone help please
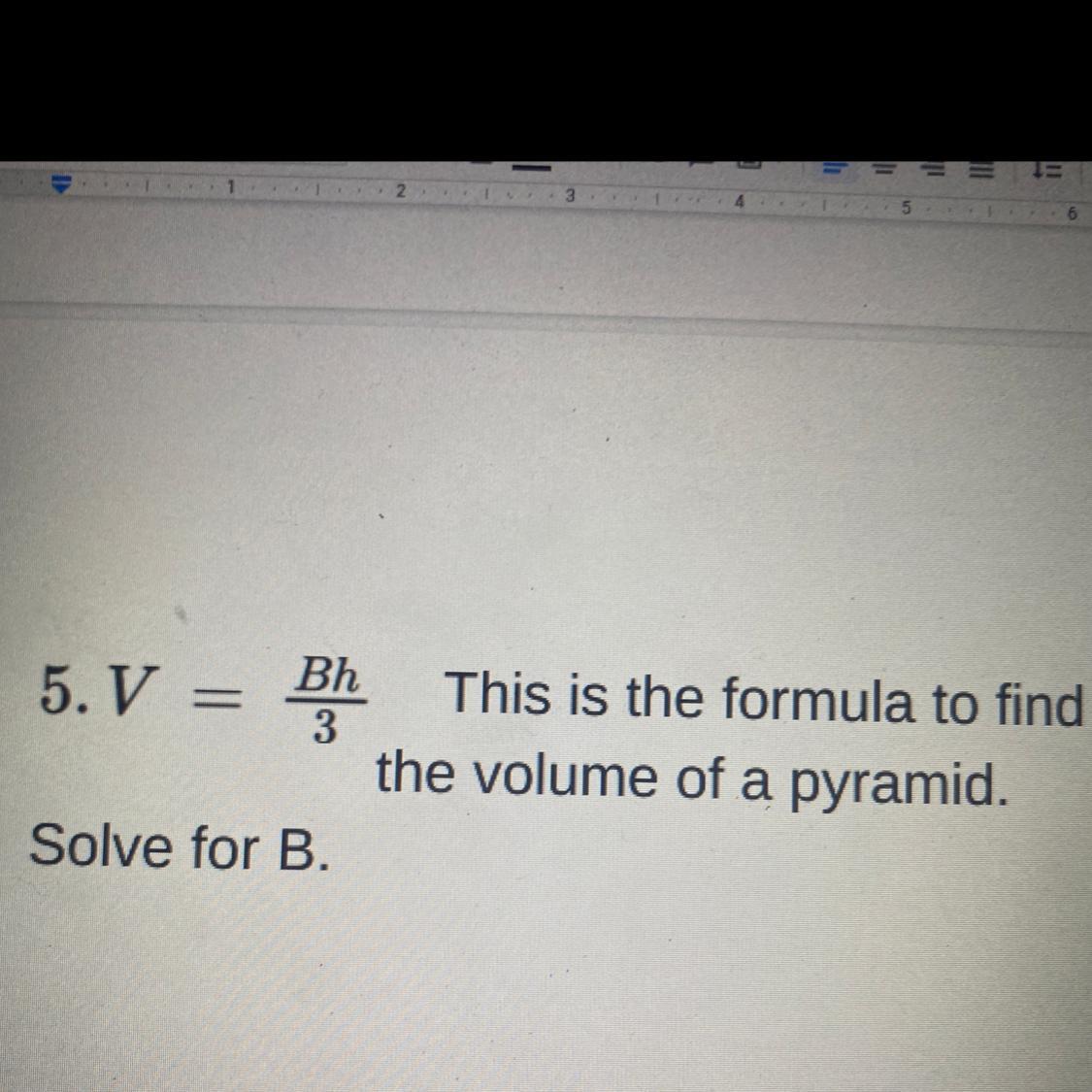
Answers
Answer:
\(b = \frac{3v}{h} \)
Answer:
Step-by-step explanation:
First you multiple both sides by 3
3v=Bh
Than divide by h
You get
3v/h=B
PLEASE HELP ME SOLVE THESE, I WOULD LIKE DETAILED ANSWERS THAT EXPLAIN EVERY STEP. MUCH APPRECIATED
1.The line y=x+1 intersects the graph of y = x² - 3x - 11 at the points A and B .
Find the co-ordinates of A and B. You must show all your working .
2. A is the point (5,-5) and B is at the point (9,3).
a)Find the co-ordinates of the midpoint.
b) Find the length of AB
3.A is at the point (5,7) and B is at the point(9,-1)
a)Find the length of AB
b)Find the equation of the line AB
4.Find the gradient of the line that is perpendicular to the line 3y=4x-5
5. A is the point (1,5) and B is the point (3,9).M is the midpoint of AB
i)Find the co-ordinates of M
ii)Find the equation of the line that is perpendicular to AB and passes through M.
Give your answer in the form : y=mx+c
Answers
1. The he intersection points A and B are:
A(-2, -1) and B(6, 7)
2. Midpoint is (7, -1)
3. length of AB is 4√5
How to solve for the linesTo find the intersection points A and B, set y = x + 1 and y = x² - 3x - 11 equal to each other:
x + 1 = x² - 3x - 11
Now, rearrange the equation to set it equal to zero:
x² - 4x - 12 = 0
Factor the quadratic equation:
(x - 6)(x + 2) = 0
Solve for x:
x = 6, x = -2
Now plug the x-values back into the equation of either line (y = x + 1) to find the corresponding y-values:
For x = 6: y = 6 + 1 = 7
For x = -2: y = -2 + 1 = -1
So the intersection points A and B are:
A(-2, -1) and B(6, 7)
a) To find the midpoint of A(5,-5) and B(9,3), use the midpoint formula:
Midpoint = ((x1 + x2)/2, (y1 + y2)/2)
Midpoint = ((5 + 9)/2, (-5 + 3)/2) = (14/2, -2/2) = (7, -1)
b) To find the length of AB, use the distance formula:
Distance = √((x2 - x1)² + (y2 - y1)²)
Distance = √((9 - 5)² + (3 - (-5))²) = √(4² + 8²) = √(16 + 64) = √80
Length of AB = 4√5 (simplified
a) To find the length of AB, use the distance formula:
Distance = √((x2 - x1)² + (y2 - y1)²)
Distance = √((9 - 5)² + (-1 - 7)²) = √(4² + (-8)²) = √(16 + 64) = √80
Length of AB = 4√5 (simplified)
b) To find the equation of the line AB, first find the slope:
m = (y2 - y1)/(x2 - x1) = (-1 - 7)/(9 - 5) = (-8)/4 = -2
Next, use the point-slope form with one of the points (A or B), say A(5,7):
y - y1 = m(x - x1)
y - 7 = -2(x - 5)
Now, convert the equation to the slope-intercept form (y = mx + c):
y = -2x + 10 + 7
y = -2x + 17
To find the gradient of the line that is perpendicular to 3y = 4x - 5, first find the gradient of the given line:
3y = 4x - 5 => y = (4/3)x - 5/3
The gradient of the given line is 4/3. To find the gradient of the perpendicular line, find the negative reciprocal:
m_perpendicular = -1/(4/3) = -3/4
i) To find the midpoint M of A(1,5) and B(3,9), use the midpoint formula:
Midpoint = ((x1 + x2)/2, (y1 + y2)/
Read more on gradient of a line here:https://brainly.com/question/16949303
#SPJ1
Evaluate the expression x
x(2 – 5y)²
when x= = -5 and y=-3.
Answers
\(\displaystyle -5(2-5(-3))^2=-5(17)^2=-1445\)