Use this scenario to answer questions 3-4: Peter was a waiter that was paid at a rate of $8 per hour plus tips. He earned a total of $200 including $54 in tips.
Given the scenario above, write an equation to represent the scenario. Let h = the number of hours
Free brainliest included! :)
Answers
Related Questions
Find the interest Earned
$1200 at 7% for 5 years
Show ur work please and thanks
Answers
Answer:
84
Step-by-step explanation:
So,
1% of 1200 = 12
12x7 = 84
Hello may I please get some help with this question

Answers
6x^2=-3x+1 to the nearest hundredth
Answers
The solutions to the quadratic equation 6x² = -3x + 1 to the nearest hundredth are -0.73 and 0.23.
What are the solutions to the quadratic equation?Given the quadratic equation in the question:
6x² = -3x + 1
To solve the quadratic equation 6x² = -3x + 1, we can rearrange it into standard form, where one side is set to zero:
6x² + 3x - 1 = 0
Now we can solve the equation using the quadratic formula, which states that for an equation in the form ax² + bx + c = 0, the solutions for x are given by:
\(x = \frac{-b \±\sqrt{b^2-4ac} }{2a}\)
Here; a = 6, b = 3, and c = -1.
Let's substitute these values into the quadratic formula:
\(x = \frac{-b \±\sqrt{b^2-4ac} }{2a}\\\\ x= \frac{-3 \±\sqrt{3^2-4\ *\ 6\ *\ -1} }{2*6}\\\\x = \frac{-3 \±\sqrt{9+24} }{12}\\\\x = \frac{-3 \±\sqrt{33} }{12}\\\\x = -0.73, \ x=0.23\)
Therefore, the values of x are -0.73 and 0.23.
Learn more about quadratic equations here: brainly.com/question/1863222
#SPJ1
Carolyn leases a new Hyundai Elantra by paying $2600 up front and $170 a month over three years. The lease also stipulates he will be charged $0.12 per mile for every mile over 36,000. If she puts 40,693 miles on the car, what will be the total cost of the lease?
Answers
4,693 x $0.12= $563.16 (cost of the mile overage)
3 years= 36 months. (Multiply 3 x 12)
Now multiply 36 x $170 a month = $6,120.
$2,600 (up front cost) + $563.16 (cost of mile overage) + $6,120 (cost over 3 years) = $9.283.16 ( answer)
5.5.3 Suppose X and Y have a bivariate normal distribution with , , , , and . Determine the following. Round your answers to three decimal places (e.g. 98.765). (a) Enter your answer in accordance to the item a) of the question statement (b) Enter your answer in accordance to the item b) of the question statement (c) Enter your answer in accordance to the item c) of the question statement
Answers
The question is incomplete. The complete question is :
Suppose X and Y have a bivariate normal distribution with \($\sigma_X = 0.04, \sigma_Y = 0.08, \mu_X = 3.00, \mu_Y = 7.70$\) and ρ = 0.
Determine the following. Round your answers to three decimal places (e.g. 98.765).
(a). \($P(2.90 < X < 3.10) =$\)
(b). \($P(7.60 < X < 7.80) =$\)
(c). P(2.90 < X < 3.10, 9.60 < Y < 7.80) =
Solution :
We have
\($X \sim N (\mu_X=3, \sigma_X^2=0.04^2)$\) and
\($Y \sim N (\mu_Y=7.7, \sigma_Y^2=0.08^2)$\)
a). The required probability is
\($P(2.90 < X < 3.10) =$\) \($P\left(\frac{2.9-3}{0.04}< Z < \frac{3.1-3}{0.04}\right)$\)
= P(-2.5 < Z < 2.5) = P(Z < 2.5) - P(Z < -2.5)
= P(Z < 2.5) - [1-P(Z < 2.5)]
= 2P(Z < 2.5) - 1
= 2(0.99379) - 1
= 0.98758
≈ 0.988
b). The required probability is
\($P(7.6 < X < 7.8) =$\) \($P\left(\frac{7.6-7.7}{0.08}< Z < \frac{7.8-7.7}{0.08}\right)$\)
= P(-1.25 < Z < 1.25) = P(Z < 1.25) - P(Z < -1.25)
= P(Z < 1.25) - [1-P(Z < 1.25)]
= 2P(Z < 1.25) - 1
= 2(0.89435) - 1
= 0.7887
≈ 0.789
c). Since, ρ = 0, so the X and Y are independent. Thus the required probability is :
P(2.90 < X < 3.10, 9.60 < Y < 7.80) = P(2.9 < X < 3.1) x P(7.6 < Y < 7.8)
= (0.98758)(0.7887)
= 0.77890
≈ 0.779
If the work required to stretch a spring 3 ft beyond its natural length is 6 ft-lb, how much work is needed to stretch it 9 in. beyond its natural length?
Answers
Answer:
3/8
Step-by-step explanation:
Given that:
Work required to stretch a string:
3 ft = 6ft - lb
The work required to stretch it 9 inches
Given that :
Work(W) = kx
Take the integral of W at 3 fts beyond its natural length;
W = ∫kx dx at 0 to 3
W = k ∫xdx at 0 to 3
W = 6
W = k[x²/2] at x =0 to x = 3
6 = k[3² /2] - 0
6 = k[9/2]
12 = 9k
k = 12/9 = 4/3 = 1.333
Converting inches to feet:
1 inch 0.0833 ft
9 inches = 0.75 ft
W = ∫kx dx at 0.75 to 0
W = 4/3 ∫xdx at 0 to 0.75 = 3/4
W = 4/3[x²/2] at x =0.75 to 0
W = 4/3[(3/4)²/2] at 0.75 to 0
W = 4/3[(9/16) / 2]
W = 4/3 * (9/16 * 1/2)
W = 36/96
W = 6/16 = 3/8 ft - lbs
a
29
Solve each percent equation. Remember "of" means multiply and "is" means equal.
At your school, 74% of students bought their lunch at the cafeteria. There are
1250 students in the school. How many students bought their lunch?
925
students who brought their lunch. YUM!!
Answers
Answer
925 students brought their lunch.
Explanation
First let's rewrite the equation.
You know that "of" means multiply and "is" means equal.
Okay, so let's break it down.
The question says, "At your school, 74% of students brought their lunch at the cafeteria. There are 1250 students in the school."
This means that 74% of 1250 students brought their lunch at the cafeteria.
You are trying to find how many students brought their lunch. This will be x.
So the equation would be this.
74% × 1250 = x
74% is 0.74.
0.74 × 1250 = x
0.74 × 1250 = 925
So 925 students brought their lunch.
In trapezoid ABCD, line AC is a diagonal and angle ABC is congruent to angle ACD. Find AC if the lengths of the bases line BC and line AD are 12m and 27m, respectively
Answers
Since ΔABC and ΔACD are similar triangles, therefore the length of AC is 18 m.
What are Similar Triangles?Similar triangles are triangles with corresponding sides that have the same ratio.
Thus:
AD is parallel to BC (bases of a trapezoid are parallel)
Therefore:
∠ACB = ∠CAD (alternate interior angles)
This implies that, ΔABC ~ ΔACD by AA similarity theorem.
Thus:
AC/DA = CB/AC
Substitute
AC² = 12 × 27
AC = √324
AC = 18 m
Therefore, since ΔABC and ΔACD are similar triangles, therefore the length of AC is 18 m.
Learn more about similar triangles on:
brainly.com/question/11899908
#SPJ1
You loan your brother $300 and charge him 2% simple annual interest. He promises to
repay you one year later. How much willyour brother have to pay you?
in 1 year
Also plz show the steps
Answers
Answer:
$306
Step-by-step explanation:
In one year, the 2% annual interest would have been applied once. Therefore, your brother would pay you 1.02 * 300 which is 306.
Hope this helps :)
Answer: 306 dollars
===========================================
Work Shown:
i = P*r*t ..... simple interest formula
i = 300*0.02*1
i = 6
Your brother pays $6 in simple interest on top of the $300 in principal loaned to him. The total amount he pays back is 300+6 = 306 dollars.
----------
Another way to calculate the answer is to do these steps
A = P*(1+r*t)
A = 300*(1+0.02*1)
A = 300*(1.02)
A = 306
The 1.02 represents a 2% increase when going from 300 to 306.
PLEASE I NEED HELP IN THIS
HERE IS THE PICTURE IS JUST ONE QUESTION

Answers
Answer:
f(x) = -5/9x - 11/9
Step-by-step explanation:
Consider f(x) = y
so if x = -4 => y = 1 and x = 5 => y = -4
so (-4,1) and (5,-4) should be on the same linear equation
Slope m = (y2 - y1)/(x2 - x1)
m = (-4 - 1)/(5 - -4) = (-5)/(9) = -5/9
y = mx + b
given m = -5/9, x = -4, y = 1
1 = -5/9(-4) + b
b = 1 - 20/9
b = 9/9 - 20/9 = -11/9
so y = -5/9x - 11/9
or f(x) = -5/9x - 11/9
I need help on these anybody?

Answers
The complete labels to the parts of the circle such as tangent, diameter, radius and secant are found in the attchment.
What are the parts of a circle?The various parts of a circle are:
Center: The point inside the circle that is equidistant from all points on the circumference.
Circumference: The distance around the circle.
Radius: A line segment from the center of the circle to any point on the circumference.
Diameter: A line segment that passes through the center of the circle and has its endpoints on the circumference.
Chord: A line segment with both endpoints on the circumference.
Tangent: A line that intersects the circle at only one point, called the point of tangency.
Secant: A line that intersects the circle at two points.
Learn more about parts of a circle at: https://brainly.com/question/13093152
#SPJ1

Factor the expression using the GCF.
7 + 14 =
Answers
Answer:
1+2
Step-by-step explanation:
The table shows how a 3-square-foot shelf is split into 6 sections for storing art materials. How many square feet are there for storing paint?
Answers
The number of square feet that are there for storing paint is 1/2
How to determine the number of square feet are there for storing paint?From the question, we have the following parameters that can be used in our computation:
Area of the table = 3-square-foot
Number of sections = 6 sections
The number of square feet is there for storing paint is calculated as
The number of square feet = Area of the table/Number of sections
Substitute the known values in the above equation, so, we have the following representation
The number of square feet = 3-square-foot/6
Evaluate the quotient
The number of square feet = 1-square-foot/2
This gives
The number of square feet = 1/2 -square-foot
Hence, the square feet is 1/2
Read more about areas at
https://brainly.com/question/25292087
#SPJ1
Complete question
The table shows how a 3-square-foot shelf is split into 6 sections for storing art materials. How many square feet are there for storing paint?
Area (square feet) Sections
3 6
6 12
9 18
The measure of one small angles of a right triangle is 45 less than twice the measure of the other small angle. Find the measure of both angles
Answers
Answer:
x + x - 45 = 90
2x - 45 = 90
2x = 135
x = 67.5, so x - 45 = 22.5
The other two angles measure 22.5° and 67.5°.
Which function is graphed below?

Answers
Answer:
Piecewise function;
y = 2x - 2 where x < 2
4 where 2 ≤ x ≤ 5
y = x + 1 where x > 5
Step-by-step explanation:
Function graphed represents the piecewise function.
1). Equation of the line with y-intercept (-2) and slope 'm'.
Since, slope of the line = \(\frac{\text{Rise}}{\text{Run}}\)
= \(\frac{2}{1}\)
= 2
Therefore, equation of this segment will be in the form of y = mx + b,
⇒ y = 2x - 2 where x < 2
2). Equation of a horizontal line,
y = 4 where 2 ≤ x ≤ 5
3). Equation of the third line in the interval x > 5
Let the equation of the line is,
y = mx + b
Where m = slope of the line
b = y-intercept
Here, slope 'm' = \(\frac{\text{Rise}}{\text{Run}}\)
= \(\frac{2}{2}\)
= 1
Equation of this line will be,
y = 1(x) + b
y = x + b
Since, this line passes through (5, 6),
6 = 5 + b
b = 6 - 5 = 1
Therefore, equation of this line will be,
y = x + 1 where x > 5
Graphed piecewise function is,
y = 2x - 2 where x < 2
4 where 2 ≤ x ≤ 5
y = x + 1 where x > 5
Which is an odd monomial function?
O y = 2x²
y = 5x9
O y=3
Answers
Answer:
1) y=2x²
hope it helps;)
Answer:
y=2x^3
Step-by-step explanation:
On edge 2021
Which linear function has the same y-intercept as the one that is represented by the graph?
On a coordinate plane, a line goes through points (3, 4) and (5, 0).
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 3, negative 1, 1, 3. Column 2 is labeled y with entries negative 4, 2, 8, 14.
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 4, negative 2, 2, 4. Column 2 is labeled y with entries negative 26, negative 18, negative 2, 6.
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 5, negative 3, 3, 5. Column 2 is labeled y with entries negative 15, negative 11, 1, 5.
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 6, negative 4, 4, 6. Column 2 is lab
eled y with entries negative 26, negative 14, 34, 46.
Answers
The linear function that has the same y-intercept as the given graph is the equation y = -2x + 10, corresponding to option 3.
To determine the linear function with the same y-intercept as the graph, we need to find the equation of the line passing through the points (3, 4) and (5, 0).
First, let's find the slope of the line using the formula:
slope (m) = (change in y) / (change in x)
m = (0 - 4) / (5 - 3)
m = -4 / 2
m = -2
Now that we have the slope, we can use the point-slope form of a linear equation to find the equation of the line:
y - y1 = m(x - x1)
Using the point (3, 4) as our reference point, we have:
y - 4 = -2(x - 3)
Expanding the equation:
y - 4 = -2x + 6
Simplifying:
y = -2x + 10
Now, let's check the given options to find the linear function with the same y-intercept:
Option 1: The table with x-values (-3, -1, 1, 3) and y-values (-4, 2, 8, 14)
The y-intercept is not the same as the given line. So, this option is not correct.
Option 2: The table with x-values (-4, -2, 2, 4) and y-values (-26, -18, -2, 6)
The y-intercept is not the same as the given line. So, this option is not correct.
Option 3: The table with x-values (-5, -3, 3, 5) and y-values (-15, -11, 1, 5)
The y-intercept is the same as the given line (10). So, this option is correct.
Option 4: The table with x-values (-6, -4, 4, 6) and y-values (-26, -14, 34, 46)
The y-intercept is not the same as the given line. So, this option is not correct.
Therefore, the linear function that has the same y-intercept as the given graph is the equation y = -2x + 10, corresponding to option 3.
for such more question on linear function
https://brainly.com/question/9753782
#SPJ8
Let Q be an orthogonal matrix with an eigenvalue λ1=1. Let x be an eighenvector beloinging to λ1. Show that x is also an eigenvector of QT
Answers
If Q is an orthogonal matrix with an eigenvalue λ1 = 1, then x, the eigenvector corresponding to λ1, is also an eigenvector of QT with an eigenvalue λ2 = λ1 * (QT * x).
To show that x is also an eigenvector of QT, we need to demonstrate that QT * x is a scalar multiple of x.
Given that Q is an orthogonal matrix, we know that QT * Q = I, where I is the identity matrix. This implies that Q * QT = I as well.
Let's denote x as the eigenvector corresponding to the eigenvalue λ1 This means that Q * x = λ1 * x.
Now, let's consider QT * x. We can multiply both sides of the equation Q * x = λ1 * x by QT:
QT * (Q * x) = QT * (λ1 * x)
Applying the associative property of matrix multiplication, we have:
(QT * Q) * x = λ1 * (QT * x)
Using the fact that Q * QT = I, we can simplify further:
I * x = λ1 * (QT * x)
Since I * x equals x, we have:
x = λ1 * (QT * x)
Now, notice that λ1 * (QT * x) is a scalar multiple of x, where the scalar is λ1. Therefore, we can rewrite the equation as:
x = λ2 * x
where λ2 = λ1 * (QT * x).
This shows that x is indeed an eigenvector of QT, with the eigenvalue λ2 = λ1 * (QT * x).
In conclusion, if Q is an orthogonal matrix with an eigenvalue λ1 = 1, then x, the eigenvector corresponding to λ1, is also an eigenvector of QT with an eigenvalue λ2 = λ1 * (QT * x).
for more such question on matrix visit
https://brainly.com/question/2456804
#SPJ8
Solve the following for θ, in radians, where 0≤θ<2π.
−7cos2(θ)+4cos(θ)+6=0
Select all that apply:
1.07
3.96
0.31
2.32
1.68
2.43
Answers
Answer:correct answers are 3.96
2.32
Step-by-step explanation:We can solve this quadratic equation in cos(θ) by using the substitution u = cos(θ):
-7u^2 + 4u + 6 = 0
Now we can use the quadratic formula to solve for u:
u = (-b ± sqrt(b^2 - 4ac)) / 2a
where a = -7, b = 4, and c = 6. Substituting these values, we get:
u = (-4 ± sqrt(4^2 - 4(-7)(6))) / 2(-7)
u = (-4 ± sqrt(136)) / (-14)
u = (2 ± sqrt(34)) / 7
Therefore, either:
cos(θ) = (2 + sqrt(34)) / 7
or:
cos(θ) = (2 - sqrt(34)) / 7
Since 0 ≤ θ < 2π, we can find the two solutions in the interval [0, 2π) by using the inverse cosine function:
θ = arccos((2 + sqrt(34)) / 7)
θ = arccos((2 - sqrt(34)) / 7)
Using a calculator, we find:
21x² - 2x + 1/2 =0
find the following quadratic equation by factorization method
PLESE SOMEONE HELP
Answers
Step-by-step explanation:
21x²-2x +1/2 = 0
x² - 2x ×21 + 1/2× 21 = 0
Select the choice that translates the following verbal phrase correctly to algebra: (2 points)
the difference of m and 7 increased by 15
a.) m − (7 + 15)
b.) 7m + 15
c.) (m − 7) + 15
d.) m − 7 ÷ 15
Answers
3 6 9 12 15 18 21 24 27 30 is odd or even numbers?
Answers
Answer: Half of them are even and half of them are odd.
Step-by-step explanation:
The even numbers are 6, 12, 18, 24, and 30. An even number is defined as a number that is divisible by 2, meaning it has no remainder when divided by 2. For example, 6 divided by 2 equals 3 with no remainder, so 6 is even.
The odd numbers are 3, 9, 15, 21, and 27. An odd number is defined as a number that is not divisible by 2, meaning it has a remainder of 1 when divided by 2. For example, 9 divided by 2 equals 4 with a remainder of 1, so 9 is odd.
Therefore, out of the given numbers, half of them are even and half of them are odd.
________________________________________________________
Find the area of the triangle below.
Be sure to include the correct unit in your answer.

Answers
Answer:
28 yd²
Step-by-step explanation:
finding the area of a triangle is (base * height) / 2.
(14*4)=56
56/2=28
Write the polynomial as the product of linear factors and list all the zeros of the function:
f(x) = x^4 - 16
Answers
\(a^2-b^2=(a-b)(a+b)\)
Therefore
\(f(x)=x^4-16\\f(x)=(x^2-4)(x^2+4)\\f(x)=(x-2)(x+2)(x^2+4)\)
\((x-2)(x+2)(x^2+4)=0\\x=2 \vee x=-2\)
6x^2 + 9x = 0 :) please help !!
Answers
Solution for 6x^2+9x=0 equation:
Simplifying
6x2 + 9x = 0
Reorder the terms:
9x + 6x2 = 0
Solving
9x + 6x2 = 0
Solving for variable 'x'.
Factor out the Greatest Common Factor (GCF), '3x'.
3x(3 + 2x) = 0
Ignore the factor 3.
Subproblem 1
Set the factor 'x' equal to zero and attempt to solve:
Simplifying
x = 0
Solving
x = 0
Move all terms containing x to the left, all other terms to the right.
Simplifying
x = 0
Subproblem 2
Set the factor '(3 + 2x)' equal to zero and attempt to solve:
Simplifying
3 + 2x = 0
Solving
3 + 2x = 0
Move all terms containing x to the left, all other terms to the right.
Add '-3' to each side of the equation.
3 + -3 + 2x = 0 + -3
Combine like terms: 3 + -3 = 0
0 + 2x = 0 + -3
2x = 0 + -3
Combine like terms: 0 + -3 = -3
2x = -3
Divide each side by '2'.
x = -1.5
Simplifying
x = -1.5
Solution
x = {0, -1.5}
Divide both sides by a constant to simplify:
3X (2x + 3) = 0
———————— = X ( 2x/3 + 1) = 0
3
Isolate the x to one side:
X = -3/2 and x = 0
NO LINKS!! URGENT HELP PLEASE!!
1. Find the area of a regular octagon. Each side is 12 m.
2. The perimeter of a regular polygon is 72 feet. An exterior angle of the polygon measures 40°. Find the length of each side.
3. If the perimeter of a regular pentagon is 50 in. Find the area. Show a drawing and work please.
Answers
Answer:
1) 695.3 m²
2) 8 ft
3) 172.0 in²
Step-by-step explanation:
Question 1To find the area of a regular polygon, we can use the following formula:
\(\boxed{\begin{minipage}{5.5cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{s^2n}{4 \tan\left(\dfrac{180^{\circ}}{n}\right)}$\\\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\end{minipage}}\)
Given the polygon is an octagon, n = 8.
Given each side measures 12 m, s = 12.
Substitute the values of n and s into the formula for area and solve for A:
\(\implies A=\dfrac{(12)^2 \cdot 8}{4 \tan\left(\dfrac{180^{\circ}}{8}\right)}\)
\(\implies A=\dfrac{144 \cdot 8}{4 \tan\left(22.5^{\circ}\right)}\)
\(\implies A=\dfrac{1152}{4 \tan\left(22.5^{\circ}\right)}\)
\(\implies A=\dfrac{288}{\tan\left(22.5^{\circ}\right)}\)
\(\implies A=695.29350...\)
Therefore, the area of a regular octagon with side length 12 m is 695.3 m² rounded to the nearest tenth.
\(\hrulefill\)
Question 2The sum of an interior angle of a regular polygon and its corresponding exterior angle is always 180°.
If the exterior angle of a polygon measures 40°, then its interior angle measures 140°.
To determine the number of sides of the regular polygon given its interior angle, we can use this formula, where n is the number of sides:
\(\boxed{\textsf{Interior angle of a regular polygon} = \dfrac{180^{\circ}(n-2)}{n}}\)
Therefore:
\(\implies 140^{\circ}=\dfrac{180^{\circ}(n-2)}{n}\)
\(\implies 140^{\circ}n=180^{\circ}n - 360^{\circ}\)
\(\implies 40^{\circ}n=360^{\circ}\)
\(\implies n=\dfrac{360^{\circ}}{40^{\circ}}\)
\(\implies n=9\)
Therefore, the regular polygon has 9 sides.
To determine the length of each side, divide the given perimeter by the number of sides:
\(\implies \sf Side\;length=\dfrac{Perimeter}{\textsf{$n$}}\)
\(\implies \sf Side \;length=\dfrac{72}{9}\)
\(\implies \sf Side \;length=8\;ft\)
Therefore, the length of each side of the regular polygon is 8 ft.
\(\hrulefill\)
Question 3The area of a regular polygon can be calculated using the following formula:
\(\boxed{\begin{minipage}{5.5cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{s^2n}{4 \tan\left(\dfrac{180^{\circ}}{n}\right)}$\\\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\end{minipage}}\)
A regular pentagon has 5 sides, so n = 5.
If its perimeter is 50 inches, then the length of one side is 10 inches, so s = 10.
Substitute the values of s and n into the formula and solve for A:
\(\implies A=\dfrac{(10)^2 \cdot 5}{4 \tan\left(\dfrac{180^{\circ}}{5}\right)}\)
\(\implies A=\dfrac{100 \cdot 5}{4 \tan\left(36^{\circ}\right)}\)
\(\implies A=\dfrac{500}{4 \tan\left(36^{\circ}\right)}\)
\(\implies A=\dfrac{125}{\tan\left(36^{\circ}\right)}\)
\(\implies A=172.047740...\)
Therefore, the area of a regular pentagon with perimeter 50 inches is 172.0 in² rounded to the nearest tenth.
Answer:
1.695.29 m^2
2.8 feet
3. 172.0477 in^2
Step-by-step explanation:
1. The area of a regular octagon can be found using the formula:
\(\boxed{\bold{Area = 2a^2(1 + \sqrt{2})}}\)
where a is the length of one side of the octagon.
In this case, a = 12 m, so the area is:
\(\bold{Area = 2(12 m)^2(1 + \sqrt{2}) = 288m^2(1 + \sqrt2)=695.29 m^2}\)
Therefore, the Area of a regular octagon is 695.29 m^2
2.
The formula for the exterior angle of a regular polygon is:
\(\boxed{\bold{Exterior \:angle = \frac{360^o}{n}}}\)
where n is the number of sides in the polygon.
In this case, the exterior angle is 40°, so we can set up the following equation:
\(\bold{40^o=\frac{ 360^0 }{n}}\)
\(n=\frac{360}{40}=9\)
Therefore, the polygon has n=9 sides.
Perimeter=72ft.
We have
\(\boxed{\bold{Perimeter = n*s}}\)
where n is the number of sides in the polygon and s is the length of one side.
Substituting Value.
72 feet = 9*s
\(\bold{s =\frac{ 72 \:feet }{ 9}}\)
s = 8 feet
Therefore, the length of each side of the polygon is 8 feet.
3.
Solution:
A regular pentagon has five sides of equal length. If the perimeter of the pentagon is 50 in, then each side has a length = \(\bold{\frac{perimeter}{n}=\frac{50}{5 }= 10 in.}\)
The area of a regular pentagon can be found using the following formula:
\(\boxed{\bold{Area = \frac{1}{4}\sqrt{5(5+2\sqrt{5})} *s^2}}\)
where s is the length of one side of the Pentagon.
In this case, s = 10 in, so the area is:
\(\bold{Area= \frac{1}{4}\sqrt{5(5+2\sqrt{5})} *10^2=172.0477 in^2}\)
Drawing: Attachment

simplify 0.081*0.0098/0.0049*0.27
Answers
9514 1404 393
Answer:
0.04374
Step-by-step explanation:
A calculator is a useful tool for simplifying numerical expressions.
__
Since all of the operations are multiplication or division, you simply do them left to right.
0.081*0.0098/0.0049*0.27
= 0.0007938/0.0049*0.27
= 0.162*0.27
= 0.04374

The radius of a circle is 5 meters. What is the length of a 45° arc?
Answers
Answer:
Step-by-step explanation:

What's the exact value of sin 7π∕12



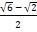
Answers
Answer:
(√2+√6) / 4
Step-by-step explanation:
sin (7π/12) = sin (3π/12 + 4π/12) = sin 3π/12 cos 4π/12 + cos 3π/12 sin 4π/12
==> sin π/4 cos π/3 + cos π/4 sin π/3
==> (1/√2)(1/2) + (1/√2)(√3/2)
==> (√6+√2) / 4
Find the original slope of (-6,-1) and (0,3)
Answers
Answer:
slope (m) = 2/3
Step-by-step explanation:
slope = change in x /change in y
Also, slope is y2 - y1 / x2 -x1. That is what I apply for this activity, hence:
slope = 3 - (-1) / 0 - (-6)
= 3 + 1 / 0 + 6
= 4 / 6
= 2/3
∴ slope(m) = 2/3