What is the general form of the equation for the given circle centered at o(0, 0)? a. x2 y2 41 = 0 b. x2 y2 − 41 = 0 c. x2 y2 x y − 41 = 0 d. x2 y2 x − y − 41 = 0
Answers
The general form of the equation for the given circle centered at o(0, 0) is x² + y² - 41 = 0.
According to the question,
The general form of the equation for the given circle centered at o(0, 0) is (x-h)² + (y-k)² = r².
The given equation is x² + y² - 41 = 0 which is also represented by(x-0)² + (y-0)² = -(√41)². This is not possible.
The given equation is x² + y² - 41 = 0 which is also represented by (x-0)² + (y-0)² = (√41)²This means that the circle is centered at (0,0). Thus, the equation is correct The given equation is x² + y² +x+ y- 41 = 0 which is also represented by (x+1/2)² + (y+1/2)² = (√(83/2))²This means that the circle is centered at (-1/2,-1/2). Thus, this equation is incorrect. The given equation is x² + y² +x- y- 41 = 0 which is also represented by (x+1/2)² + (y-1/2)² = (√(83/2))²This means that the circle is centered at (1/2,-1/2). Thus, this equation is incorrect.Hence, the general form of the equation for the given circle centered at o(0, 0) is x² + y² - 41 = 0.
Learn more about circle here
https://brainly.com/question/14338946
#SPJ1
Related Questions
The partially filled contingency table gives the frequencies of the data on age (in years) and sex from the residents of a retirement home. 60-69 70-79 Over 79 Total Male 1 9 5 Female 19 2 4 Total What is the probability that a resident is female ? Round your answer to three decimal places if necessary. a. 0.635 c. 0.62 b. 0.629 d. 0.625
Answers
The probability that a resident is female is 0.625.
Probability is a method for determining how likely something is to happen. Many things are difficult to forecast with absolute confidence. Using it, we can only make predictions about the likelihood of an event happening, or how likely it is.
We know that the probability of a function is the ratio of favorable cases to the total number of cases possible.
Given that,
Total number of females = 19+2+4 =25
total number of males=1+9+5 = 15
The probability that a resident is female is the Total number of females / total number of people
Hence total number of people = 25+15 = 40
So, Probability = 25/40 = 0.625
Therefore, the probability that a resident is female is 0.625.
To know more about probability visit: brainly.com/question/30034780
#SPJ4
The probability that a resident is female = 0.625
The correct answer is an option (d)
The complete contingency table would be:
60-69 70-79 Over 79 Total
Male 1 9 5 15
Female 19 2 4 25
Total 20 11 9 40
Here, sample space i.e., the total number of residents = 40
So, n(S) = 40
Let event A: a resident is female
From the contigency table, the number of favourable outcomes of the event A are 25
So, n(A) = 25
Using the definition of probability, the probability of event A would be,
p(A) = n(A)/n(S)
p(A) = 25/40
p(A) = 0.625
Therefore, the required probability is 0.625
Learn more about the probability here:
https://brainly.com/question/30034780
#SPJ4
Guys can you please help me with The Question #15 A). and B). of The Factoring for me, please? :)

Answers
Answer:
(a) width = (x - 1)
length = (7x - 6)
(b) Area = 350 cm²
Perimeter = 114 cm
Step-by-step explanation:
Part (a)Given equation: \(7x^2-13x+6\)
⇒ a = 7, b = -13, c = 6
Find 2 two numbers that multiply to ac and sum to b: -6 and -7
Rewrite b as the sum of these 2 numbers:
\(\implies 7x^2-7x-6x+6\)
Factorize the first two terms and the last two terms separately:
\(\implies 7x(x-1)-6(x-1)\)
Factor out the common term (x - 1):
\(\implies (7x-6)(x-1)\)
Therefore:
width = (x - 1)length = (7x - 6)Part (b)Substitute the given value of x = 8 into the equations to find the area and perimeter:
\(\begin{aligned}x=8cm \implies \textsf{Area} & = 7(8)^2-13(8)+6\\& = 448-104+6\\& = 350 \sf \:\: cm^2\end{aligned}\)
\(\begin{aligned}\textsf{Perimeter} & = 2(\sf width+length)\\& =2[(x-1)+(7x-6)]\\ & = 2[(8-1)+(7(8)-6)]\\ & = 2[7+(56-6)] \\& = 2(7+50)\\& = 2(57)\\ & = 114 \sf \:\: cm\end{aligned}\)
Answer:
See below ~
Step-by-step explanation:
\(\textsf {Question 15(A) :}\)
\(\textsf {Given :}\)
\(\implies \mathsf {7x^{2} - 13x + 6}\)
\(\textsf {Splitting the middle term :}\)
\(\implies \mathsf {7x^{2} - 7x - 6x + 6}\)
\(\textsf {Grouping common terms :}\)
\(\implies \mathsf {7x(x - 1) - 6(x - 1)}\)
\(\textsf {Dimensions are :}\)
\(\textsf {Length = (7x - 6)}\)\(\textsf {Width = (x - 1)}\)\(\textsf {Question 15(B) :}\)
\(\textsf {Formula for perimeter :}\)
\(\implies \mathsf {2 \times (length + width)}\)
\(\implies \mathsf {2 \times (7x - 6 + x - 1)}\)
\(\implies \mathsf {2 \times (8x-7)}\)
\(\textsf {Substitute x = 8 :}\)
\(\implies \mathsf {2 \times [8(8)-7]}\)
\(\implies \mathsf {2 \times (64-7)}\)
\(\implies \mathsf {2 \times 57}\)
\(\implies \mathsf {Perimeter = 114 cm}\)
\(\textsf {Now substitute x = 8 in the area formula :}\)
\(\implies \mathsf {7(8)^{2} - 13(8) + 6}\)
\(\implies \mathsf {7(64) - 104 + 6}\)
\(\implies \mathsf {448 - 98}\)
\(\implies \mathsf {Area = 350 cm^{2}}\)
HELP!!! Please solve the problem and give me the answer!!!

Answers
Answer:
answer A
Step-by-step explanation:
Hello,
\((fog)(x)=f(g(x))=f(2x-1)=3(2x-1)+14=6x-3+14=6x+11\)
so the correct answer is A.
hope this helps
Answer:
A. 6x + 11.
Step-by-step explanation:
(f o g)(x)
We replace the x in f(c) by g(x) and simplify:
= 3(2x - 1) + 14
= 6x - 3 + 14
= 6x + 11.
Hasan buys two kinds of cloth materials for school uniforms, shirt material that costs him ₹ 50 per metre and trousers material that costs him ₹ 90 per metre. For every 3 metres of the shirt material, he buys 2 metres of the trouser material. He sells the materials at 12% and 10% profit respectively. His total sale is ₹ 36,600. How much trouser material did he buy?
PLease i want it with step by step explanation
Answers
Answer:
Step-by-step explanation:
Let x represent the number of meters of shirt material that he bought.
Let y represent the number of meters of trouser material that he bought.
For every 3 metres of the shirt material, he buys 2 metres of the trouser material. It means that
2x = 3y
x = 3y/2
shirt material cost him ₹ 50 per metre and trousers material cost him ₹ 90 per metre. It means that the total cost is
50x + 90y
Selling price for the shirt material is
50x + (12/100 × 50x) = 56x
Selling price for the trouser material is
90y + (10/100 × 90y) = 99y
If his total sale is ₹ 36,600, it means that
56x + 99y = 36600- - - - - - - - 1
Substituting x = 3y/2 into equation 1, it becomes
56(3y/2) + 99y = 36600
Multiplying both sides by 2, it becomes
168y + 198y = 73200
366y = 73200
y = 73200/366
y = 200
x = 3y/2 = 3 × 200/2
x = 300
He bought 200 meters of trouser material
determine the quotient of 2/3 ÷ 4/5
Answers
Answer:
5/6
Step-by-step explanation:
It might make the problem easier to understand if we were to rewrite it as:
2
----
3
======
4
----
5
In this expression, we're dividing by a fraction, the fraction 4/5. We can get the same result by inverting this divisor fraction, 4/5, and then multiplying 2/3 by 5/4:
5 2
----- * -----
4 3
This reduces to
5 1
----- * ----- = 5/6
2 3
CAN SOMEONE PLS HELP ME ASAP!!!!
Find the volume of the new fish tank in the front office. The picture is below and thanks for your help

Answers
(i) Simplify
n²-(n+ a)(n-a).
(ii) Hence evaluate
326541 8292-326541833 x 326541 825.
Answers
Answer: 16
Step-by-step explanation:
\(n^2-(n+a)(n-a)=\\n^2-(n^2-a^2)=\\n^2-n^2+a^2=\\a^2\)
\(326541829^2-326541833*326541825=\\32654129^2-(32654129+4)(326541129-4)=\\4^2=\\4*4=\\16\)
If u, V, W are vectors and 0 is the zero vector; one of the following is not always true: points a. uX (vtw) =uXv+uXw b. (vtw) Xu =vXu+wXu c. v X u=uXv d. 0 X u = 0
Answers
Answer : One of the following statements is not always true: uX (vtw) =uXv+uXw, (vtw) Xu =vXu+wXu.
The statement, "one of the following is not always true: points a. uX (vtw) =uXv+uXw b. (vtw) Xu =vXu+wXu c. v X u=uXv d. 0 X u = 0," is correct. The first statement, "uX (vtw) =uXv+uXw," is false because in general, the distributive law does not apply to vector multiplication. This means that the left-hand side of the equation, "uX (vtw)," cannot be rearranged to "uXv+uXw."
The second statement, "(vtw) Xu =vXu+wXu," is also false because vector multiplication is not commutative; the order of the vectors in a multiplication equation matters. Therefore, "(vtw) Xu" is not equal to "vXu+wXu." The third statement, "v X u=uXv," is true because vector multiplication is commutative. This means that the order of the vectors in a multiplication equation does not matter.
The fourth statement, "0 X u = 0," is also true. The zero vector is a special type of vector whose components all equal 0. When any vector is multiplied by the zero vector, the result is always the zero vector.
In conclusion, one of the following statements is not always true: uX (vtw) =uXv+uXw, (vtw) Xu =vXu+wXu.
Know more about vector here:
https://brainly.com/question/13322477
#SPJ11
What is a counterexample for the conjecture? if the area of a rectangle is 80 square units, the perimeter must be greater than 35. 9 units.
Answers
if the area of a rectangle is 80 square units, the perimeter must be lesser than or equal to 35. 9 units.
What is a conjecture?
A conjecture is a conclusion or a proposition that is made tentatively and without supporting evidence.
The conjecture for the given question is:
if the area of a rectangle is 80 square units, the perimeter must be lesser than or equal to 35. 9 units.
Greater than → Lesser than or equal to
To learn more about area of rectangles.
https://brainly.com/question/24813201
#SPJ4
How do you know if a function is always positive?
Answers
There are a few different ways you can determine whether a function is always positive:
1. Analyze the function's formula: If the function's formula includes only positive terms or is a product of positive factors, it is likely that the function will be positive for all input values.
2. Graph the function: Plotting the function on the coordinate plane can give you a visual understanding of the function's behavior. If the graph always lies above the x-axis, the function is always positive.
3. Consider the function's domain: If the domain of the function consists only of positive numbers, the function will be positive for all input values in its domain.
4. Use the function's properties: If the function is increasing, continuous, and has no zeros in its domain, it will always be positive. Similarly, if the function is decreasing, continuous, and has no zeros in its domain, it will always be negative.
5. Test the function for specific input values: You can also test the function for specific input values to see if the output is always positive. For example, if the function is defined for all real numbers, you could test it for a few small positive and negative values to see if the output is always positive.
Thus, above mentioned are used to determine if a function is always positive.
To learn more about Positivity of a function,
visit; brainly.com/question/24112720
#SPJ4
Evaluate: -8/9 + 4/9 - 2/9
A. -14/9
B. -2/3
C. 10/9
D. -1/3
Answers
Answer:
-2/3
Step-by-step explanation:
Add the first two then subtract
The answer to the equation is B, \(-\frac{2}{3}\)
First, you must add the the fractions. You add the numerator because all three fractions have like denominators.
\(-\frac{8}{9} +\frac{4}{9} -\frac{2}{9}=\frac{6}{9}\)
Then, you must simplify \(-\frac{6}{9}\)
\(-\frac{6}{9} =-\frac{2}{3}\)
The answer to the equation is \(-\frac{2}{3}\)
Give the least common multiple: 3a, 15 _____
Answers
Answer:
Answer: LCM of 3 and 15 is 15. 2.
Step-by-step explanation:
Hope this helps
Can some help simplify this question, with positive exponents

Answers
Answer:
4\(a^{9}\)\(b^{8}\)
Step-by-step explanation:
\(\frac{8a^{6}b^{12} x 4a b^{3} }{8x^{-2}b^{7} }\)
\(\frac{32a^{7} b^{15} }{8a^{-2} b^{7} }\)
4\(a^{9}\)\(b^{8}\)
Helping in the name of Jesus.
You and your friend are trying to meet up at the park. You are currently 256 m directly west from the centre of the park. Your friend is currently 388 m directly north from the centre of the park. What is the distance between you and your friend?
Answers
Answer:
The distance between the two is 465 meters
Step-by-step explanation:
We first need to set up a triangle that shows the relative position and distances of the two friends
Please check attachment for this
To get this distance, which represents the hypotenuse of the triangle, we make use of Pythagoras’ theorem
Mathematically;
Pythagoras’ theorem states that the square of the hypotenuse equals the sum of the squares of the two other sides
Thus;
D^2 = 256^2 + 388^2
D^2 = 216,080
D = √216,080
D = 464.84 which is approximately 465 m

I GIVE BRAINIEST
Someone pls help me with number 3 and 4
But step by step pls

Answers
Answer:
The video is blocked for me
Step-by-step explanation:
Answer:
Step-by-step explanation:

The perimeter of an equilateral triangle is 15 x 30 units. which expression can be used to show the side length of one side of the equilateral triangle? 15 (x 2): each side length is x 2 units. 30 (one-half x 1): each side length is one-half x 1 units. 5 (3 x 6): each side length is 3 x 10 units. 3 (5 x 10): each side length is 5 x 10 units.
Answers
The length of one side of the equilateral triangle is 5x + 10 units
What is an equilateral triangle ?
An equilateral triangle is a triangle that has all of its sides equal. Let a, b and c be the sides of the equilateral triangle. Since all the sides are equal, then a = b = c.
The perimeter of the triangle is the sum of all the sides of the triangle.
P = a + b+ c
GIVEN THE PERIMETER OF THE EQUILATERAL TRIANGLE AS P = 15 x + 30 units and a = b = c, then;
15 x + 30 = a + b + c
15 x + 30 = a + a + a (since all sides are equal)
15 x + 30 = 3a
3a = 15 x + 30
3a = 3(5x+10)
Dividing both sides by 3 will give;
3a/3 = 3(5x+10)/3
a = 5x+10
Hence, the length of one side of the equilateral triangle is 5x + 10 units.
to know more about equilateral triangle , visit:
https://brainly.com/question/17264112
#SPJ4
A pot of boiling soup with an internal temperature of 100° Fahrenheit was taken off the stove to cool in a 68° F room. After 20 minutes, the internal temperature of the soup was 91° F. a. Use Newton's Law of Cooling to write a formula that models this situation. Round to four decimal places. T(t) = (Lett be time measured in minutes.) b. To the nearest minute, how long will it take the soup to cool to 70° F? It will take approximately minutes for the soup to cool to 70° F. c. To the nearest degree, what will the temperature be after 1.1 hours? After 1.1 hours, the soup's temperature will be about degrees. (Recall that t is measured in minutes.) A turkey is taken out of the oven with an internal temperature of 190° Fahrenheit and is allowed to cool in a 73° F room. After half an hour, the internal temperature of the turkey is 150° F. a. Use Newton's Law of Cooling to write a formula that models this situation. Round to four decimal places. T(t) = (Let t be time measured in minutes.) b. To the nearest degree, what will the temperature be after 55 minutes? After 55 minutes, the turkey's temperature will be about degrees. c. To the nearest minute, how long will it take the turkey to cool to 120° F? It will take approximately minutes for the turkey to cool to 120° F.
Answers
a) The formula that models this situation is: T(t) = 68 + 32\(e^{(-0.0152t)}\) .
b) To the nearest minute, it take 99 minutes for the soup to cool to 70° F.
c) To the nearest minute, it take 1.1 hours for the turkey to cool to 120° F.
a) Using Newton's Law of Cooling to model this situation we have:
T(t) = Troom + (T₀ - Troom)\(e^{(-kt)}\)
Where, T(t) is the temperature of the soup (or turkey) at time t
Troom is the room temperature
T₀ is the initial temperature k is a constant of proportionality
t is time measured in minutes
For the soup, we have:
T(t) = 68 + (100 - 68)\(e^{(-kt)}\)
After 20 minutes, the internal temperature of the soup was 91° F.
Therefore, when t = 20,
T(t) = 91.
Hence, we can substitute these values in the above equation and solve for k as follows:
91 = 68 + 32\(e^{(-20k)}\)
=> 23 = 32\(e^{(-20k)}\)
=> ln(23/32)
= -20k
=> k ≈ 0.0152
Therefore, the formula that models this situation is:
T(t) = 68 + 32\(e^{(-0.0152t)}\) (rounded to four decimal places)
b) To find the time it takes for the soup to cool to 70° F,
we need to solve the equation T(t) = 70.
Therefore:
70 = 68 + 32\(e^{(-0.0152t)}\)
=> 2 = 32\(e^{(-0.0152t)}\)
=> ln(1/16) = -0.0152t
=> t ≈ 98.60
Hence, it will take approximately 99 minutes for the soup to cool to 70° F. (rounded to the nearest minute)
c) 1.1 hours is equal to 66 minutes.
Therefore, to find the temperature of the soup after 1.1 hours, we need to evaluate T(66):
T(66) = 68 + 32\(e^{(-0.0152 \times 66)}\) ≈ 83.36
Therefore, after 1.1 hours, the soup's temperature will be about 83 degrees Fahrenheit. (rounded to the nearest degree)
For the turkey:
a) Using Newton's Law of Cooling to model this situation we have:
T(t) = Troom + (T₀ - Troom)\(e^{(-kt)}\)
Where, T(t) is the temperature of the turkey (or soup) at time t
Troom is the room temperature
T₀ is the initial temperature
k is a constant of proportionality
t is time measured in minutes
For the turkey, we have:
T(t) = 73 + (190 - 73)\(e^{(-kt)}\)
After half an hour, the internal temperature of the turkey was 150° F.
Therefore, when t = 30, T(t) = 150.
Hence, we can substitute these values in the above equation and solve for k as follows:
150 = 73 + 117\(e^{(-30k)}\)
=> 77 = 117\(e^{(-30k)}\)
=> ln(77/117) = -30k
=> k ≈ 0.0228
Therefore, the formula that models this situation is:
T(t) = 73 + 117\(e^{(-0.0228t)}\) (rounded to four decimal places)
b) To find the temperature of the turkey after 55 minutes, we need to evaluate T(55):
T(55) = 73 + 117\(e^{(-0.0228 \times 55)}\) ≈ 139.57
Therefore, after 55 minutes, the turkey's temperature will be about 140 degrees Fahrenheit. (rounded to the nearest degree)
c) To find the time it takes for the turkey to cool to 120° F,
we need to solve the equation T(t) = 120.
Therefore:120 = 73 + 117\(e^{(-0.0228t)}\)
=> 47 = 117\(e^{(-0.0228t)}\)
=> ln(47/117) = -0.0228t
=> t ≈ 92.61
Hence, it will take approximately 93 minutes for the turkey to cool to 120° F. (rounded to the nearest minute)
To know more about decimal places, visit:
https://brainly.com/question/20563248
#SPJ11
The sum of three numbers is 4. The second number is 1 more than twice the first. The sum of the first and third is –1. Find the numbers.
Answers
2nd condition: y = 2x + 1
3rd condition: x + z = - 1 <=> z = - x - 1
Based on the 2nd and 3rd, we replace the 1st as following:
x + 2x + 1 - x - 1 = 4 <=>
2x = 4 <=>
x = 2
Since x = 2, we solve the 2nd as following:
y = 2x + 1 <=>
y = 2*2 + 1 <=>
y = 4 + 1 <=>
y = 5
Same thing for the 3rd:
z = - x - 1 <=>
z = - 2 - 1 <=>
z = - 3
1. The first number is equal to 2.
2. The second number is equal to 5.
3. The third number is equal to -3.
Let the first number be a.Let the second number be b.Let the third number be c.Translating the word sentence into an algebraic expression, we have;
The sum of three numbers is 4:
\(a+b+c=4\) ....equation 1.
The second number is 1 more than twice the first:
\(b=2a+1\) ....equation 2.
The sum of the first and third is –1:
\(a+c=-1\) ....equation 3.
From eqn. 3, we have:
\(c=-1-a\) ....equation 4.
Substituting into eqn. 1, we have:
\(a+2a+1+(-1-a)=4\\\\3a+ 1-1-a=4\\\\2a=4\\\\a=\frac{4}{2}\)
a = 2
To find the value of b:
\(b=2a+1\\\\b=2(2)+1\\\\b=4+1\)
b = 5
To find the value of c:
\(c=-1-a\\\\c=-1-2\\\\\)
c = -3
Read more: https://brainly.com/question/16049
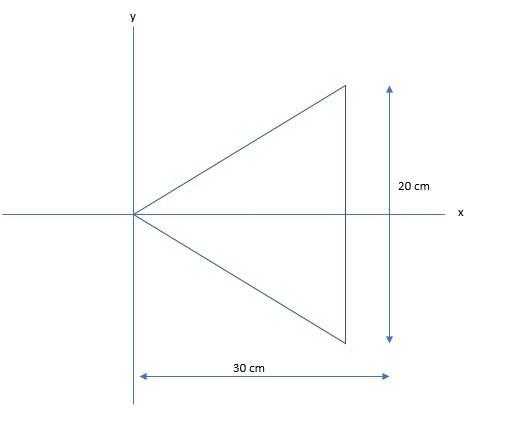
an 800 g steel plate has the shape of the isosceles triangle shown in the figure(figure 1).
Answers
The x- and y-coordinates of the center of mass are; (20, 0)
What is the center of mass of an object?The center of mass is the location where the sum of the relative position of the masses in a mass distribution is zero. It is the point where force can be applied on the distributed mass without causing a rotation of the system.
The mas of the steel plate = 800 g = 0.8 kg
The base length of the isosceles triangular plate = 20 cm = 0.2 m
The height of the isosceles triangular plate = 30 cm = 0.3 m
Considering a small strip of height, dx and width, I, we get
Area of small strip, dA = I·dx
Density of the plate for a unit thickness, ρ = M/A
Density of the small strip of mass dm = dm/dA
Considering the density of the plate as uniform, we get;
\(\displaystyle {\frac{dm}{dA} =\frac{M}{A}\)
Therefore;
\(\displaystyle {dm=\frac{M}{A}\times dA}\)
The area of the triangular plate, A = (1/2) × 0.2 m × 0.3 m = 0.03 m²
Mass of the plate, M = 0.8 kg
Therefore;
\(\displaystyle {dm=\frac{0.8}{0.03}\times I\cdot dx}\)
The width of the small strip, I, located at a distance x from the vertex of the triangular plate, using similar triangles, indicates;
\(\dfrac{I}{20} = \dfrac{x}{30}\)
\(I=20\times \dfrac{x}{30} = \dfrac{2}{3} \cdot x\)
Therefore;
\(\displaystyle {dm=\frac{0.8}{0.03}\times I\cdot dx} = \frac{0.8}{0.03}\times \dfrac{2}{3} \cdot x\cdot dx}\)
The center of mass, \(x_{cm}\), can be obtained with the formula; \(\displaystyle {x_{cm} = \dfrac{1}{M} \cdot \int\limits {x} \, dm }\)
Therefore; \(\displaystyle {x_{cm} = \dfrac{1}{0.8} \cdot \int\limits {x} \cdot \frac{0.8}{0.03} \cdot \frac{2}{3}\cdot x\, dx }\)
\(\displaystyle {x_{cm} = \dfrac{1}{0.8} \cdot \int\limits {x} \cdot \frac{0.8}{0.03} \cdot \frac{2}{3}\cdot x\, dx } = \dfrac{1}{0.8} \times \frac{0.8}{0.03} \times \frac{2}{3}\cdot \int\limits^3_0 {x^2} \, dx\)
\(\displaystyle {x_{cm} = \dfrac{1}{0.8} \times \frac{0.8}{0.03} \times \frac{2}{3}\cdot \int\limits^3_0 {x^2} \, dx = \frac{200}{9} \cdot \left[\frac{x^3}{3} \right]^{0.3}_0\)
\(\displaystyle {x_{cm} = \frac{200}{9} \cdot \left[\frac{x^3}{3} \right]^{0.3}_0=\frac{200}{9} \times \frac{0.027}{3} =0.2\)
The location of the x-coordinate center of mass, \(x_{cm}\) = 0.2 m = 20 cm from the vertex, which is the same location as the x-coordinate of the centroid of the plate of uniform density.
The plate is symmetrical about the x-axis, therefore, the y-coordinate of the center of mass is along the x-axis, which is \(y_{cm}\) = 0
The coordinate of the center of mass = (0.2, 0)
Part of the question requires the location of the coordinate of the center of mass of the triangular plate
Learn more about the center of mass of regular shapes here:
https://brainly.com/question/28021242
#SPJ1

eugheugh eughhhh I've been listening to my comfort playlist stressing about this test for too long Please just help ;-;

Answers
Answer:
1. Incorrect because it's suppose to be -4/5, -1/10, 7/10
2. Incorrect because it's suppose to be -7/8, -3/8, -3/4
3. Correct -2/3, -5/9, 2/9
4. Incorrect because it's suppose to be -4/7, -5/14, 6/7
What is the answer to 70 X 9 over 10
Answers
Explanation: 70x9=630 630 divided by 10=63
Answer:
63
Step-by-step explanation:
70x9=630, and that over 10 is the same as dividing it by ten, and 630 divided by 10 is 63
the weights of steers in a herd are distributed normally. the variance is 40,000 and the mean steer weight is 1400lbs . find the probability that the weight of a randomly selected steer is between 1580 and 1720lbs . round your answer to four decimal places.
Answers
Rounding to four decimal places, the probability is approximately 0.1293.
Given that the weights of steers in a herd are normally distributed with a mean (µ) of 1400 lbs and a variance (σ²) of 40,000 lbs², we first need to find the standard deviation (σ). We can do this using the formula:
σ = sqrt(σ²)
In this case, σ = sqrt(40,000) = 200 lbs.
Now, we need to find the z-scores for the weights 1580 lbs and 1720 lbs. The z-score formula is:
z = (X - µ) / σ
For 1580 lbs:
z1 = (1580 - 1400) / 200 = 0.9
For 1720 lbs:
z2 = (1720 - 1400) / 200 = 1.6
Next, we need to find the probability between these two z-scores. We can use a standard normal distribution table or calculator to find the probabilities corresponding to the z-scores:
P(z1) = P(Z ≤ 0.9) ≈ 0.8159
P(z2) = P(Z ≤ 1.6) ≈ 0.9452
Now, we'll subtract the probabilities to find the probability that the weight of a randomly selected steer is between 1580 and 1720 lbs:
P(0.9 ≤ Z ≤ 1.6) = P(Z ≤ 1.6) - P(Z ≤ 0.9) = 0.9452 - 0.8159 = 0.1293
To learn more about variance : brainly.com/question/13708253
#SPJ11
Find an equation of the circle that satisfies the stated conditions. (Give your answer in standard notation.) Center at the origin, passing through P(5, −8)
Answers
The equation of the circle that meets the specified requirements is x^2 + y^2 = 89, with the center at the origin and going through P(5, 8).
What is equation?In its most basic form, an equation is a mathematical statement that indicates that two mathematical expressions are equal. 3x + 5 = 14, for example, is an equation in which 3x + 5 and 14 are two expressions separated by a 'equal' sign. A mathematical phrase with two equal sides separated by an equal sign is called an equation. An example of an equation is 4 + 6 = 10.
Here,
The equation of a circle with center at the origin (0,0) and passing through the point (x1,y1) can be found using the distance formula.
The distance between a point (x1, y1) and the origin (0,0) is given by:
sqrt((x1-0)^2 + (y1-0)^2) = sqrt(x1^2 + y1^2)
Let's call the radius of the circle r. We know that the distance between the point (x1,y1) and the origin is equal to r. So, we can set up the equation:
sqrt(x1^2 + y1^2) = r
Substituting the values x1 = 5 and y1 = -8, we have:
sqrt(5^2 + (-8)^2) = r
Solving for r, we get:
r = sqrt(5^2 + (-8)^2) = sqrt(25 + 64) = sqrt(89)
Finally, we can write the equation of the circle in standard form using the center (0,0) and radius r:
(x - 0)^2 + (y - 0)^2 = r^2
x^2 + y^2 = r^2
x^2 + y^2 = 89
The equation of the circle that satisfies the stated conditions that is center at the origin, passing through P(5, −8) is x^2 + y^2 = 89.
To know more about equation,
https://brainly.com/question/2228446
#SPJ4
y= x2+8x+12 state one solution and one non-solution
Answers
Answer:
We will transform the equation to the vertex form:
y = x² + 8 x + 12 = x² + 8 x + 16 - 16 + 12 =
= ( x + 4 )² - 4
Vertex form is: y = a ( x - k )² + h
Vertex coordinates are: ( - 4, - 4 ).
Step-by-step explanation:
if u solve this ur cool

Answers
Answer: A rectangle is ALWAYS a parallelogram and not all parallelograms are rectangles. (ex. Rhombus, square are both parallelograms) So Ainsley is wrong.
Step-by-step explanation: Parallelograms is a quadrilateral shape with 2 pairs of parallel sides. So, a rectangle has to always be one.
Alice graphs the relationship between x, the number of years an athlete has been playing basketball, and y, their average number of baskets per game. Her graph goes through the points (8, 8) and (4, 5). Which equation represents the graph?
Answers
Answer: (8,8)
Step-by-step explanation: because, you just need to do the math
The equation of line is y = ( 3/4 )x + 2
What is an Equation of a line?
The equation of a line is expressed as y = mx + b where m is the slope and b is the y-intercept
And y - y₁ = m ( x - x₁ )
y = y-coordinate of second point
y₁ = y-coordinate of point one
m = slope
x = x-coordinate of second point
x₁ = x-coordinate of point one
The slope m = ( y₂ - y₁ ) / ( x₂ - x₁ )
Given data ,
Let the equation of line be represented as A
Now , the value of A is
Let the first point be P = P ( 8 , 8 )
Let the second point be Q = Q ( 4 , 5 )
Now , the slope of the line between the two points is
Slope m = ( y₂ - y₁ ) / ( x₂ - x₁ )
Substituting the values in the equation , we get
Slope m = ( 5 - 8 ) / ( 4 - 8 )
Slope m = -3/-4
Slope m = 3/4
Now , the equation of line is y - y₁ = m ( x - x₁ )
Substituting the values in the equation , we get
y - 8 = 3/4 ( x - 8 )
On simplifying the equation , we get
y - 8 = ( 3/4 )x - 6
Adding 8 on both sides of the equation , we get
y = ( 3/4 )x + 2
Therefore , the value of A is y = ( 3/4 )x + 2
Hence , the equation of line is y = ( 3/4 )x + 2
To learn more about equation of line click :
https://brainly.com/question/14200719
#SPJ2
What is the magnitude of ?
V
(9,-4)
Answers
Answer:
The magnitude is sqrt((-4)^2 + (-9)^2) = 9.85. The angle is atan(-9/-4) = 180 deg + 66 deg = 246 deg = -114 deg.
Step-by-step explanation:
hope it help
Answer:
9.85
Step-by-step explanation:
|v|= √9²+(-4)²
=√81+16
=√97
|v|= 9.85
Find the value of n in the equation below to make each statement true
(1.) 3^4 x 3^n = (3^5)^2
(2.) 7^12/7^3 = 7^n x 7^4
(3.) 13^n/13^25 = 13^0
Answers
Answer:
Step-by-step explanation:
1. n=6
2. n= no solution
3. n= no solution
PLEASE ANSWER!!!
Find the value of x in the triangle shown below.
X
106
42

Answers
something you should keep in mind is that all three angles in a triangle always add up to 180 degrees.
so, here, since you know the two other angles, you can find the third.
180 - 106 - 42 will give you the measure of that third angle.
your answer will be 32.
hope i helped, good luck!
Answer:
32
Step-by-step explanation:
as you triangle angle add up to 180 so you add 106 by 42 which gives you 148 then
you take 180 -148 which it will give you =32
The temperature rose 5 degrees from 6:00am to 12:00pm.
Answers
The average rate of change per hour in the temperature is 0.83 degrees.
What is the average rate of change per hourTo find the average rate of change per hour, we need to divide the total change in temperature by the number of hours over which the temperature changed.
The temperature rose by 5 degrees from 6:00 am to 12:00 pm, which is a period of 6 hours.
Therefore, the average rate of change per hour can be calculated as follows:
average rate of change per hour = total change in temperature / number of hours
So, we have
average rate of change per hour = 5 degrees / 6 hours
average rate of change per hour = 0.83 degrees/hour (rounded to two decimal places)
So, the average rate of change per hour is 0.83 degrees.
Read more about rate of change at
https://brainly.com/question/17131025
#SPJ1