What is the value of r

Answer:

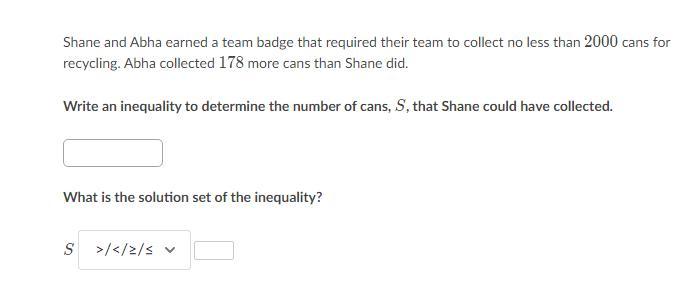
The inequalitty S-178<=2,000

Answer:

inverse it and do fx and gx inverse its value

The mathematical function that models Autumn's situation of saving $500 that she keeps at home and does not add to the savings is G(x) = 500 + 0x.

A mathematical function is an equation, expression, rule, or law defining the relationship between the independent variable and the dependent variable.

There are many types of mathematical function, including:

The amount that Autumn saved = $500

The amount that Autumn adds to the savings = $0

Let the number of periods that Autumn saves the above amount = x

G(x) = 500 + 0x

Thus, based on the linear function above, the amount that Autumn saved would remain $500 after many periods.

Learn more about mathematical functions at https://brainly.com/question/25638609.

#SPJ1

The amount of tax that is added to the cost of the computer is 159.72

From the question, we have the following parameters that can be used in our computation:

Computer cost = 968

Tax percentage = 16.5%

Using the above as a guide, we have the following:

Tax amount = Computer cost * Tax percentage

substitute the known values in the above equation, so, we have the following representation

Tax amount = 968 * 16.5%

Evaluate

Tax amount = 159.72

Hence, the amount of tax that is added to the cost of the computer is 159.72

Read more about sales tax at

https://brainly.com/question/9437038

#SPJ1

Answer:

9576

Step-by-step explanation:

Area of the triangle × height

(1/2×28×19)×36

Answer:

432000/135×100

Step-by-step explanation:

current house value is an increase of 35% oner the original value,

so if current value is 100% plus 35% or 135% of original value,

then original value is $432,000 / 135 x 100

Answer:

\(\begin{aligned}x &= 16\sqrt3 \\ &\approx 27.7\end{aligned}\)

Step-by-step explanation:

We can see that the longer leg (a) of a right triangle is half of the circle's radius. Since we are given the other two sides of the triangle (shorter leg and hypotenuse), we can solve for the length of the longer leg using the Pythagorean Theorem:

\(a^2 + b^2 = c^2\)

↓ plugging in the given values

\(a^2 + 2^2 = 14^2\)

↓ subtracting 2² from both sides

\(a^2 = 14^2 - 2^2\)

\(a^2 = 196 - 4\)

\(a^2 = 192\)

↓ taking the square root of both sides

\(a = \sqrt{192\)

↓ simplifying the square root

\(a = \sqrt{2^6 \cdot 3\)

\(a = 2^{\, 6 / 2} \cdot \sqrt3\)

\(a = 2^3\sqrt3\)

\(a = 8\sqrt3\)

Now, we can solve for the radius (x) using the fact that the longer leg of the triangle is half of it.

\(a = \dfrac{1}{2}x\)

↓ plugging in the a-value we solved for

\(8\sqrt3 = \dfrac{1}2x\)

↓ multiplying both sides by 2

\(\boxed{x = 16\sqrt3}\)

Using the Fundamental Counting Theorem, it is found that Kami could create 40,000 codes that start with an even number.

It is a theorem that states that if there are n things, each with \(n_1, n_2, \cdots, n_n\) ways to be done, each thing independent of the other, the number of ways they can be done is:

\(N = n_1 \times n_2 \times \cdots \times n_n\)

In this problem:

Hence:

\(N = 4 \times 10^4 = 40000\)

Kami could create 40,000 codes that start with an even number.

More can be learned about the Fundamental Counting Theorem at https://brainly.com/question/24314866

#SPJ1

Answer:

\( P(\bar X>2.8)\)

We can use the z score formula given by:

\( z=\frac{\bar X -\mu}{\frac{\sigma}{\sqrt{n}}}\)

And replacing we got:

\( z=\frac{2.8 -2.32}{\frac{1.24}{\sqrt{32}}}=2.190 \)

And using the normal standard distribution and the complement rule we got:

\( P(z>2.190 )= 1-P(z<2.190) = 1-0.986=0.014\)

Step-by-step explanation:

For this case w eknow the following parameters:

\( \mu = 2.32\) represent the mean

\(\sigma =1.24\) represent the deviation

n= 32 represent the sample sze selected

We want to find the following probability:

\( P(\bar X>2.8)\)

We can use the z score formula given by:

\( z=\frac{\bar X -\mu}{\frac{\sigma}{\sqrt{n}}}\)

And replacing we got:

\( z=\frac{2.8 -2.32}{\frac{1.24}{\sqrt{32}}}=2.190 \)

And using the normal standard distribution and the complement rule we got:

\( P(z>2.190 )= 1-P(z<2.190) = 1-0.986=0.014\)

Answer:

0.55% probability that the mean childhood asthma prevalence for the sample is greater than 2.8​%. This means that a sample having an asthma prevalence of greater than 2.8% is unusual event, that is, unlikely.

Step-by-step explanation:

To solve this question, we need to understand the normal probability distribution and the central limit theorem.

Normal probability distribution

When the distribution is normal, we use the z-score formula.

In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:

\(Z = \frac{X - \mu}{\sigma}\)

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

If X is more than two standard deviations from the mean, it is considered an unusual outcome.

Central Limit Theorem

The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).

For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

In this question, we have that:

\(\mu = 2.32, \sigma = 1.24, n = 43, s = \frac{1.24}{\sqrt{43}} = 0.189\)

What is the probability that the mean childhood asthma prevalence for the sample is greater than 2.8​%?

This is 1 subtracted by the pvalue of Z when X = 2.8. So

\(Z = \frac{X - \mu}{\sigma}\)

By the Central Limit Theorem

\(Z = \frac{X - \mu}{s}\)

\(Z = \frac{2.8 - 2.32}{0.189}\)

\(Z = 2.54\)

\(Z = 2.54\) has a pvalue of 0.9945

1 - 0.9945 = 0.0055

0.55% probability that the mean childhood asthma prevalence for the sample is greater than 2.8​%. This means that a sample having an asthma prevalence of greater than 2.8% is unusual event, that is, unlikely.

Solution :

Along the edge \($C_1$\)

The parametric equation for \($C_1$\) is given :

\($x_1(t) = 9t , y_2(t) = 0 \ \ for \ \ 0 \leq t \leq 1$\)

Along edge \($C_2$\)

The curve here is a quarter circle with the radius 9. Therefore, the parametric equation with the domain \($0 \leq t \leq 1 $\) is then given by :

\($x_2(t) = 9 \cos \left(\frac{\pi }{2}t\right)$\)

\($y_2(t) = 9 \sin \left(\frac{\pi }{2}t\right)$\)

Along edge \($C_3$\)

The parametric equation for \($C_3$\) is :

\($x_1(t) = 0, \ \ \ y_2(t) = 9t \ \ \ for \ 0 \leq t \leq 1$\)

Now,

x = 9t, ⇒ dx = 9 dt

y = 0, ⇒ dy = 0

\($\int_{C_{1}}y^2 x dx + x^2 y dy = \int_0^1 (0)(0)+(0)(0) = 0$\)

And

\($x(t) = 9 \cos \left(\frac{\pi}{2}t\right) \Rightarrow dx = -\frac{7 \pi}{2} \sin \left(\frac{\pi}{2}t\right)$\)

\($y(t) = 9 \sin \left(\frac{\pi}{2}t\right) \Rightarrow dy = -\frac{7 \pi}{2} \cos \left(\frac{\pi}{2}t\right)$\)

Then :

\($\int_{C_1} y^2 x dx + x^2 y dy$\)

\($=\int_0^1 \left[\left( 9 \sin \frac{\pi}{2}t\right)^2\left(9 \cos \frac{\pi}{2}t\right)\left(-\frac{7 \pi}{2} \sin \frac{\pi}{2}t dt\right) + \left( 9 \cos \frac{\pi}{2}t\right)^2\left(9 \sin \frac{\pi}{2}t\right)\left(\frac{7 \pi}{2} \cos \frac{\pi}{2}t dt\right) \right]$\)

\($=\left[-9^4\ \frac{\cos^4\left(\frac{\pi}{2}t\right)}{\frac{\pi}{2}} -9^4\ \frac{\sin^4\left(\frac{\pi}{2}t\right)}{\frac{\pi}{2}} \right]_0^1$\)

= 0

And

x = 0,  ⇒ dx = 0

y = 9 t,  ⇒ dy = 9 dt

\($\int_{C_3} y^2 x dx + x^2 y dy = \int_0^1 (0)(0)+(0)(0) = 0$\)

Therefore,

\($ \oint y^2xdx +x^2ydy = \int_{C_1} y^2 x dx + x^2 x dx+ \int_{C_2} y^2 x dx + x^2 x dx+ \int_{C_3} y^2 x dx + x^2 x dx $\)

                        = 0 + 0 + 0

Applying the Green's theorem

\($x^2 +y^2 = 81 \Rightarrow x \pm \sqrt{81-y^2}$\)

\($\int_C P dx + Q dy = \int \int_R\left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right) dx dy $\)

Here,

\($P(x,y) = y^2x \Rightarrow \frac{\partial P}{\partial y} = 2xy$\)

\($Q(x,y) = x^2y \Rightarrow \frac{\partial Q}{\partial x} = 2xy$\)

\($\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y} \right) = 2xy - 2xy = 0$\)

Therefore,

\($\oint_Cy^2xdx+x^2ydy = \int_0^9 \int_0^{\sqrt{81-y^2}}0 \ dx dy$\)

                            \($= \int_0^9 0\ dy = 0$\)

The vector field F is = \($y^2 x \hat i+x^2 y \hat j$\)  is conservative.

Answer:

The answer is C, x = 7.

Step-by-step explanation:

3x + 7 = 28

-7. -7

3x = 21

/3. /3

x = 7

From The question,

The daily supply of oxygen is provided by 625square feet lawn.

The total square feet of lawn supply daily = 11,875.

using comparison

625 sq ft provide oxygen for one organism

11875square ft will provide oxygen for Y-organism

11,875 square feet will supply oxygen for 19 organisms

The dimensions of the room are approximately 7 meters by 10.5 meters.

In Mathematics, dimensions are referred to as measures of size such as length, width, and height of an object or a shape. A rectangle has length and width as its dimensions that define the area of a rectangle.

Let's start by using algebra to represent the information given in the problem. Let x be the width of the rectangular room, then the length is 1.5 times the width or 1.5x.

The perimeter of a rectangle is the sum of the lengths of all its sides, which can be expressed as:

\(\text{Perimeter} = 2(\text{length} + \text{width})\)

Substituting the values we have for length and width, we get:

\(\rightarrow35 = 2(1.5\text{x} + \text{x})\)

Simplifying the equation, we get:

\(\rightarrow35 = 2(2.5\text{x})\)

\(\rightarrow35 = 5\text{x}\)

\(\rightarrow\text{x}=\dfrac{35}{5}\)

\(\rightarrow\bold{x\thickapprox7}\)

So the width of the room is 7 meters.

To find the length, we can substitute x into the expression we have for the length:

\(\rightarrow\text{Length} = 1.5\text{x}\)

\(\rightarrow\text{Length} = 1.5(7)\)

\(\rightarrow\bold{Length=10.5}\)

So the length of the room is 10.5 meters.

To know more about dimensions, click on:

https://brainly.com/question/31677552

Answer:

Median= (5+7)/2 = 6 Mean= 6 Range= 12 Mode=7

It's asking  would not be a solution soo

(-10, -9) as you can see

You're welcome thank me later

Answer:

4 kg of sugar would contain \( 1.2 \times 10^9 \) crystals.

Step-by-step explanation:

Given that 3kg of sugar contains 9 × 10⁸ crystals, let "x" represent the number of sugar crystals 4kg of sugar would contain.

Thus, set up a proportion as follows:

3 kg : 9 × 10⁸ = 4 kg : x

\( \frac{3}{9 \times 10^8} = \frac{4}{x} \)

Solve for x. Cross multiply.

\( 3 \times x = 9 \times 10^8 \times 4 \)

\( 3x = 36 \times 10^8 \)

\( 3x = 3.6 \times 10^9 \)

Divide both sides by 3

\( \frac{3x}{3} = \frac{3.6 \times 10^9}{3} \)

\( x = 1.2 \times 10^9 \)

4 kg of sugar would contain \( 1.2 \times 10^9 \) crystals.

The constant of proportionality in the equation c = 8m is 8.

A variation is a relation between a set of values of one variable and a set of values of other variables. Direct variation. In the equation y = mx + b, if m is a nonzero constant and b = 0, then you have the function y = mx (often written y = kx), which is called a direct variation.

since C = 8m is an equation and the relationship between c and m is direct.

It means that dividing both sides of the equation by m we have

C/m = 8m/m

c/m = 8

Therefore the constant of proportionality is 8

In conclusion the constant of proportionality for which c = 8m is 8.

Learn more about variation: https://brainly.com/question/6499629

#SPJ1

Answer:

That is the distributive property.

Answer:

distributive property

Answer: 90, 180, 270

Step-by-step explanation: 90 es divisible por todos esos números. Para obtener dos números más que sean divisibles por esos, simplemente multiplique 90 por 2 y 3.

The answer will be 0. 10 >  0. 01 . Option B

Given the values as;

Turn the values into proper fractions

a. 0. 10 = 10/ 100

Reduce to simpler terms

= 10/ 100

= 1/ 10

b. 0. 01 = 1/ 100

a = 1/ 100

b = 1/ 100

This means that both decimals are not of  equal proportion and thus a is greater than (>) b

Thus, the answer will be 0. 10 >  0. 01 . Option B

Learn more about decimals here:

https://brainly.com/question/1827193

#SPJ1

Answer:

#carryonlearning

Answer:

x-25

Step-by-step explanation:

25 less than x is equal to a number.

If we are trying to find this number (y for example), we need to set up an equation

y = 25 less than x

25 less than x is equal to x - 25

Answer:

Step-by-step explanation:

the dot would either (1,4) or (4,1)

a squared+ b squared= c squared

the length of the sides are 3

3 squared + 3 squared= c squared

9+9 =c squared

18= c squared

square root of 18 rounded to the nearest tenth is 4.2

Answer:

Step-by-step explanation:

Answer:

Step-by-step explanation:

$2.12 - $1.65 = $0.47
$0.47 x 65 = $30.55 profit.

This is an exercise in the formula to calculate the profits obtained from the sale of a product, it is an essential tool in the management of any business. By knowing the profits obtained from the sale of a product, business owners and managers can make informed decisions and adjust their business strategies to maximize their profitability.

Profit is calculated by subtracting the total costs of production from the total revenue earned from the sale of a product. Total production costs include not only the direct costs associated with manufacturing the product, but also indirect costs, such as advertising and marketing costs, the cost of packaging materials, and other overhead.

The total income obtained from the sale of a product is the product of the number of units sold by the sale price per unit. It is important to remember that the selling price per unit must be sufficient to cover both the direct and indirect costs of production, and to provide a reasonable profit.

Once the profit earned from the sale of a product has been calculated, business owners and managers can use this information to improve their profitability. If profits are low, they might consider lowering production costs, raising the selling price, or finding ways to sell more units. On the other hand, if profits are high, they might consider increasing their investment in advertising and marketing to attract more customers and expand their business.

In addition, profit calculation can also help business owners and managers assess the feasibility of launching a new product or expanding into new markets. By calculating total production costs and potential total revenue, they can determine if the new product or market is profitable and make informed decisions about whether to proceed with the launch or expansion.

The total cost of making the handles is the product of the number of handles times the cost per unit:

Total cost = 65 potholders × $1.65/potholder = $107.25

The total revenue from selling the handles is the product of the number of handles times the selling price per unit:

Total revenue = 65 potholders x $2.12/potholder = $137.8

Elmo's profit is the difference between total revenue and total cost:

Profit = Total Revenue - Total Cost

Profit = $137.8 - $107.25 = $30.55

Profit = $30.55