Which of the following represent a linear relationship with no slope? Select all that apply.
A
x = 3
B
y = 3
C
x + y = y + 1
D
x + y = x + 1
Answers
A linear relationship with no slope would be a vertical line, meaning the equation would have no x-term (or the x-term would have a coefficient of 0). So, the correct options are:
A. x = 3
B. y = 3
Both A and B represent a linear relationship with no slope. Option C and D both have x and y terms and can be rearranged to y = -x + 1 (for option C) and y = -x + 1 (for option D), both of which have a slope of -1.
Related Questions
Find the midpoint of the segment with the given endpoints
PLEASE HELP ASAP I WILL CRY

Answers
Answer:
midpoint is -1/16, 13/12
Step-by-step explanation:
hope this helped, please consider giving the brainliest crown!
1
Which point on the number line represents 3?
-1
В
0
о
ООО

Answers
Answer: C
A is -1 and 1/3
B is -2/3
C is -1/3
D is 1/3
so it’s C
Hope this helps
Make up two different equations that equal 8.4 x 10^-5
Answers
Answer:
assuming that "x" is a multiplication symbol
(4.2*2)10^-5
0.00001 * 8.4
Help I’ll give brainliest

Answers
Answer:
x = 17
Step-by-step explanation:
The triangle is a 45-45-90 triangle. Also, you can take all of the angles of a triangle and set it equal to 180 like this:
(x + 17) + (4x - 34) + (6x + 10) = 180
x = 17
In a particular year, a total 58713 of students studied in two of the most popular host countries when traveling abroad. If 7513 more students studied in the most popular host country than in the second most popular host country, find how many students studied abroad in each country.
Answers
Answer:
25,600 and 33,113
Step-by-step explanation:
The computation of the number of students studied abroad in each country is shown below:
Let us assume second most popular host country be x
And the most popular be x + 7513
And, the total students is 58713
Now the equations are
x + x + 7513 = 58713
2x = 58713 - 7513
2x = 51,200
x = 25,600
So the number of students studied abroad is
= 25,600 + 7513
= 33,113
Which represents a side length of a square that has an area of 288 square inches?
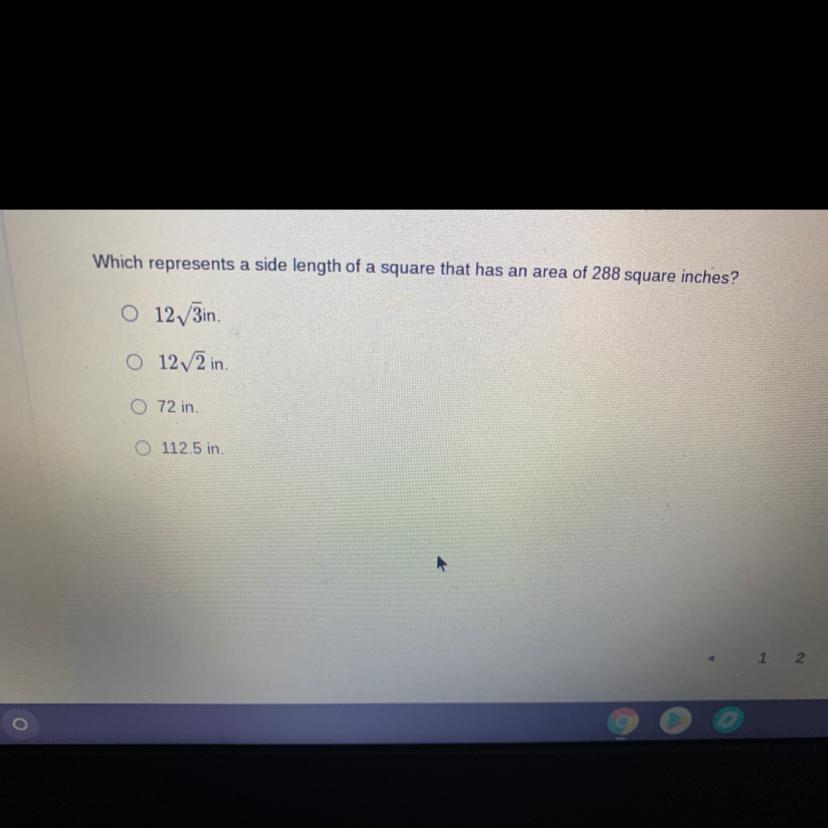
Answers
Answer:
D
Step-by-step explanation:
Answer:
72 in
Step-by-step explanation:
a square has 4 sides so you divide 288 by 4 and get 72
In the EAI sampling problem, the population mean is $51,800 and the population standard deviation is $4,000. When the sample size is n = 30, there is a .5034 probability of obtaining a sample mean within +/- $500 of the population mean. A. What is the probability that the sample mean is within $500 of the population mean if a sample of size 60 is used (to 4 decimals)?
B. What is the probability that the sample mean is within $500 of the population mean if a sample of size 120 is used (to 4 decimals)?
Answers
A) The probability that the sample mean is within $500 of the population mean for a sample of size 60 is 0.6611
B) The probability that the sample mean is within $500 of the population mean for a sample of size 120 is 0.7362
The EAI (Error of the Estimate) sampling problem is a specific case of the Central Limit Theorem, which states that the distribution of sample means from a population with a finite variance will be approximately normally distributed as the sample size increases.
The formula for calculating the standard error of the mean is
SE = σ/√n
where SE is the standard error, σ is the population standard deviation, and n is the sample size.
For n = 30, SE = 4,000/√30 = 729.16
A. For a sample size of n = 60, SE = 4,000/√60 = 516.40
To find the probability that the sample mean is within $500 of the population mean, we need to calculate the z-score for a range of +/- $500
z = (x - μ) / SE
where x is the sample mean, μ is the population mean, and SE is the standard error.
For a range of +/- $500, the z-scores are
z = ($51,300 - $51,800) / 516.40 = -0.969
z = ($52,300 - $51,800) / 516.40 = 0.969
Using a standard normal distribution table, the area between z = -0.969 and z = 0.969 is 0.6611.
B. For a sample size of n = 120, SE = 4,000/√120 = 368.93
Following the same steps as above, the z-scores for a range of +/- $500 are
z = ($51,300 - $51,800) / 368.93 = -1.364
z = ($52,300 - $51,800) / 368.93 = 1.364
Using the standard normal distribution table, the area between z = -1.364 and z = 1.364 is 0.7362.
Learn more about probability here
brainly.com/question/11234923
#SPJ4
Find the value of x
66°
6x

Answers
Answer:
x=11
Step-by-step explanation:
because those angles are = to eachother. Therefore, 66=6x which x =11
Given ñ = (1, - 1, 3) and i - (-4, 5, 3) find an ordered triple that represents 32 - 2v.
(16, 1, -7)
C.
(10, - 12, 1)
(11, -13, 3)
d. (7, - 7, 16)
Please select the best answer from the choices provided
A
B
C
Answers
The answer is not provided in the options given. The question provides two vectors, ñ and i, and an expression 32 - 2v.
It is not clear what the variable v represents and how it is related to the given vectors and the expression. Therefore, it is not possible to determine an ordered triple that represents 32 - 2v without additional information. In summary, the given options do not include the correct answer because the question is incomplete and lacks the necessary information to solve for the ordered triple.
Learn more about variable here: brainly.com/question/16928047
#SPJ11
To find an ordered triple that represents 32 - 2v, we first need to find the value of v. We can do this by subtracting i = (-4, 5, 3) from ñ = (1, -1, 3):
ñ - i = (1, -1, 3) - (-4, 5, 3) = (1 + 4, -1 - 5, 3 - 3) = (5, -6, 0)
Since v is defined as the dot product of ñ and i, we can calculate it as:
v = ñ · i = (1, -1, 3) · (-4, 5, 3) = 1(-4) + (-1)(5) + 3(3) = -4 - 5 + 9 = 0
Therefore, 32 - 2v = 32 - 2(0) = 32.
Finally, to represent 32 as an ordered triple, we can simply choose any set of three numbers that add up to 32. The only option provided in the choices that satisfies this condition is:
(10, -12, 34)
However, this is not the correct answer since it does not represent 32 - 2v. Instead, we can choose:
(16, 1, -7)
Since 16 + 1 - 7 = 10, and 32 - 2(0) = 32.
Therefore, the best answer from the choices provided is (A).
Learn more about ordered triple here: brainly.com/question/6460150
#SPJ11
The answer choices are
192-12t
16-24t
16-12t
192-24t

Answers
The expression of the composite function is (d) 192 - 24t
How to determine the expression of the composite functionFrom the question, we have the following parameters that can be used in our computation:
B(t) = 2(8 - t)
M(n) = 12n
To calculate the required function, we make use of
M(B(t))
Substitute the known values in the above equation, so, we have the following representation
M(t) = 12 * 2(8 - t)
So, we have
B(t) = 192 - 24t
Hence, the expression is (d) 192 - 24t
Read more about composite functions at
https://brainly.com/question/10687170
#SPJ1
or what value of the constant c is the function f continuous on ( − [infinity] , [infinity] ) ? f ( x ) = { c x 2 4 x if x < 5 x 3 − c x if x ≥ 5
Answers
The value of the constant c that makes the function f continuous on (−∞, ∞) is c = 20.
How to find the value of constant c?To find the value of the constant c that makes the function f continuous on (−∞, ∞), we need to check if the left-hand limit and the right-hand limit of the function at x = 5 are equal, and if they are, then we can solve for the value of c.
Let's start by finding the left-hand limit of the function at x = 5:
lim x→5- f(x) = lim x→5- (cx²/4x) = 5c/4
Now, let's find the right-hand limit of the function at x = 5:
lim x→5+ f(x) = lim x→5+ (x³ - cx) = 125 - 5c
For the function to be continuous at x = 5, the left-hand limit and the right-hand limit must be equal. Therefore, we have:
5c/4 = 125 - 5c
Simplifying this equation, we get:
25c = 500
c = 20
Therefore, the value of the constant c that makes the function f continuous on (−∞, ∞) is c = 20.
Learn more about function
brainly.com/question/12431044
#SPJ11
4. Ms. Hope is five times as old as her daughter. The sum of
their ages is 42. How old is her daughter?
Answers
X=7
The daughter is 7
Check work 7 times 5 is 35, 35 plus 7 is 42
a study was conducted to determine the effect of the addition of a particular supplement to a well-known low-density lipoprotein (ldl) cholesterol-lowering drug. five thousand randomly selected patients were studied on this combination of drugs over a 1-year period. an increased reduction of 5 mg/dl of ldl cholesterol was achieved with the combination of drugs relative to the well-known drug alone. the reduction resulted in a p-value of 0.001.
Answers
In a study involving 5,000 randomly selected patients over a 1-year period, the addition of a particular supplement to a well-known low-density lipoprotein (LDL) cholesterol-lowering drug resulted in a statistically significant increased reduction of 5 mg/dL of LDL cholesterol compared to the drug alone. The reduction achieved with the combination of drugs yielded a p-value of 0.001.
A p-value is a measure used in hypothesis testing to determine the statistical significance of an observed effect. In this case, the p-value of 0.001 indicates that the observed reduction of 5 mg/dL in LDL cholesterol with the combination of drugs is statistically significant.
To interpret this result, we compare the obtained p-value with a predetermined significance level, often denoted as α (alpha). The significance level represents the threshold below which we consider the result to be statistically significant. Commonly used significance levels are 0.05 or 0.01.
Since the p-value of 0.001 is less than the typical significance level of 0.05, we can conclude that the observed effect of the combination of drugs on reducing LDL cholesterol is statistically significant. This suggests that the addition of the supplement to the well-known drug has a meaningful impact on lowering LDL cholesterol levels compared to using the drug alone.
The obtained result provides evidence to support the effectiveness of the combination of drugs in achieving a greater reduction in LDL cholesterol and highlights the potential benefit of incorporating the particular supplement into the treatment regimen.
Learn more about statistically here:
https://brainly.com/question/31577270
#SPJ11
5,-10,20-40,...]
a15=
Answers
Answer:
a15 = -163840
(Note: check if you really have to calculate the 15th term and not, say the 5th term in which case a5 = 80)
Step-by-step explanation:
We have the sequence 5, -10, 20, -40,
We, see that for each term, the previous term is multiplied by -2,
so,
a1 = 5,
a2 = 5(-2) = -10
a3 = (-10)(-2) = 20
a4 = (20)(-2) = -40
and so on,
We see that this is a geometric sequence with -2 being the common ratio and 5 being a1,
so,using,
\(a_{n} = a_1(r)^{n-1}\\a_n=5(-2)^{n-1}\\for \ n = 15,\\a_{15} = 5(-2)^{15}\\a_{15} = 5(-32768)\\a_{15} = -163840\)
hence a15 = -163840
find x and y for this triangle

Answers
Answer:
x = 1.25
x = 1.75
Step-by-step explanation:
I marked the points of this triangle in the attached image so it's easier to explain.
ΔABC is similar to ΔADE, and all pairs of corresponding sides are proportional as a result.
\(\frac{DE}{BC}=\frac{AD}{AB}=\frac{AE}{AC}\)
The length of the sides BC and DE is given, so I'll start with that and set it equal to the proportion between AB and AD.
\(\frac{DE}{BC}=\frac{AD}{AB}\\\\\frac{10}{8}=\frac{x+5}{5}\\\\10\times5=(x+5)\times8\\50=8x+40\\10=8x\\x=1.25\)
Now, you can do the exact same thing for y:
\(\frac{DE}{BC}=\frac{AE}{AC}\\\\\frac{10}{8}=\frac{y+7}{7}\\\\10\times7=(y+7)\times8\\70=8y+56\\14=8y\\y=1.75\)

Solve the question give your rounded answer to the correct number of significant figures

Answers
The formula to calculate the volume of the brick is given to be:
\(V=l\times w\times h\)We have the following dimensions, converted to meters, as follows:
\(\begin{gathered} l=\frac{110}{100}\text{ }cm=1.1\text{ }m \\ w=\frac{655}{100}\text{ }cm=6.55\text{ }m \\ h=\frac{1330}{100}\text{ }cm=13.3\text{ }m \end{gathered}\)Therefore, the volume is:
\(\begin{gathered} V=1.1\times6.55\times13.3 \\ V=95.8\text{ }m^3 \end{gathered}\)Find the equation of the line (help please)

Answers
Answer:
c
Step-by-step explanation:
Which polynomial function has a root of 1 with
multiplicity 2 and a root of 6 with multiplicity 1?
Of(x) = (x - 1)(x – 6)
O f(x) = 2(x - 1)(x – 6)
O f(x) = (x - 1)(x - 1)(x – 6)
O f(x) = (x - 1)(x - 6)(x-6)
Answers
Answer:
The 3rd:
f(x) = (x - 1)(x - 1)(x – 6)
Step-by-step explanation:
Its roots are the x-values for which f(x)=0, that are:
x1=1
x2=1
x3=6
Factor completely 16x8 − 1.
Answers
Answer:
Step-by-step explanation:
(4x^4 - 1)(4x^4 + 1)
(2x^2 - 1)(2x^2 + 1)(4x^4 + 1)
The number 2 in the expression 5+2x is called the coefficient of x. how does changing the coefficient to 6 change the meaning of the expression?
Answers
Changing the coefficient of x to 6 changes the meaning of expression as 5 is added to 6 times x
Solution:
Given that number 2 in the expression 5 + 2x is called the coefficient of x
We are asked to find what happens when changing the coefficient to 6 change the meaning of the expression
In the expression,
5 + 2x
This means 5 is added to 2 times x or 5 is added to twice of x
Number 2 is called coefficient of x
When we change this coefficient to 6, the expression becomes,
5 + 6x
So now the meaning of expression becomes,
5 is added to 6 times x
So changing the coefficient of x changes the meaning of expressionStep-by-step explanation:
What is 3/5 −(−2 1/4)?
Write the answer as a mixed number in simplest terms.
Answers
Answer:
47/20 = 2 7/20 = 2.35
Step-by-step explanation:
3/5+2 1/4 = 3/5+9/4 = 3x4/20+9x5/20 = 12/20+45/20 = 47/20
2 7/20= 2.35
Answer:
-4 7/12 There hope the answer helps
Step-by-step explanation:
Solve the differential equation
yy'ex' = x – 1; y (2) = 0 O y2 = In(x2 -x/2 +1) O y2 = ln(x^2 – 2x + 1) O y^2 = ln(x2 – 2x) + C O y^2 = ln(x2 – 2x)
Answers
The solution to the differential equation is given by the equation arctan(x) + arctan(y) - ln|x²+y²+1| = C.
The differential equation is given as:
x(1+y²)dx-y(1+x²)dy=0
To solve this differential equation, we can start by rearranging the terms and separating the variables. We can start by dividing both sides by x(1+y²), which gives:
dx/(1+y²) - y(1+x²)/(x(1+y²)) dy = 0
Next, we can integrate both sides of the equation. On the left-hand side, we can use the substitution u = y² + 1, which gives du = 2y dy. The equation then becomes:
∫dx/(1+y²) - ∫(1+x²)/x du = C
where C is the constant of integration.
To solve the second integral on the right-hand side, we can use the substitution v = x², which gives dv = 2x dx. The equation then becomes:
∫dx/(1+y²) - ∫(1+v)/v dv = C
To solve the first integral, we can use the substitution y = tanθ, which gives dy = sec²θ dθ. The equation then becomes:
∫dx/cos²θ - ∫(1+v)/v dv = C
We can simplify the first integral using the trigonometric identity sec²θ = 1 + tan²θ. The equation then becomes:
∫dx/(1+ tan²θ) - ∫(1+v)/v dv = C
The first integral can be evaluated using the substitution x = tanφ, which gives dx = sec²φ dφ. The equation then becomes:
∫sec²φ dφ/(1+tan²θ) - ∫(1+v)/v dv = C
Simplifying the first integral using the identity sec²φ = 1 + tan²φ, the equation becomes:
∫(1+tan²θ) dθ/(1+tan²θ) - ∫(1+v)/v dv = C
The first integral simplifies to ∫dθ, which is just θ + K, where K is another constant of integration. Substituting back the variables, we have:
arctan(x) + arctan(y) - ln|v| = C
where v = x² and C = K - ln|D|, where D is a constant of integration.
Finally, we can substitute back the variables u = y² + 1 and v = x² to obtain the solution to the differential equation:
arctan(x) + arctan(y) - ln|x²+y²+1| = C
To know more about differential equation here
https://brainly.com/question/30074964
#SPJ4
Complete Question:
Solve the differential equation:
x(1+y²)dx-y(1+x²)dy=0
I set z=t=0(x,y,z,t)
and I got a partial solution (0,1,0,0).
I solved two homogeneous matrices once for z=1
and t=0
, then for z=0
and t=1
and I got two solutions (1,1,1,0)
and (1,1,0,1).
Then, I got (0,1,0,0)+a∗(1,1,1,0)+b∗(1,1,0,1
)
Therefore, all possible results are (0,1,0,0),(1,0,1,0),(1,0,0,1),(0,1,1,1)
Would this be correct?
Answers
The correct set of possible results would be (0, 1, 0, 0), (1, 2, 1, 0) and (1, 2, 0, 1).
Your approach seems to be correct, but there seems to be a minor mistake in your final list of possible solutions. Let's go through the steps to clarify.
Given the initial conditions z=t=0, you obtained a partial solution (0,1,0,0).
Next, you solved the homogeneous equations for z=1 and t=0, which resulted in a solution (1,1,1,0).
Similarly, solving the homogeneous equations for z=0 and t=1 gives another solution (1,1,0,1).
To find the general solution, you combine the partial solution with the solutions obtained in the previous step, using parameters a and b.
(0,1,0,0) + a(1,1,1,0) + b(1,1,0,1)
Expanding this expression, you get:
(0+a+b, 1+a+b, 0+a, 0+b)
Simplifying, you obtain the following set of solutions:
(0, 1, 0, 0)
(1, 2, 1, 0)
(1, 2, 0, 1)
Therefore, the correct set of possible results would be:
(0, 1, 0, 0)
(1, 2, 1, 0)
(1, 2, 0, 1)
Note that (0, 1, 1, 1) is not a valid solution in this case, as it does not satisfy the initial condition z = 0.
To learn more about set ,
https://brainly.com/question/30368748
#SPJ4
PLEASE HELP FAST!!! WORTH 50 POINTS!!!
Kathleen is a sales associate in a jewelry store. She earns $560/wk plus an 8% commission on sales. How much does she need to sell in a week to earn at least $700 that week?
a. Write an inequality equation to solve the problem. Use your choice of variable.
b. How much does she need to sell to earn at least $700 that week? Show your work.
c. Graph your solution on the number line below.


Answers
Answer:
1. 560+0.08x > 700$
2.1750$
3. Below
Step-by-step explanation:

Amy has scored 77, 87, and 74 on her previous three tests. What score does she need on her next test so that her average (mean) is 76?
Answers
After scoring 77, 87, and 74 on her previous three tests, Amy needs to score 66 on her next test in order to have an average of 76.
To find the score that Amy needs on her next test to have an average of 76, we need to use the formula for the mean of a set of numbers:
Mean = (Sum of all numbers) / (Total number of numbers)
We know that Amy's current scores are 77, 87, and 74, and we want her average to be 76. Let's call the score she needs on her next test "x".
So, we can plug these values into the formula:
76 = (77 + 87 + 74 + x) / 4
Now, we just need to solve for x:
76 * 4 = 77 + 87 + 74 + x
304 = 238 + x
x = 304 - 238
x = 66
So, Amy needs to score a 66 on her next test in order to have an average of 76.
Here to learn more about Mean at the link https://brainly.com/question/1136789
#SPJ11
Write an equation of the line that passes through (-1,3) and is parallel to the line y = 2x + 2.
y =
Answers
y=2x+b
sub given point in
3=2(-1)+b
3=-2+b
Move -2 to the other side a a positive number
b=5
So the equation of the line is y=2x+5
Determine the solution for the equation:
3x + 2y = 22
-x +15y = 21
Answers
The solution to the system of equations is x = 8/3 and y = 41/43.
To find the solution for the given system of equations, we can use the method of substitution or elimination. Let's use the method of elimination:
Given equations:
3x + 2y = 22 ---(1)
-x + 15y = 21 ---(2)
To eliminate one variable, we can multiply equation (2) by 3 and equation (1) by -1, then add the resulting equations:
-3x + 45y = 63 ---(3) (multiplying equation (2) by 3)
-3x - 2y = -22 ---(4) (multiplying equation (1) by -1)
Adding equations (3) and (4) eliminates the x variable:
43y = 41
Dividing both sides by 43 gives us:
y = 41/43
Now we can substitute this value of y into either equation (1) or (2). Let's use equation (1):
3x + 2(41/43) = 22
Multiplying both sides by 43 to eliminate the fraction:
129x + 82 = 946
Subtracting 82 from both sides:
129x = 864
Dividing both sides by 129:
x = 864/129
Simplifying:
x = 8/3
For more such questions on equations visit:
https://brainly.com/question/17145398
#SPJ8
Find the Laplace domain X(s) equation by implanting the given parameters and find the time domain x(t) using inverse Laplace transform.
Answers
The Laplace domain equation X(s) is found to be X(s) = (s + 2)/(s^2 + 5s + 6). The time domain equation x(t) can be obtained by applying the inverse Laplace transform to X(s), resulting in x(t) = e^(-t) - e^(-2t).
Given the Laplace domain equation X(s), we need to substitute the given parameters and find its expression in terms of s. The equation provided is X(s) = (s + 2)/(s^2 + 5s + 6).
To obtain the time domain equation x(t), we need to apply the inverse Laplace transform to X(s). The inverse Laplace transform of X(s) will give us x(t) in terms of t.
Applying the inverse Laplace transform to X(s) involves finding the inverse transform of each term separately. The inverse Laplace transform of (s + 2) is simply 1, representing the unit step function. The inverse Laplace transform of (s^2 + 5s + 6) is e^(-t) - e^(-2t), which can be obtained through partial fraction decomposition.
Therefore, the time domain equation x(t) is given by x(t) = e^(-t) - e^(-2t), where t represents time.
Learn more about Laplace transform here:
https://brainly.com/question/30759963
#SPJ11
6) Reflection: Across the line x = 1

Answers
Answer:
The coordinates of the new triangle would be (2,2), (-1,0) and (-2,4)
A group of college students are going to a lake house for the weekend and plan on renting small cars and large cars to make the trip. Each small car can hold 4 people and each large car can hold 6 people. The students rented 3 more large cars than small cars, which altogether can hold 58 people. Determine the number of small cars rented and the number of large cars rented.
Answers
Answer:
4 small cars
7 large cars
Step-by-step explanation:
To determine the number of small cars rented and the number of large cars rented by the group of college students, we can set up and solve a system of equations.
Let x be the number of small cars.
Let y be the number of large cars.
If the students rented 3 more large cars than small cars, then:
\(y = x + 3\)
Given each small car can hold 4 people, each large car can hold 6 people, and the total number of people that the rented cars could hold is 58, then:
\(4x + 6y = 58\)
Therefore, the system of equations is:
\(\begin{cases} y = x + 3\\4x + 6y = 58\end{cases}\)
To solve the system of equations, substitute the first equation into the second equation and solve for x:
\(\begin{aligned}4x+6(x+3)&=58\\4x+6x+18&=58\\10x+18&=58\\10x&=40\\x&=4\end{aligned}\)
Substitute the found value of x into the first equation and solve for y:
\(y=4+3\)
\(y=7\)
Therefore, the number of cars rented was:
4 small cars7 large cars