Write an equation to show the total length of the bandages if they are placed end-to-end
There is an image attached btw

Answers
The equation that can be written to show the total length of the bandages if they are placed end-to-end is expressed as: 2(5/4) + 6/4 + 3(7/4) + 4(2) + 6(3).
How to Write an Equation for the Total Length?In the image given above that shows a line plot for the set of data representing the length of bandages, we have:
Two 1¼ = 2(5/4)
One 1 2/4 = 6/4
Three 1¾ = 3(7/4)
Four 2 = 4(2)
Six 3 = 6(3)
Thus, the equation that will represent the total length of the bandages can be expressed as:
2(5/4) + 6/4 + 3(7/4) + 4(2) + 6(3)
Learn more about equation on:
https://brainly.com/question/31521223
#SPJ1
Related Questions
Which one is greater1.22 or 1.02
Answers
Answer:
1.22 is greater
Step-by-step explanation:
everything after the decimal point is still the same as if it was a regular number. It's like comparing 22 and 02.
You can do 1.22-1.02 without getting a negative number
But when you do 1.02-1.22 the answer is -0.2.
I hope I could help!
Find the surface area of the composite solid.
A.
502 m2
B.
574 m2
C.
646 m2
D.
720 m2

Answers
Answer:
A is the answer I pretty sure
Answer:
i think the answer is 502 m2
The angle
�
1
θ
1
theta, start subscript, 1, end subscript is located in Quadrant
III
IIIstart text, I, I, I, end text, and
cos
(
�
1
)
=
−
5
8
cos(θ
1
)=−
8
5
cosine, left parenthesis, theta, start subscript, 1, end subscript, right parenthesis, equals, minus, start fraction, 5, divided by, 8, end fraction. What is the value of
sin
(
�
1
)
sin(θ
1
)sine, left parenthesis, theta, start subscript, 1, end subscript, right parenthesis?
Express your answer exactly. Sin
(
�
1
)
=
sin(θ
1
)=sine, left parenthesis, theta, start subscript, 1, end subscript, right parenthesis, equals
Answers
The value of sin(θ1) can be found using the Pythagorean identity, which states that sin2(θ) + cos2(θ) = 1. We can rearrange this equation to solve for sin(θ):
sin2(θ) = 1 - cos2(θ)
Taking the square root of both sides gives us:
sin(θ) = √(1 - cos2(θ))
We are given that cos(θ1) = -5/8, so we can substitute this value into the equation:
sin(θ1) = √(1 - (-5/8)2)
Simplifying the expression inside the square root gives us:
sin(θ1) = √(1 - 25/64)
sin(θ1) = √(39/64)
Taking the square root of the fraction gives us:
sin(θ1) = √39/8
Since the angle θ1 is located in Quadrant III, where sine values are negative, we need to take the negative of this value:
sin(θ1) = -√39/8
Therefore, the value of sin(θ1) is -√39/8.
Learn more about Pythagorean
brainly.com/question/24252852
#SPJ11
The graph of a function is a line that passes through the points (3, 17) and (6, 32). How would you find the rate of change for the function?
A. 3−6/17−352
B. 6−3/32−17
C. 32−6/17−3
D. 32−17/6−3
Answers
Answer:
D
Step-by-step explanation:
The rate of change is equal to m, the slope =
rise / run = (32-17) / (6-3)
Find magnitude of theta. Was told two major things are triangle angles equal 180 and alternate interior angles.

Answers
The measure of the angle θ is 30 degrees, or the magnitude of theta is 30 degrees.
What is an angle?When two lines or rays converge at the same point, the measurement between them is called a "Angle."
We have a diagram shown in the picture.
The measure of an angle is 30 degrees shown.
The triangle is a right-angled triangle
30-60-90
Two parallel lines are shown which are intersected by a transversal.
The adjacent angle is 60 degrees.
The measure of angle θ:
θ = 90 - 60
θ = 30 degrees
Thus, the measure of the angle θ is 30 degrees, or the magnitude of theta is 30 degrees.
Learn more about the angle here:
brainly.com/question/7116550
#SPJ1

e) (5p points) we are given the following unilateral z-transform, i.e. the system is causal ????(????) = ???? (???? − ????) ???? − ???? −???? (???? − ????) ???? − ???????? −???? ???? − ???? find y[n] the inverse z-transform of y(z) and list the values from n = 0 to 8
Answers
The values of n range from 0 to 8, so let's calculate y[n] for n = 0, 1, 2, ..., 8 using the inverse z-transform table.
To find the inverse z-transform of y(z), we can use the method of partial fraction decomposition. Let's break down the given unilateral z-transform equation:
Y(z) = X(z) * (z - a) / (z - b) * (z - c) / (z - d)
Here, a, b, c, and d represent the roots of the denominator polynomial.
To find y[n], we need to find the coefficients of the terms in the partial fraction decomposition.
Now, let's substitute z = e^(jw) into the equation:
Y(e^(jw)) = X(e^(jw)) * (e^(jw) - a) / (e^(jw) - b) * (e^(jw) - c) / (e^(jw) - d)
After simplification, we can express Y(e^(jw)) as a sum of terms:
Y(e^(jw)) = A / (1 - be^(-jw)) + B / (1 - ce^(-jw)) + C / (1 - de^(-jw))
Now, we can use the inverse z-transform table to find the corresponding time-domain sequence y[n] for each term.
The values of n range from 0 to 8, so let's calculate y[n] for n = 0, 1, 2, ..., 8 using the inverse z-transform table.
To know more about inverse z-transform visit:
brainly.com/question/24600056
#SPJ11
I am Desperate for answer

Answers
The mean is 8 and the lower quartile is 6.
what is the probability that a randomly selected student from this group is enrolled in a music or art course?
Answers
The probability that a randomly selected student from this group is enrolled in a music or art course is 0.7 or 70%.
The probability that a randomly selected student from this group is enrolled in a music or art course depends on the number of students enrolled in these courses and the total number of students in the group.
To calculate the probability, we need to determine the number of students enrolled in music or art courses and divide it by the total number of students in the group.
Let's assume we have the following information:
- Total number of students in the group: N
- Number of students enrolled in music course: M
- Number of students enrolled in art course: A
The probability that a randomly selected student is enrolled in a music or art course can be calculated as:
**P(Music or Art) = (M + A) / N**
For example, if there are 50 students in the group, with 20 students enrolled in music and 15 students enrolled in art, the probability would be:
P(Music or Art) = (20 + 15) / 50 = 35 / 50 = 0.7 or 70%
Therefore, the probability that a randomly selected student from this group is enrolled in a music or art course is 0.7 or 70%.
It is important to note that the accuracy of the probability calculation depends on the accuracy of the given information regarding the number of students enrolled in music and art courses, as well as the total number of students in the group.
Learn more about probability here
https://brainly.com/question/25839839
#SPJ11
Solve
9
-
)
12
OA)
0010
100
8
OB)
OC)
5
12
OD)
olu
5
12
Answers
Round o.oo9 to the nearest hundredth.
Answers
Answer:
0.01
Step-by-step explanation:
When rounding to the nearest hundredth, you look in the thousandths place to see if the number is 5 or greater. In this case it is. The hundredths place then moves up one number.
=0.01
Hope this helps!
A store pays $24 for a jewelry box and marks the price up by 20%. What is the amount of
the mark-up?
Answers
Answer:
$4.8
Step-by-step explanation:
$24×20/100=$4.8
Divide these polynomials. (8x³ + 2x² - 7x + 2) ÷ (2x - 1)
A. 4x² + 3x - 2
B. 4x² + 6x - 1
C. 4x² + 3x + 2
D. 4x² - 3x - 2
Answers
Answer:
The answer is letter A.
(8x³ + 2x² - 7x + 2) ÷ (2x - 1)
8x³ + 2x² - 7x + 2 ÷ 2x - 1
(2x-1)(4x²+3x-2)÷2x-1
cancel 2x-1 so that the answer is 4x²+3x-2.
Calculate the angle marked with a question mark. Do not measure - the drawing is not to scale

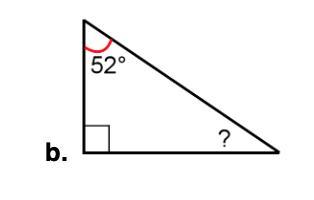
Answers
Answer:
crbtbynynumyvscwcsbymumybrxqzwcrhy
What is the greatest common factor in the expression 10x2 + 10x?
AO 10
B. 10x + 1
c. 10x
DOX
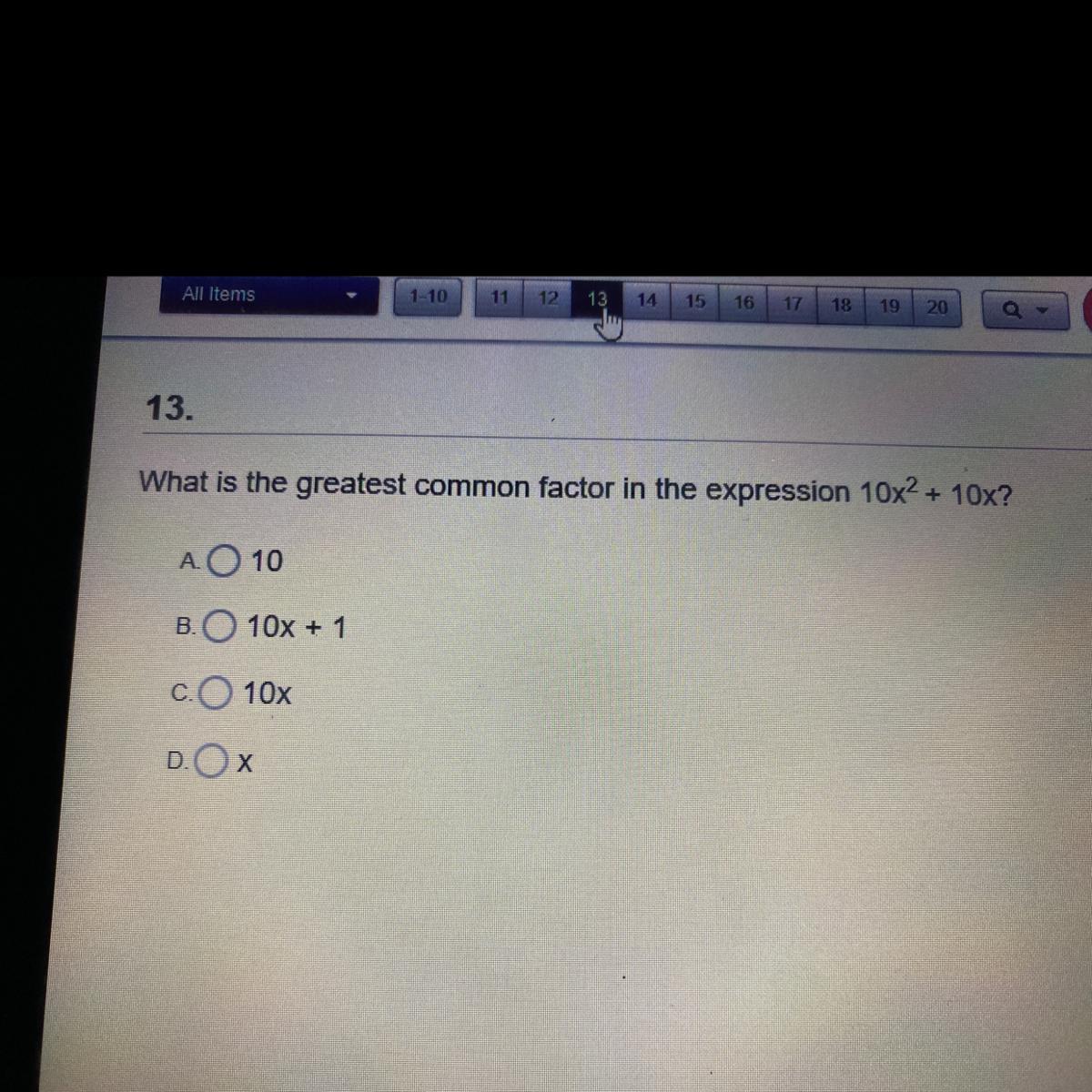
Answers
Answer:
10x C
Step-by-step explanation:
10x (10x+1)= 10x^2+10x
Price of Gasoline The average retail price of gasoline (all types) for the first half of 2005 was $212.2 cents. What would the standard deviation have to be in order for a 10% probability that a gallon of gas costs less than $1.80? Round -value calculations to two decimal places and final answer to the nearest cent.
Answers
Probability that a gallon of gasoline costs less than $1.80.To calculate the standard deviation for a 10% probability that a gallon of gasoline costs less than $1.80, we need to use the z-score formula. The z-score represents how many standard deviations away from the mean a specific value is. In this case, the mean price of gasoline is $2.122, and we want to find the standard deviation for the price of $1.80.
First, we need to find the z-score corresponding to a 10% probability. Using a standard normal distribution table, we find that a z-score of approximately -1.28 corresponds to a 10% probability.
Now, we can set up the z-score formula:
z = (X - μ) / σ
where z is the z-score, X is the specific value, μ is the mean, and σ is the standard deviation.
Plug in the values:
-1.28 = ($1.80 - $2.122) / σ
Solve for σ:
σ = ($1.80 - $2.122) / -1.28
σ ≈ 0.252
Rounding to the nearest cent, the standard deviation would have to be approximately $0.25 for a 10% probability that a gallon of gasoline costs less than $1.80.
learn more about Probability here: brainly.com/question/30034780
#SPJ11
which of the following is most likely to generalize to its population of interest? a random sample of 6 a stratified random sample of 120 a convenience sample of 12,000 a quota sample of 1,200
Answers
The most likely to generalize to it's population of interest is a stratified random sample of 120
a stratified random sample 120
Stratified random sampling is a method of sampling that involves the division of a population into smaller subgroups known as strata. In stratified random sampling, or stratification, the strata are formed based on members’ shared attributes or characteristics, such as income or educational attainment. Stratified random sampling has numerous applications and benefits, such as studying population demographics and life expectancy.
Stratified random sampling is also called proportional random sampling or quota random sampling.Stratified random sampling allows researchers to obtain a sample population that best represents the entire population being studied.Sampling involves statistical inference made using a subset of a population.Stratified random sampling is done by dividing the entire population into homogeneous groups called strata.Proportional stratified random sampling involves taking random samples from stratified groups, in proportion to the population. In disproportionate sampling, the strata are not proportional to the occurrence of the population.To learn more about stratified random sampling:
https://brainly.com/question/20692763
#SPJ4
please help will give brainliest

Answers
Find the velocity and acceleration vectors in terms of ur and up r = a(2 sin t) and 0= 1- e-t, where a is a constant V = u₁ + ue a = u₁ + ue
Answers
the velocity vector is v = a(-cos t)uᵣ + a(\(e^{-t\))uθ, and the acceleration vector is a = (sin t)uᵣ + (-\(e^{-t\))uθ.
To find the velocity and acceleration vectors in terms of unit vectors uᵣ and uθ for the given position vector r = a(2 - sin t) and θ = 1 - \(e^{-t\) we need to differentiate the position vector with respect to time.
Given that r = a(2 - sin t), we can find the velocity vector v by differentiating r with respect to time:
v = dr/dt
To differentiate r with respect to t, we differentiate each component separately. The component r in the radial direction is given by r = a(2 - sin t), and the component in the tangential direction is rθ = aθ.
Differentiating rᵣ with respect to t:
dr/dt = d(a(2 - sin t))/dt
= a(-cos t)
Differentiating rθ with respect to t:
drθ/dt = d(aθ)/dt
= a(d(1 - \(e^{-t\))/dt)
= a(\(e^{-t\))
Therefore, the velocity vector v can be written as:
v = (drᵣdt)uᵣ + (drθ/dt)uθ
= a(-cos t)uᵣ + a(\(e^{-t\))uθ
Next, to find the acceleration vector a, we differentiate the velocity vector v with respect to time:
a = dv/dt
Differentiating (-cos t)uᵣ with respect to t:
d((-cos t)uᵣ)/dt = (-d(cos t)/dt)uᵣ
= sin t uᵣ
Differentiating (\(e^{-t\))uθ with respect to t:
d((\(e^{-t\))uθ)/dt = (d(\(e^{-t\))/dt)uθ
= -\(e^{-t\)uθ
Therefore, the acceleration vector a can be written as:
a = (sin t)uᵣ + (-\(e^{-t\))uθ
Hence, the velocity vector is v = a(-cos t)uᵣ + a(\(e^{-t\))uθ, and the acceleration vector is a = (sin t)uᵣ + (-\(e^{-t\))uθ.
Learn more about Velocity here
https://brainly.com/question/32525933
#SPJ4
A state highway patrol official wishes to estimate the percentage/proportion of drivers that exceed the speed limit traveling a certain road.
A. How large a sample is needed in order to be 95% confident that the sample proportion will not differ from the true proportion by more than 3 %? Note that you have no previous estimate for p.
B. Repeat part (A) assuming previous studies found that the sample percentage of drivers on this road who exceeded the speed limit was 65%
Answers
A) Approx. 1067 is the required sample size to ensure 95% confidence that the sample proportion will not differ from the true proportion by more than 3%.
B) When the previous estimate is 65%, approx. 971 is the sample size needed to achieve 95% confidence that the sample proportion will not differ by more than 3% from the true proportion.
How to calculate the sample size needed for estimating the proportion?To determine the sample size needed for estimating the proportion of drivers exceeding the speed limit, we can use the formula for sample size calculation for proportions:
n = (Z² * p * (1 - p)) / E²
where:
n = the sample size.
Z = the Z-value associated with the confidence level of 95%.
p = the estimated proportion or previous estimate.
E = the maximum allowable error, which is 3% or 0.03.
We calculate as follows:
A. No previous estimate for p is available:
Here, we will assume p = 0.5 (maximum variance) since we don't have any prior information about the proportion. So, adding the values into the formula:
n = (Z² * p * (1 - p)) / E²
n = ((1.96)² * 0.5 * (1 - 0.5)) / 0.03²
n= (3.842 * 0.5 * (0.5))/0.03²
n = (1.9208*0.5)/0.0009
n ≈ 1067.11
Thus, to be 95% confident that the sample proportion will not differ from the true proportion by more than 3%, a sample size of approximately 1067 is required.
B. Supposing previous studies found that the sample percentage of drivers who exceeded the speed limit is 65%:
Here, we have a previous estimate of p = 0.65:
Putting the values into the formula:
n = (Z²* p * (1 - p)) / E²
n = ((1.96)² * 0.65 * (1 - 0.65)) / 0.03²
n= (3.842 * 0.65 *(0.35))/0.0009
n ≈ 971
Hence, with the previous estimate of 65%, a sample size of approximately 971 is necessary to be 95% confident that the sample proportion will not differ from the true proportion by more than 3%.
Learn more about sample size calculation at brainly.com/question/30647570
#SPJ4
A scuba cylinder that normally lasts one hour at the surface will last _______ minutes at 20 meters/66 feet
Answers
A scuba cylinder that normally lasts one hour at the surface will last 20 minutes at 66 feet.
According to the statement
We have given that the A scuba cylinder that normally lasts one hour at the surface. And we have to find that the for how much time the cylinder at the surface will last 66 feet.
So, For this purpose, we know that the
A Scuba cylinder or diving gas cylinder is a gas cylinder used to store and transport high pressure gas used in diving operations.
So, we have given that the
Scuba cylinder that normally lasts one hour.
So, according to this information the cylinder lasts for 20 minutes at the surface of 66 feet.
So, A scuba cylinder that normally lasts one hour at the surface will last 20 minutes at 66 feet.
Learn more about Scuba cylinder here
https://brainly.com/question/23935577
#SPJ4
Could someone please answer these 2

Answers
Answer:
A. 1/6
B. 1
Step-by-step explanation:
A. 9/j x j/54= 9/54 = 1/6
B. 6k/8m : 3k/4m = 6k/8m : 4m / 3k = 2/2 =1
Answer:
a. 3/2
b. 1
Step-by-step explanation:
A. To simplify the expression, we can cancel out the common factor of j:
9/j * j/54 = (9/1 * 1/6) = 3/2
Therefore, 9/j * j/54 simplifies to 3/2.
B. To divide fractions, we can multiply the first fraction by the reciprocal of the second fraction. That is,
(a/b) ÷ (c/d) = (a/b) x (d/c)
Using this rule, we can simplify the given expression as follows:
6k/8m ÷ 3k/4m = (6k/8m) x (4m/3k)
= (6/8) x (4/3)
= 2/2
= 1
A researcher collects two samples of data. He finds the first sample (n=8) has a mean of 5 ; the second sample (n=2) has a mean of 10 . What is the weighted mean of these samples?
Answers
The weighted mean of the two samples is 6, suggesting that the average value is calculated by considering the weights assigned to each sample, resulting in a mean value of 6 based on the given weighting scheme.
To calculate the weighted mean of two samples, we need to consider the sample sizes (n) and the mean values. The weighted mean gives more importance or weight to larger sample sizes. In this case, we have two samples, one with n=8 and the other with n=2.
The formula for the weighted mean is:
Weighted Mean = (n₁ * mean₁ + n₂ * mean₂) / (n₁ + n₂)
where:
n₁ = sample size of the first sample
mean₁ = mean of the first sample
n₂ = sample size of the second sample
mean₂ = mean of the second sample
Substituting the given values:
n₁ = 8
mean₁ = 5
n₂ = 2
mean₂ = 10
Weighted Mean = (8 * 5 + 2 * 10) / (8 + 2)
= (40 + 20) / 10
= 60 / 10
= 6
Therefore, the weighted mean of the two samples is 6.
The weighted mean provides a measure of the average that takes into account the relative sizes of the samples. In this case, since the first sample has a larger sample size (n=8) compared to the second sample (n=2), the weighted mean is closer to the mean of the first sample (5) rather than the mean of the second sample (10). This is because the larger sample size has a greater influence on the overall average.
For more such questions on mean visit:
https://brainly.com/question/1136789
#SPJ8
Please help me (this is one questionn)


Answers
Answer:
Below.
Step-by-step explanation:
Reading off the graph:
y-intercept = (0, 2.5)
x-intercept = (3.5, 0)
what transformation is represented by the rule (x, y)→(x−1, y+3) ?
Answers
Answer:
the reflection across the x-axis rotation of 180° about the origin reflection across the y-axis rotation of 90° clockwise about the origin.
Step-by-step explanation:
hope this help ;]
What is the image of ( -7,5) after a reflection over the line y = -x?
Answers
Answer:
(-5, 7)
Step-by-step explanation:
(x,y) over y= -x = (-y, -x)
(-7, 5) is turned to (-5, 7)
1. (100 points) Consider a utility function given by
u(ct)=ln(ct)+βln(ct+1) where β=1/1+rho
and the constraints are given by yt=ct+st
yt+1+(1+r)st=ct+1
(a) (10 points) Combine the two constraints by eliminating st
(b) (10 points) Solve the constraint for ct+1
(c) (10 points) Plug the constraint into ct+1 in the utility function.
(d) (20 points) Differentiate the utility function with respect to ct
(e) (20 points) Derive the Euler Equation.
(f) (20 points) What is the intuitive interpretation of the Euler Equation?
(g) (10 points) Suppose rho=0.05 and the real interest rate is 3%. Which is larger; ct ct+1? Why?
Answers
(a) The value of st from the second constraint into the first constraint is yt = ct + (ct+1 - ct) = 2ct + ct+1, (b) The constraint for ct+1 is yt - 2ct, (c) u(ct) = ln(ct) + βln(yt - 2ct), (d) u'(ct) = 1/ct - 2β/(yt - 2ct), (e) 1/ct = 2β/(yt - 2ct), (f) The intuitive interpretation of the Euler Equation is that it represents the optimal intertemporal consumption choice, (g) β = 0.9524.
(a) To combine the two constraints, we can substitute the value of st from the second constraint into the first constraint:
yt = ct + st
yt = ct + (ct+1 - ct) = 2ct + ct+1
(b) Solving the constraint for ct+1, we get:
yt = 2ct + ct+1
ct+1 = yt - 2ct
(c) Plugging the constraint into ct+1 in the utility function, we have:
u(ct) = ln(ct) + βln(yt - 2ct)
(d) Differentiating the utility function with respect to ct, we get:
u'(ct) = 1/ct - 2β/(yt - 2ct)
(e) To derive the Euler Equation, we set the derivative of the utility function with respect to ct equal to 0:
0 = 1/ct - 2β/(yt - 2ct)
Simplifying, we have:
1/ct = 2β/(yt - 2ct)
(f) The intuitive interpretation of the Euler Equation is that it represents the optimal intertemporal consumption choice. It states that the marginal benefit of consuming one additional unit today (1/ct) is equal to the discounted marginal benefit of consuming one additional unit tomorrow (2β/(yt - 2ct)).
(g) If rho=0.05 and the real interest rate is 3%, we can calculate the value of β:
β = 1/(1+rho)
= 1/(1+0.05)
= 0.9524
To determine whether ct or ct+1 is larger, we need more information.
To know more about intertemporal visit:
https://brainly.com/question/32540714
#SPJ11
Please hep me solve picture below thank uou

Answers
Answer:
x= -1, -13
Step-by-step explanation:

Answer: x=-13 x=-1
Step-by-step explanation:
\(x^2+14x=-13\\x^2+2(x)(7)+7^2-7^2=-13\\(x^2+2(x)(7)+7^2)-49=-13\\(x+7)^2-49=-13\\(x+7)^2-49+49=-13+49\\(x+7)^2=36\)
\((x+7)^2-36=36-36\\(x+7)^2-36=0\\(x+7)^2-6^2=0\\(x+7+6)(x+7-6)=0\\(x+13)(x+1)=0\\x+13=0\\x+13-13=0-13\\x=-13\\x+1=0\\x+1-1=0+(-1)\\x=-1\)
Help 14x^2 + 10 - 3x^2- 3
a) 11x^2 + 2x + 7 ,b) 11x^2 + 10 ,c) 11x^2 + 13 ,d) 11x^2 + 7
Answers
Answer:
D) 11x² + 7
Step-by-step explanation:
combine "like" terms
let be a random variable with pdf f(x)=12/X^3, x>=a where is a constant . find the value of the constant a (round off to second decimal place).
Answers
The random variable can only take on values greater than or equal to 2.83
A random variable is a variable that can take on different values depending on the outcome of a random process.
In this problem, we are given a probability density function (pdf) for a random variable and asked to find the value of the constant "a". The pdf, f(x), represents the probability of the random variable taking on a particular value, x.
Here we have the constant "a" in the equation
=> f(x)=12/X³, x>=a,
is the minimum value that the random variable can take on.
This means that the total probability of the random variable taking on any value between "a" and infinity must equal 1.
Now by using calculus, we can find the value of "a" by solving the equation
=> ∫(a,∞) (12/X³) = 1.
This equation tells us that the total probability of the random variable taking on any value greater than "a" must equal 1.
By solving for "a", we find that it is approximately equal to 2.83.
To knw more about probability here.
https://brainly.com/question/11234923
#SPJ4
a) Factor f(x)=−4x^4+26x^3−50x^2+16x+24 fully. Include a full solution - include details similar to the sample solution above. (Include all of your attempts in finding a factor.) b) Determine all real solutions to the following polynomial equations: x^3+2x^2−5x−6=0 0=5x^3−17x^2+21x−6
Answers
By using factoring by grouping or synthetic division, we find that \(x = -2\) is a real solution.
Find all real solutions to the polynomial equations \(x³+2x ²-5x-6=0\) and \(5x³-17x²+21x-6=0\).Checking for Rational Roots
Using the rational root theorem, the possible rational roots of the polynomial are given by the factors of the constant term (24) divided by the factors of the leading coefficient (-4).
The possible rational roots are ±1, ±2, ±3, ±4, ±6, ±8, ±12, ±24.
By substituting these values into \(f(x)\), we find that \(f(-2) = 0\). Hence, \(x + 2\) is a factor of \(f(x)\).
Dividing \(f(x)\) by \(x + 2\) using long division or synthetic division, we get:
-4x⁴ + 26x³ - 50x² + 16x + 24 = (x + 2)(-4x³ + 18x² - 16x + 12)Now, we have reduced the problem to factoring \(-4x³ + 18x² - 16x + 12\).
Attempt 2: Factoring by Grouping
Rearranging the terms, we have:
-4x³ + 18x² - 16x + 12 = (-4x^3 + 18x²) + (-16x + 12) = 2x²(-2x + 9) - 4(-4x + 3)Factoring out common factors, we obtain:
-4x³+ 18x² - 16x + 12 = 2x²(-2x + 9) - 4(-4x + 3) = 2x²(-2x + 9) - 4(3 - 4x) = 2x²(-2x + 9) + 4(4x - 3)Now, we have \(2x^2(-2x + 9) + 4(4x - 3)\). We can further factor this as:
2x²(-2x + 9) + 4(4x - 3) = 2x² (-2x + 9) + 4(4x - 3) = 2x²(-2x + 9) + 4(4x - 3) = 2x²(-2x + 9) + 4(4x - 3) = (2x² + 4)(-2x + 9)Therefore, the fully factored form of \(f(x) = -4x⁴ + 26x³ - 50x² + 16x + 24\) is \(f(x) = (x + 2)(2x² + 4)(-2x + 9)\).
Solutions to the polynomial equations:
\(x³ ³ + 2x² - 5x - 6 = 0\)Using polynomial division or synthetic division, we can find the quadratic equation \((x + 2)(x² + 2x - 3)\). Factoring the quadratic equation, we get \(x² + 2x - 3 = (x +
Learn more about synthetic division
brainly.com/question/28824872
#SPJ11