За
(A)
2a 11
==+a (5 marks to solve; 2 marks to verify)
3 6
4
Answers
Answer:
jonwjwjejejeken 20 ow91
Related Questions
What is the value of the power a if 5^a = 1/125
Answers
Answer:
a = -3
Step-by-step explanation:
5^a = 1/125
The fraction 1/125 can be written as a power with base 5.
5^a = 5^(-3)
Cancel the same bases on both sides.
a = -3
Answer:
a = -3.
Step-by-step explanation:
5^a = 1/125
1/125 = 1 / 5^3
= 5^-3
5^a = 5^-3
so a = -3.
A radioactive substance has an initial mass of 475 grams and a half-life of 20 days. What equation is used to determine the number of days, x, required for the substance to decay to 63 grams?
Answers
The equation used to determine the number of days, x, required for the substance to decay to 63 grams is: x ≈ 83.60
To determine the number of days, x, required for a radioactive substance to decay to 63 grams, we can use the exponential decay formula. The equation that represents the decay of a radioactive substance over time is:
N(t) = N₀ * (1/2)^(t/h)
Where:
N(t) is the remaining mass of the substance at time t
N₀ is the initial mass of the substance
t is the time elapsed
h is the half-life of the substance
In this case, we have an initial mass of 475 grams, and we want to find the number of days required for the substance to decay to 63 grams. We can set up the equation as follows:
63 = 475 * (1/2)^(x/20)
To solve for x, we can isolate the exponential term on one side of the equation:
(1/2)^(x/20) = 63/475
Next, we can take the logarithm (base 1/2) of both sides to eliminate the exponential term:
log(base 1/2) [(1/2)^(x/20)] = log(base 1/2) (63/475)
By applying the logarithmic property log(base b) (b^x) = x, the equation simplifies to:
x/20 = log(base 1/2) (63/475)
Finally, we can solve for x by multiplying both sides of the equation by 20:
x = 20 * log(base 1/2) (63/475)
Using a calculator to evaluate log(base 1/2) (63/475) ≈ 4.1802, we find:
x ≈ 20 * 4.1802
x ≈ 83.60
For more such questions on equation visit:
https://brainly.com/question/22688504
#SPJ8
The number of people who have entered a museum on a certain day is modeled by a function f(t), where t is measured in hours since the museum opened that day. The number of people who have left the museum since it opened that same day is modeled by a function, g(t). If f'(t) = 380(1.02^t) and g'(t) = 240 + 240 sin (π(t-4)/12) at what time t for 1 ≤ t ≤ 11, is the number of people in the (12) museum at a maximum? (A) 1 (B) 7.888 (C) 9.446 (D) 10.974 (E) 11
Answers
Bisection method is a numerical method used to find the root of a function by repeatedly bisecting an interval and determining which subinterval the root lies in, until the root is found.
To find the time at which the number of people in the museum is at a maximum, we need to find when the rate at which people are entering the museum (f'(t)) is equal to the rate at which people are leaving the museum (g'(t)).
Setting f'(t) = g'(t), we get:
380(1.02^t) = 240 + 240 sin (π(t-4)/12)
Simplifying, we get:
1.58(1.02^t) = 1 + sin(π(t-4)/12)
We can use a graphing calculator or numerical methods to solve for t.
Using a graphing calculator, we can graph the functions y = 1.58(1.02^x) and y = 1 + sin(π(x-4)/12) and find the point of intersection on the interval 1 ≤ x ≤ 11.
Alternatively, we can use numerical methods such as the bisection method or Newton's method to approximate the solution.
Using either method, we find that the solution is t ≈ 9.446.
Therefore, the answer is (C) 9.446.
To know more about bisection method visit:
https://brainly.com/question/28836241
#SPJ11
Select the expression that is equivalent to x + x + y × y × y. Question 11 options: (a)x^2 + 3y (b)2x + 3y (c)x^2 + y^3 (d)2x + y^3
Answers
x+x+y.y.y = 2x+y^3 ( y cube)
So, The answer is (d)
1
What is the value of 3 divided by
2
Answers
Answer:
1.5
Step-by-step explanation:
Answer:
1.5
Step-by-step explanation:
its pretty simple- 1 + 1 = 2 .5 + .5 = 1 2 + 1 = 3
What is 792 divided by 44
Answers
792/44 = 18
pls help w work and explanation fast thanks
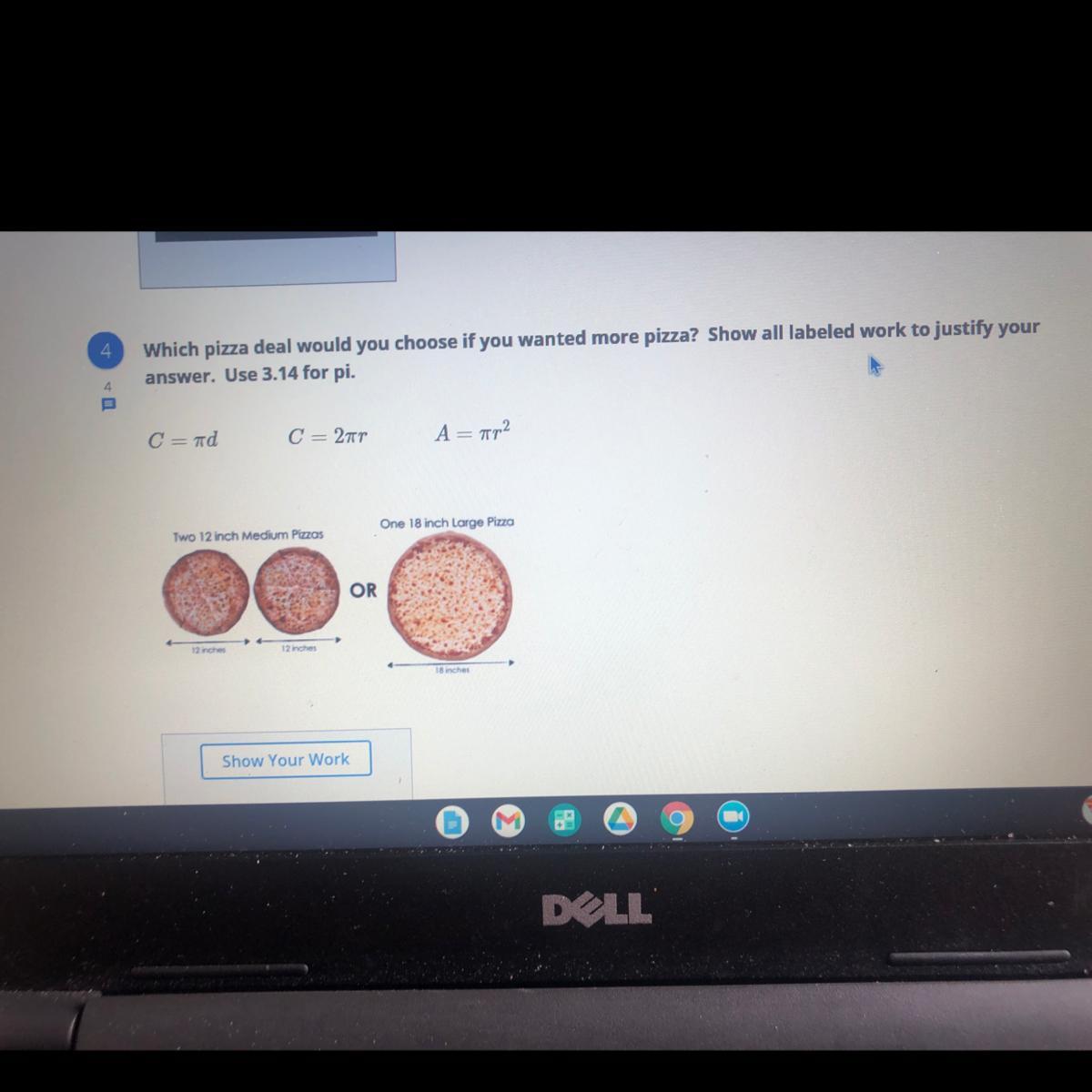
Answers
Answer:
I would choose two 12 inch pizza if I want more pizza as two 12 inch pizzas have larger circumference than one 18 inch pizza
c=πd
circumference= pie × diameter
c=2πr
circumference= 2×pie×radius
A=πr²
Area= pie×square radius
Pie= 22/7, 3.14( depends on the question, sometimes the value of pie will be given in the question)
radius= half of diameter
To find perimeter of circle use 2πr
To find area of circle use πr² or πd


Create a rational expression that simplifies to 2x/(x+1)
and that has the following restrictions on x:
x ≠ −1, 0, 2, 3. Write your expression here.
Answers
Answer:
One possible rational expression that simplifies to 2x/(x+1) and meets the given restrictions is:
(4x^2 - 2x - 3) / [(x + 1)(x - 3)(x - 2)]
To see why this expression simplifies to 2x/(x+1), we can simplify the numerator and denominator separately:
Numerator:
2x(2x-1) = 4x^2 - 2x
Denominator:
(x+1)(x-3)(x-2)
Multiplying the numerator and denominator by -1 gives:
(-2x)(2x-1) / [(3-x)(2-x)(1+x)]
Then, we can rearrange the factors in the denominator to get:
(-2x)(2x-1) / [(x+1)(x-2)(x-3)]
Now we have the desired rational expression that simplifies to 2x/(x+1) and has the given restrictions on x.
Step-by-step explanation:
3. The carrying capacity of a drain pipe is directly proportional to the area of its cross- section. If a cylindrical drain pipe can carry 36 litres per second, determine the percentage increase in the diameter of the drain pipe necessary to enable it to carry 60 litres per second.
Answers
The percentage increase in the diameter of the drain pipe necessary to enable it to carry 60 litres per second is 28.87%.
Given that the carrying capacity is directly proportional to the area, we can write:
C1 ∝ A1 = πr₁²
Since the carrying capacity is directly proportional to the area, we have:
C2 ∝ A2 = πr₂²
To find the percentage increase in diameter, we need to find the ratio of the increased area to the initial area and then express it as a percentage. Let's calculate this ratio:
(A2 - A1) / A1 = (πr₂² - πr₁²) / (πr₁²) = (r₂² - r₁²) / r₁²
We can also express the ratio of the increased carrying capacity to the initial carrying capacity:
(C2 - C1) / C1 = (60 - 36) / 36 = 24 / 36 = 2 / 3
Since the area and the carrying capacity are directly proportional, the ratios should be equal:
(r₂² - r₁²) / r₁² = 2 / 3
Now, let's substitute r = D/2 in the equation:
((D₂/2)² - (D₁/2)²) / (D₁/2)² = 2 / 3
(D₂² - D₁²) / D₁² = 2 / 3
Cross-multiplying:
3(D₂² - D₁²) = 2D₁²
3D₂² - 3D₁² = 2D₁²
3D₂² = 5D₁²
Dividing by D₁²:
3(D₂² / D₁²) = 5
(D₂² / D₁²) = 5 / 3
Taking the square root of both sides:
D₂ / D₁ = √(5/3)
To find the percentage increase in diameter, we subtract 1 from the ratio and express it as a percentage:
Percentage increase = (D₂ / D₁ - 1) × 100
Percentage increase = (√(5/3) - 1) × 100
Percentage increase = 28.87%
To learn more on Percentage click:
https://brainly.com/question/24159063
#SPJ1
Which represents the polynomial written in standard form?
8x2y2 – StartFraction 3 x cubed y Over 2 EndFraction + 4x4 – 7xy3
Answers
Answer:
Step-by-step explanation:

Answer:
A
Step-by-step explanation:
Parking at a large university has become a very big problem. University administrators are interested in determining the average parking time (e.g. the time it takes a student to find a parking spot) of its students. An administrator inconspicuously followed 300 students and carefully recorded their parking times. Identify the population of interest to the university administration.
a. The 250 students that data was collected from.
b. The entire set of students that park at the university.
c. The entire set of students, faculty and staff that park at the university.
d. The students that park between 9 and 10 A.M on wednesday.
Answers
Answer:
D
Step-by-step explanation:
Answer:
b. The entire set of students that park at the university.
Step-by-step explanation:
Since the University is interested in determining the average parking time of its students, the population of interest is the entire set of students that park at the university.
The correct option is B.
Note that the 300 students whose parking time was recorded forms a sample of the population under study.
Find the slope of the line graphed below. PLEASE HELP ME

Answers
Answer:
-3/5
Step-by-step explanation:
I was always taught rise over run. count how many units up/down the next point is and how many units over.
P = 149t +15900
gives the total population, P, of a small city, t, years after 1993. Use the equation to determine when (what year) the population reached a population of 17837 people
Answers
Answer:
In 2006 the population will reach 17837
Step-by-step explanation:
P in the given t = 17837
P is also given as;
P = 149t +15900
17837=149t +15900 ( by putting the value of P from given questions)
17837-15900=149t
1937=149t
then,
T=1937/149
=13
Now,
T = 13 years
the given year is 1993
soo, 1993+13
=2006
what is 4/5-1/6 with work shown
Answers
the denominators need to be the same so if we multiply the first fraction by 6 and the second by 5, our new equation is
24/30 - 5/30
24-5=19
19/30 is your answer
Answer & Step-by-step explanation:
\(\frac{4}{5}-\frac{1}{6}\)
When you need to subtract fractions, the denominators (bottom) need to be the same. For this, you have to multiply both fractions until the bottom numbers are the same:
Find the lowest common multiple of the denominators:
\(5,10,15,20,25,30\\6,12,18,24,30\)
The LCM of 5 and 6 is 30. Now you have to multiply the top and bottom of the fractions until you get a denominator of 30*:
\(\frac{4(6)}{5(6)}=\frac{24}{30}\\\\\frac{1(5)}{6(5)}=\frac{5}{30}\)
So,
\(\frac{24}{30} -\frac{5}{30}\)
When you subtract fractions, you only change the numerators (top). The denominator will stay the same:
\(\frac{24}{30} -\frac{5}{30}=\frac{19}{30}\)
Since the fraction can't be further simplified, \(\frac{4}{5}-\frac{1}{6}=\frac{19}{30}\)
:Done
*When you are finding the same denominators, you need to multiply a single fraction's numerator and denominator by the same number. The two different fractions don't need to be multiplied by the same number:
\(\frac{x(a)}{y(a)}-\frac{w(b)}{z(b)}\)
the measure of one angle of an isosceles trapezoid is x and the angle opposite it is x+20,what is the value of x
Answers
Answer:
X=80
Step-by-step explanation:
I suppose the graph will be like this:
Since isosceles trapezoid, red lines are parallel.
X+x+20= 180
2x+20=180
2x=160
X=80

What is the quotient?
212÷(−134)
Enter your answer as a mixed number, in simplified form, in the box.
Answers
The quotient of 212÷(−134) will be -1 39/67.
What is a quotient?A quotient in mathematics is the amount created by dividing two numbers. In mathematics, the term "quotient" is frequently used to refer to the integer portion of a division, as well as to a fraction or a ratio.
When dividing a number, a remnant is produced if the division is not exact. Let's use an illustration to better grasp this. Divide the dividend by the divisor to determine the quotient. Dividend times Divisor is the quotient.
In this case, quotient will be -1 39/67. This simply means the division of the numbers.
Learn more about quotient on:
https://brainly.com/question/11418015
#SPJ1
Describe the main parts of a proof.
Answers
Answer:
The most common form of explicit proof in high school geometry is two column proof consists of various five parts they are; the given, the proposition, the statement column, the reason column, and the diagram ( if its given).
Answer:
Proofs contain given information and a statement to be proven. You use deductive reasoning to create an argument with justification of steps using theorems, postulates, and definitions. Then you arrive at a conclusion.
Step-by-step explanation:
-9(14d - 13e) =
*As an expression*
Answers
Answer:
Solution given:-9(14d - 13e) =117e-126d is your answer
Yasmine earns $11.75 per hour and works 35 hours per week. She has a young child and feel like she cannot spend more than 30% of her total income on rent. What is the maximum monthly rent that she should pay? Assume that she gets paid 4 times in one month. Round your answer to two decimal places.
Answers
The maximum monthly rent that Yasmine should pay is approximately $619.58.
To calculate the maximum monthly rent that Yasmine should pay, we need to determine her monthly income and then find 30% of that amount.
Yasmine's hourly = $11.75
Hours worked per week = 35
Weekly income = Hourly wage * Hours worked per week
= $11.75 * 35
= $411.25
Monthly income = Weekly income * Number of weeks in a month
= $411.25 * 4
= $1645
Now, let's calculate 30% of her monthly income:
Rent limit = 30% of Monthly income
= 0.30 * $1645
= $493.50
Therefore, the maximum monthly rent that Yasmine should pay is
To determine the maximum monthly rent that Yasmine can afford, we first calculate her monthly income. Since she earns $11.75 per hour and works 35 hours per week, we multiply her hourly wage by the number of hours worked per week to find her weekly income.
Next, we multiply her weekly income by the number of weeks in a month (which we assume to be 4) to obtain her monthly income.
Finally, we calculate 30% of her monthly income by multiplying it by 0.30, which represents 30% as a decimal.
The result, rounded to two decimal places, is the maximum monthly rent that Yasmine should pay. In this case, the maximum monthly rent is $493.50.
To know more about income, refer here:
https://brainly.com/question/2386757#
#SPJ11
If m
15 points thanks you :)


Answers
Answer:
48
Step-by-step explanation:
check the attached file

A triangle has area 100 square inches. It's dilated by a factor of k = 0.25.

Answers
1) The statement of Lin is correct.
2) (a) When scale factor, k = 9, area of the new triangle = 8100 square inches
(b) When k = 3/4, area of the new triangle = 56.25 square inches.
Given that,
A triangle has area 100 square inches.
It's dilated by a factor of k = 0.25.
When the triangle is dilated by a scale factor of k, then, each of the base and height is dilated by the scale factor of k.
So new area of the triangle after the dilation with the original triangle having base = b and height = h is,
Area of new triangle = 1/2 (kb)(kh) = k² (1/2 bh) = k² × Area of original triangle
Here original area = 100 square inches.
k = 0.25
New area = (0.25)² 100 = 6.25 square inches
So the correct statement is that of Lin.
Mai may found the new area by just multiplying the scale factor with 100, instead of taking the square of the scale factor. That is why she got 25 square inches as the new area.
2) (a) When k = 9,
Area of the new triangle = 9² (100) = 8100 square inches
(b) When k = 3/4
Area of the new triangle = (3/4)² (100) = 56.25 square inches
Hence the areas are found.
Learn more about Scale Factor here :
https://brainly.com/question/29464385
#SPJ1
The product of two numbers is 5430. If one of the numbers is 15 what is the other
number?
43
Answers
Answer:
362
Step-by-step explanation:
15xy=5430...therefore 5430divided by 15 is 362...so 362x15 their product is 5430
Please answer its fill in the blanks
the words are at the bottom

Answers
Answer:
1. Grassland
2. grass
3. Temperate grassland
4. prairies
5. steppe
6. tropical grassland
7. savanna
8. intermountain grassland
9. mixed prairie
10. tallgrass prairie
Step-by-step explanation:
Lily cuts 9 metres of wrapping paper into three pieces. The length of the first piece is 4.56 metres. The length of the second piece is 3.09 metres. Work out the length of the third piece.
Answers
Answer:
1.35 m
Step-by-step explanation:
Subtract the lengths of the 1st and 2nd pieces from the uncut piece:
9 - 4.56 - 3.09 = 1.35 m
Using the following weights:.3, 2, .5 find the forecast for the next period. Month 1 – 381, Month 2-366, Month 3 - 348. O a. 143 O b. 241 O c. 360 O d. 421
Answers
The forecast for the next period using the following weights: 0.3, 2, 0.5 is Option d. 421.
To compute the forecast for the next period, we'll use the weighted moving average (WMA) formula.WMA formula:
WMA = W1Yt-1 + W2Yt-2 + ... + WnYt-n
Where, WMA is the weighted moving average
W1, W2, ..., Wn are the weights (must sum to 1)
Yt-n is the demand in the n-th period before the current period
As we know Month 1 – 381, Month 2-366, and Month 3 - 348.
Weights: 0.3, 2, 0.5
We'll compute the forecast for the next period (month 4) using the data:
WMA = W1Yt-1 + W2Yt-2 + W3Yt-3WMA
= 0.3(381) + 2(366) + 0.5(348)WMA
= 114.3 + 732 + 174WMA
= 1020.3
Therefore, the forecast for the next period is 1020.3, which rounds to 421. Hence, option d is correct.
You can learn more about forecasts at: brainly.com/question/30167588
#SPJ11
Rose picked 18 tulips and 20 daffodils. She divided the flowers into groups so that the same number of tulips and daffodils were in each bouquet. What is the greatest number of bouquets she could have made?
Answers
Answer:
The greatest number of bouquets Rose could have is 2. 9 of each flower in each bouquet.
Step-by-step explanation:
Answer:
That depends on how many flowers we keep in each bouquet.
If 1 tulip & 1 daffodil is kept in a bouquet , then the greatest no. of bouquets she'll make = 18
If 2 tulips & 2 daffodils is kept in a bouquet , then the greatest no. of bouquets she'll make = 9
If 3 tulips & 3 daffodils is kept in a bouquet , then the greatest no. of bouquets she'll make = 6
If 6 tulips & 6 daffodils is kept in a bouquet , then the greatest no. of bouquets she'll make = 3
If 18 tulips & 18 daffodils is kept in a bouquet , then the greatest no. of bouquets she'll make = 2
but somehow 2 daffodils will be left .
A company's profit increased linearly from $5 million at the end of year 2 to $17 million at the end of year 6.
(a) Use the two (year, profit) data points (2, 5) and (6, 17) to find the linear relationship y = mx + b between x = year and y = profit.
(b) Find the company's profit at the end of 3 years.
(c) Predict the company's profit at the end of 8 years.
Answers
Below, you will learn how to solve the problem.
(a) To find the linear relationship y = mx + b between x = year and y = profit, we first need to find the slope (m) and the y-intercept (b).
The slope (m) is the change in y (profit) divided by the change in x (year):
m = (17 - 5)/(6 - 2)
m = 12/4
m = 3
Next, we can use one of the data points (2, 5) and the slope (3) to find the y-intercept (b):
5 = 3(2) + b
b = 5 - 6
b = -1
So the linear relationship between x = year and y = profit is:
y = 3x - 1
(b) To find the company's profit at the end of 3 years, we can plug in x = 3 into the equation:
y = 3(3) - 1
y = 8
So the company's profit at the end of 3 years is $8 million.
(c) To predict the company's profit at the end of 8 years, we can plug in x = 8 into the equation:
y = 3(8) - 1 = 23
So the company's profit at the end of 8 years is predicted to be $23 million.
For more information about equation, visit:
https://brainly.com/question/22688504
#SPJ11
Use Euler's method with step size \( h=0.1 \) to approximate the value of \( y(4.2) \) where \( y(x) \) is the solution to the following initial value problem. \[ y^{\prime}=7 x+8 y+3, \quad y(4)=2 \]
Answers
According to the question using Euler's method with a step size of \(\(h = 0.1\)\), the approximate value of \(\(y(4.2)\) is \(4.725\).\)
To approximate the value of \(\(y(4.2)\)\) using Euler's method with a step size of \(\(h = 0.1\),\) we can iterate through a series of steps to approximate the solution to the given initial value problem.
The general formula for Euler's method is:
\(\[y_{n+1} = y_n + h \cdot f(x_n, y_n)\]\)
where \(\(y_n\)\) represents the approximation of \(\(y\)\) at the \(\(n\)th\) step, \(\(x_n\)\) represents the \(\(x\)\) value at the \(\(n\)th\) step, \(\(h\)\) is the step size, and \(\(f(x_n, y_n)\)\) is the derivative of \(\(y\)\) with respect to \(\(x\)\) evaluated at \(\(f(x_n, y_n)\)
In this case, the initial value problem is:
\(\[\frac{{dy}}{{dx}} = 7x + 8y + 3, \quad y(4) = 2\]\)
We want to approximate \(\(y(4.2)\)\) using Euler's method with a step size of \(\(h = 0.1\).\)
Let's perform the iterations:
Step 1: Initialize the values
\(\[x_0 = 4, \quad y_0 = 2\]\)
Step 2: Perform the iterations
For \(\(n = 0\):\)
\(\[x_1 = x_0 + h = 4 + 0.1 = 4.1\]\)
\(\[y_1 = y_0 + h \cdot f(x_0, y_0) = 2 + 0.1 \cdot (7x_0 + 8y_0 + 3) = 2 + 0.1 \cdot (7 \cdot 4 + 8 \cdot 2 + 3) = 3.8\]\)
For \(\(n = 1\):\)
\(\[x_2 = x_1 + h = 4.1 + 0.1 = 4.2\]\)
\(\[y_2 = y_1 + h \cdot f(x_1, y_1) = 3.8 + 0.1 \cdot (7x_1 + 8y_1 + 3) = 3.8 + 0.1 \cdot (7 \cdot 4.1 + 8 \cdot 3.8 + 3) = 4.725\]\)
Step 3: Continue the iterations until reaching the desired value of \(\(x\)\), in this case, \(\(x = 4.2\).\)
Since we are approximating \(\(y(4.2)\)\), the final result of the iterations is\(\(y_2 = 4.725\).\)
Therefore, using Euler's method with a step size of \(\(h = 0.1\)\), the approximate value of \(\(y(4.2)\) is \(4.725\).\)
To know more about derivative visit-
brainly.com/question/32696592
#SPJ11
Question 7 of 10
For which sample size (n) and sample proportion (6) can a normal curve be
used to approximate the sampling distribution?
O A. n = 45; Ø = 0.8
O B. n = 90; 0 = 0.9
O C. n = 90; i = 0.8
D. n = 45; P = 0.9
SUBMIT

Answers
Answer:
C. n = 90; p = 0.8
Step-by-step explanation:
According to the Central Limit Theorem, the distribution of the sample means will be approximately normally distributed when the sample size, 'n', is equal to or larger than 30, and the shape of sample distribution of sample proportions with a population proportion, 'p' is normal IF n·p ≥ 10 and n·(1 - p) ≥ 10
Analyzing the given options, we have;
A. n = 45, p = 0.8
∴ n·p = 45 × 0.8 = 36 > 10
n·(1 - p) = 45 × (1 - 0.8) = 9 < 10
Given that for n = 45, p = 0.8, n·(1 - p) = 9 < 10, a normal distribution can not be used to approximate the sampling distribution
B. n = 90, p = 0.9
∴ n·p = 90 × 0.9 = 81 > 10
n·(1 - p) = 90 × (1 - 0.9) = 9 < 10
Given that for n = 90, p = 0.9, n·(1 - p) = 9 < 10, a normal distribution can not be used to approximate the sampling distribution
C. n = 90, p = 0.8
∴ n·p = 90 × 0.8 = 72 > 10
n·(1 - p) = 90 × (1 - 0.8) = 18 > 10
Given that for n = 90, p = 0.9, n·(1 - p) = 18 > 10, a normal distribution can be used to approximate the sampling distribution
D. n = 45, p = 0.9
∴ n·p = 45 × 0.9 = 40.5 > 10
n·(1 - p) = 45 × (1 - 0.9) = 4.5 < 10
Given that for n = 45, p = 0.9, n·(1 - p) = 4.5 < 10, a normal distribution can not be used to approximate the sampling distribution
A sampling distribution Normal Curve
45 × (1 - 0.8) = 9
90 × (1 - 0.9) = 9
90 × (1 - 0.8) = 18
45 × (1 - 0.9) = 4.5
Now we will investigate the shape of the sampling distribution of sample means. When we were discussing the sampling distribution of sample proportions, we said that this distribution is approximately normal if np ≥ 10 and n(1 – p) ≥ 10. In other words
Therefore;
A normal curve can be used to approximate the sampling distribution of only option C. n = 90; p = 0.8
(Please help me with this one it is due in ten minutes :'(
A snail is trying to get to the other side of a park. At what rate is the snail moving?
A) 1/2 foot per minute
B) 1 foot per minute
C) 1 1/2 feet per minute
D) 2 feet per minute

Answers
Answer:
I think the answer is C
Step-by-step explanation:
First you need to find 2 coordinates on the graph. (2,3) (4,6)
Use the formula M= y2-y1 ÷ x2-x1
Then m= 6-3 ÷ 4-2
Then m= 3÷2 = 1.5
So the slope should be 1.5 or 1 1/2