Answers
Answer:
D : 1/9^5
Step-by-step explanation:
you would first start off by subtracting the powers ( 7-2 ), which gives us 5. That then gives you 9^5, however, 9^5 gives you 59049, and the original problem's answer was 1/59049. When you divide 1 by 9^5, you get 1/59049, which is the same as the original answer.
Related Questions
There are 180 girls in a mixed school. if the ratio of girls to Boyd is 4:3,find the total number of students in the school.
Answers
Step 1) Set up a proportion
180 girls / x boys = 4 girls / 3 boys
540 = 4x
x = 135 boys
Step 2) Add the number of boys and girls together
180 + 135 = 315
Answer: 315 total students
the length of a rectangle is 4 times it’s width. The rectangle has an area of 1024cm squared
Answers
\(Your answer it W^2 = 1024/4 = 256.\)
Step-by-step explanation:

if f(x) = -3x - 5 and g(x) = 4x-2, find (f+g)(x)
Answers
Answer:
(f+g)(x) = x - 7
Step-by-step explanation:
it is simple - when adding 2 functions your simply add both expressions. and the result is then the function of the sum.
the same applies also to other arithmetic operations.
-3x -5 + 4x - 2 = x - 7
I need help with my math homework --WARNING--English is not my first language, sorry if I make spelling mistakes in my questions :(

Answers
Answer:
1. x = 4.5
2. x = 0.75 or x = -4.5
Explanation:
The quadratic formula says the solutions of the equation with the form ax² + bx + c are:
\(x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}\)So, if the equation is 4x² - 36x + 81, the value of each constant is
a = 4
b = -36
c = 81
Then, the solutions are
\(\begin{gathered} x=\frac{-(-36)\pm\sqrt[]{(-36)^2-4(4)(81)}}{2(4)} \\ x=\frac{36\pm\sqrt[]{1296-1296}}{8} \\ x=\frac{36\pm\sqrt[]{0}}{8}=\frac{36}{8}=4.5 \end{gathered}\)It means that this equation has a unique solution x = 4.5
In the same way, if we have the equation 8x² + 30x = 27, we first need to subtract 27 from both sides, so:
8x² + 30x - 27 = 27 - 27
8x² + 30x - 27 = 0
Now, we can identify the values of a, b, and c.
a = 8
b = 30
c = -27
Therefore, the solutions of the equation are
\(\begin{gathered} x=\frac{-30\pm\sqrt[]{(30^2)-4(8)(-27)}}{2(8)} \\ x=\frac{-30\pm\sqrt[]{900+864}_{}}{16} \\ x=\frac{-30\pm\sqrt[]{1764}}{16} \\ x=\frac{-30\pm42}{16} \\ \text{ The solutions are} \\ x=\frac{-30+42}{16}=\frac{12}{16}=0.75 \\ or \\ x=\frac{-30-42}{16}=\frac{-72}{16}=-4.5 \end{gathered}\)So, the solutions for each quadratic equation are:
1. x = 4.5
2. x = 0.75 or x = -4.5
The diagram shows a prism. Draw the front and side elevation of the prism on the grid. Use the scale 2 squares to 1m.
I know that the side elevation is correct but I can't get the front. Please help!

Answers
The sketch of the front elevation and the side elevation of the prism are added as an attachment
How to draw the front elevation and the side elevation of the prismFrom the question, we have the following parameters that can be used in our computation:
The prism
Using the figure as a guide, we understand that:
The front elevation is a rectangle of 2m by 0.5m
While the side elevation is a rectangle merged with a trapezoid
Next, we draw the elevations (see attachment)
Read more about prism at
brainly.com/question/23178481
#SPJ1

PLEASE HELPP!!!!!!!!!



Answers
The number of tickets that Sam can buy, given the amount he has to spend and the price of admission, is 36 tickets.
The rate of change is $ 0.75 per attraction.
The table on the number of tickets and total cost is:
Number of tickets 1 5 10 15
Total cost $ 10. 75 $ 13.75 $17.50 $ 21. 25
How to find the cost of tickets ?The number of tickets that Sam can buy when he has $ 37 is:
= (Amount to spend - Cost of admission ) / Cost per ticket
= ( 37 - 10 ) / 0.75
= 36 tickets
The rate of change is therefore the $ 0.75 charged per ticket per event.
The number of tickets for $ 10. 75 is:
= ( Total cost - Cost of admission ) / cost per ticket
= ( 10. 75 - 10 ) / 0.75
= 1 ticket
The cost of 5 tickets :
= ( Number of tickets x cost per ticket) + cost of admission
= (5 x 0. 75 ) + 10
= $ 13. 75
Find out more on total cost at https://brainly.com/question/22500858
#SPJ1
Find the distance between the two points rounding to the nearest tenth
(-4, 2) and (3, 5)
Answers
Answer:
-8.66666666666666666666666666666666666
-9
Step-by-step explanation:
Q.2 Solve the Initial-value problem
\( \frac{dy}{dx} = \frac{ {x}^{2} + x }{ \sqrt{x} } . \: y(1) = 0\)
Answers
The equation is separable:
\(\dfrac{\mathrm dy}{\mathrm dx}=\dfrac{x^2+x}{\sqrt x}\implies \mathrm dy=\left(x^{3/2}+x^{1/2}\right)\,\mathrm dx\)
Integrate both sides to get
\(y=\dfrac25x^{5/2}+\dfrac23x^{3/2}+C\)
Given that \(y(1)=0\), we find
\(0=\dfrac25+\dfrac23+C\implies C=-\dfrac{16}{15}\)
so the IVP has the solution
\(\boxed{y(x)=\dfrac25x^{5/2}+\dfrac23x^{3/2}-\dfrac{16}{15}}\)
Write the equation of a circle with a diameter endpoints of 13 and -1 and 15 and 9
Answers
The equation of a circle with diameter endpoints of (13, -1) and (15, 9) will be x² + y² - 28x - 8y + 186 = 0.
Given that:
Endpoints of diameter, (13, -1) and (15, 9)
The equation of the circle when endpoints of diameter are given is written as,
(x - x₁)(x - x₂) + (y - y₁)(y - y₂) = 0
The equation of the circle is calculated as,
(x - 13)(x - 15) + (y + 1)(y - 9) = 0
x² - 28x + 195 + y² - 8y - 9 = 0
x² + y² - 28x - 8y + 186 = 0
The equation of a circle with diameter endpoints of (13, -1) and (15, 9) will be x² + y² - 28x - 8y + 186 = 0.
More about the equation of the circle link is given below.
https://brainly.com/question/10618691
#SPJ1
82°
118°
95°
X°
Image not to scale
Calculate the missing angle x.

Answers
Answer:
x = 65
Step-by-step explanation:
the sum of the interior angles of a quadrilateral = 360°
sum the angles and equate to 360
x + 95 + 118 + 82 = 360
x + 295 = 360 ( subtract 295 from both sides )
x = 65
HELP PLEASE IM GIVE BRAINLIST

Answers
The triangle which could be drawn as per the given description is only option b. isosceles triangle with measure 20° and 80°.
An acute triangle with sides measuring 7, 4, and 2
In an acute triangle, the sum of the squares of the two shorter sides must be greater than the square of the longest side .
According to the Pythagorean Theorem.
Here, 7² is greater than (4² + 2²).
So this is not possible.
An isosceles triangle with angles measuring 20° and 80°
In an isosceles triangle, two angles are equal, so if two angle measures 20° and 80°,
Then the third angle measures is
180° - 20° - 80°= 80°
Two angles are congruent implies two sides are congruent.
It is possible to form isosceles triangle.
An obtuse triangle with sides measuring 5, 10, and 15
In an obtuse triangle, the longest side is opposite the largest angle.
Sum of squares of two shorter sides is less than square of longest side according to Pythagorean Theorem.
However, 15²is greater than (5²+ 10²),
so this is not possible.
A scalene triangle with angles measuring 110° and 35°
The sum of the angles of any triangle is 180°,
so the third angle must measure
180° - 110° - 35° = 35°.
Two angles are congruent so it is isosceles triangle.
It is not possible to form scalene triangle.
Therefore, the triangle possible to draw as per the given condition is only option b. isosceles triangle with measure 20° and 80°.
Learn more about triangle here
brainly.com/question/15833022
#SPJ1
Compare The Following
a) 169.188 ___ 169.098
Answers
Answer:
169.188 _\(\geq\)__ 169.098
Step-by-step explanation:
PLS HURRY FOR 80 POINTS Triangle XYZ is drawn with vertices X(4, −5), Y(6, −1), Z(10, −8). Determine the line of reflection if X′(4, 5).
y-axis
x-axis
y = 1
x = −4
Answers
Answer: a
Step-by-step explanation:
ILL GIVE BRAINLIESTTTT PLEASE HELP ILL GIVE BRAINLIESTTTT

Answers
Answer:
c) Propability of rolling doubles=6
Propability of rolling a sum grrater then or equal to 8 = 15
(Together add up to 21)
d)6 ->(1,1)(1,2)(1,3)(2,1)(2,2)(3,1)
e)9 ->(1,6)(3,4)(5,2)(3,5)(5,3)(3,6)(5,4)(5,5)(5,6)
The endpoints of a line are (10, 4) and (-2, 8). Find the slope of
the line.
Answers
write an equation in slope intercept form that passes through the given point and is perpendicular to the graph of given equation (1,-2) y=5x+4
Answers
The equation of the line perpendicular to y = 5x + 4, passing through the point (1, -2), is y = (-1/5)x - 9/5.
To find an equation in slope-intercept form that passes through the point (1, -2) and is perpendicular to the given equation y = 5x + 4, we need to determine the slope of the perpendicular line.
The given equation y = 5x + 4 is already in slope-intercept form (y = mx + b), where m represents the slope. In this case, the slope of the given line is 5.
To find the slope of a line perpendicular to this, we use the fact that the product of the slopes of two perpendicular lines is -1. So, the slope of the perpendicular line can be found by taking the negative reciprocal of the slope of the given line.
The negative reciprocal of 5 is -1/5.
Now that we have the slope (-1/5) and a point (1, -2), we can use the point-slope form of the equation:
y - y1 = m(x - x1)
Substituting the values:
y - (-2) = (-1/5)(x - 1)
Simplifying:
y + 2 = (-1/5)(x - 1)
To convert the equation into slope-intercept form (y = mx + b), we need to simplify it further:
y + 2 = (-1/5)x + 1/5
Subtracting 2 from both sides:
y = (-1/5)x + 1/5 - 2
Combining the constants:
y = (-1/5)x - 9/5
Therefore, the equation of the line perpendicular to y = 5x + 4, passing through the point (1, -2), is y = (-1/5)x - 9/5.
For more question on perpendicular visit:
https://brainly.com/question/1202004
#SPJ8
An ectopic pregnancy is twice as likely to develop when the pregnant woman is a smoker as it iswhen she is a nonsmoker. If 32 percent of women of childbearing age are smokers, what percentageof women having ectopic pregnancies are smokers?
Answers
Answer:
48.48%
Step-by-step explanation:
Let's assume that there is a number N of women.
32% of these are smokers, then there are 0.32*N smokers
then 68% of these are non-smokers, then there are 0.68*N non-smokers.
Let's assume that the probability of having a ectopic pregnancy for a non-smoker is p (and the probability for a smoker will be 2*p)
Then the number of women with an ectopic pregnancy that are non-smokers is:
p*0.68*N
The number of women with an ectopic pregnancy that are smokers is:
2*p*0.32*N
Then the total number of women with an ectopic pregnancy will be:
p*0.68*N + 2*p*0.32*N
The percentage of women having an ectopic pregnancy that are smokers is equal to the quotient between the number of women with an ectopic pregnancy that are smokers and the total number of women with an ectopic pregnancy, all that times 100%.
The percentage is:
\(P = \frac{2*p*0.32*N}{p*0.68*N + 2*p*0.32*N} *100\%\)
Taking p and N as common factors, we get:
\(P = \frac{2*p*0.32*N}{p*0.68*N + 2*p*0.32*N} *100\% = \frac{N*p}{N*p} \frac{2*0.32}{0.68 + 2*0.32} *100\%\)
Then we get:
\(\frac{2*0.32}{0.68 + 2*0.32} *100\% = 48.48\%\)
Evaluate the expression (image provided). A.) 1.5 B.) 6 C.) 6^15 D.) 1.5^6

Answers
Answer:
1.5
Step-by-step explanation:
6 to the log base of 6 will be one (they essentially cancel each other out, log is the opposite of exponents) and we are left with 1.5.
4(2n-5)=3n+10
n=??????
Answers
Answer:
n = 6
Step-by-step explanation:
Distribute 4 in 2n - 5:
\(\displaystyle{4\cdot 2n - 4\cdot 5 = 3n + 10}\\\\\displaystyle{8n-20=3n+10}\)
Subtract both sides by 3n:
\(\displaystyle{8n-20-3n=3n+10-3n}\\\\\displaystyle{5n-20=10}\)
Add both sides by 20:
\(\displaystyle{5n-20+20=10+20}\\\\\displaystyle{5n=30}\)
Divide both sides by 5:
\(\displaystyle{\dfrac{5n}{5}=\dfrac{30}{5}}\\\\\displaystyle{n=6}\)
Therefore, n = 6
Answer:
n=6
Step-by-step explanation:
Original equation: 4(2n-5)=3n+10
Step 1 (Distribute the 4):
4(2n)-4(5)=3n+10
8n-20=3n+10
Step 2 (Subtract 3n from both sides):
8n-20-3n=3n+10-3n
(8n-3n)-20=(3n-3n)+10
5n-20=10
Step 3 (Add 20 to both sides):
5n-20+20=10+20
5n=30
Step 4 (Divide both sides by 5):
5n/5=30/5
n=6
Holly buys a $22 shirt for 20% off. The tax rate in her city is 6.5%. What is the total amount she paid for the shirt? Round to the nearest cent.
A.$2
B.$18.74
C.$24.10
D.$8.50
Answers
The total amount Holla paid for the shirt is: B. $18.74
Given the following data:
Cost of shirt = $22Discount = 20% Tax rate = 6.5%To find the total amount she paid for the shirt:
First of all, we would determine the discount on the shirt:
\(Discount = \frac{20}{100} \times 22\\\\Discount = 0.2 \times 22\)
Discount cost = $4.4
\(Selling\; price = Cost\;price - Discount \\\\Selling\; price = 22 - 4.4\)
Selling price = $17.6
Next, we would determine how much tax is to be paid:
\(Tax \;cost = \frac{6.5}{100} \times 17.6\\\\Tax \;cost = 0.065 \times 17.6\)
Tax cost = $1.444
\(Total\;amount = selling \;price + tax\;cost\\\\Total\;amount = 17.6 + 1.444\)
Total amount = $18.74
Read more: https://brainly.com/question/13282374
Two bells P and Q ring at intervals of 3hours and 4hours respectively. After how many hours will the two bells first ring simultaneously (at the same time)
Answers
Answer:
12 hours
Step-by-step explanation:
4 / 2
2/2
1
4 = 2²
2² x 3 = 4 x 3 = 12
How would I do this

Answers
Answer:
the ramp must be lowered
Step-by-step explanation:
Use the definition of the sine function to find the height of a ramp that is 8°.
Sine = Opposite/Hypotenuse
sin(8°) = height/8
height = 8×sin(8°) = 1.11
The height Nate's dad allows is 1.11 feet. At 1.5 feet, the ramp is too high.
The ramp must be lowered.
SOMEBODY HELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIEST
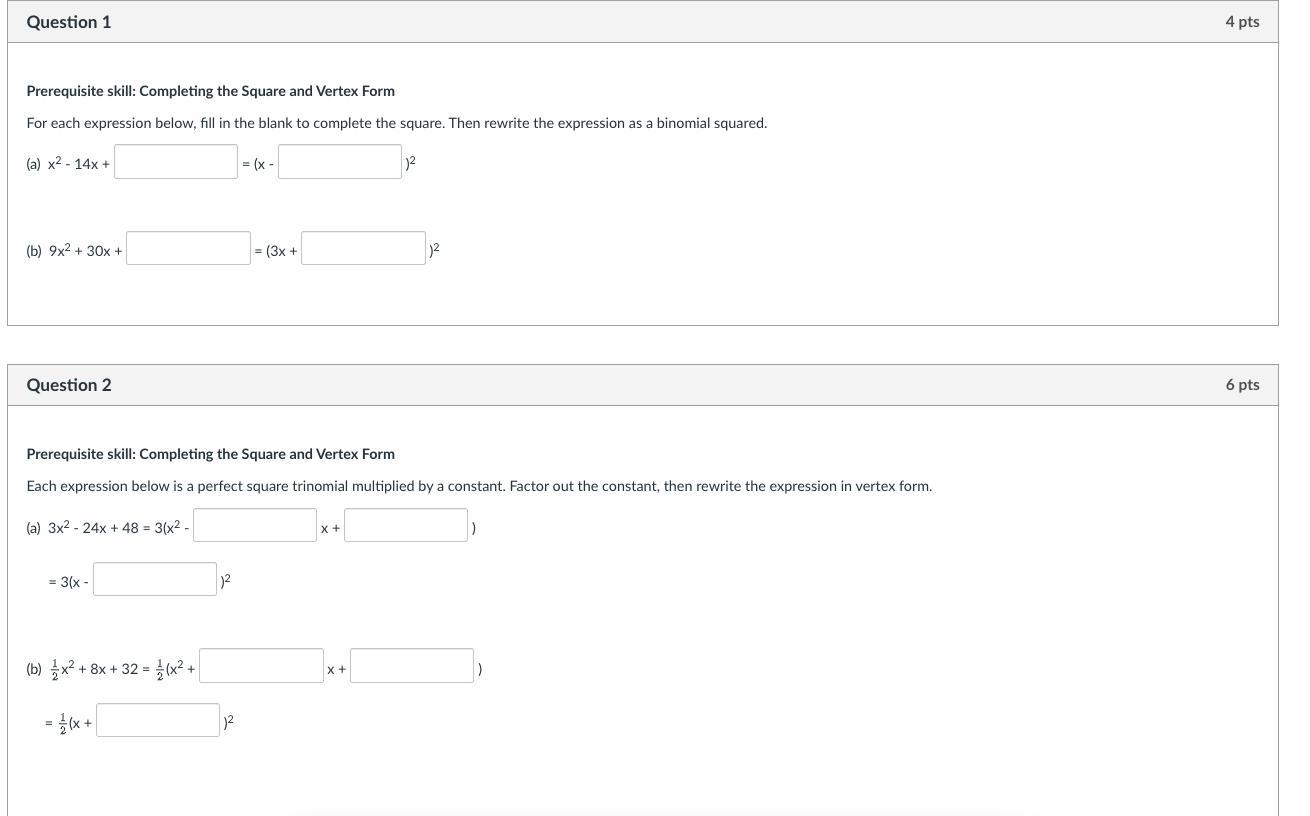
Answers
Answer:
\(\textsf{1.(a)} \quad x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
\(\textsf{1.(b)} \quad 9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\begin{aligned}\textsf{2.(a)}\quad3x^2-24x+48&=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\\&=3\left(x-\boxed{4}\right)^2\end{aligned}\)
\(\begin{aligned}\textsf{2.(b)}\quad \dfrac{1}{2}x^2+8x+32&=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\\&=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\end{aligned}\)
Step-by-step explanation:
Question 1(a) When completing the square for a quadratic equation in the form ax² + bx + c where the leading coefficient is one, we need to add the square of half the coefficient of the x-term:
\(x^2-14x+\left(\dfrac{-14}{2}\right)^2\)
\(x^2-14x+\left(-7\right)^2\)
\(x^2-14x+49\)
We have now created a perfect square trinomial in the form a² - 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Therefore:
\(a^2=x^2 \implies a=1\)
\(b^2=49=7^2\implies b = 7\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
(b) When completing the square for a quadratic equation where the leading coefficient is not one, we need to add the square of the coefficient of the x-term once it is halved and divided by the leading coefficient, and then multiply it by the leading coefficient:
\(9x^2 + 30x +9\left(\dfrac{30}{2 \cdot 9}\right)^2\)
\(9x^2 + 30x +9\left(\dfrac{5}{3}\right)^2\)
\(9x^2 + 30x +9 \cdot \dfrac{25}{9}\)
\(9x^2 + 30x +25\)
We have now created a perfect square trinomial in the form a² + 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 +2ab + b^2 = (a +b)^2}\)
Therefore:
\(a^2=9x^2 = (3x)^2 \implies a = 3x\)
\(b^2=25 = 5^2 \implies b = 5\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\hrulefill\)
Question 2(a) Factor out the leading coefficient 3 from the given expression:
\(3x^2-24x+48=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\)
We have now created a perfect square trinomial in the form a² - 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=3\left(x-\boxed{4}\right)^2\)
(a) Factor out the leading coefficient 1/2 from the given expression:
\(\dfrac{1}{2}x^2+8x+32=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\)
We have now created a perfect square trinomial in the form a² + 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2+2ab + b^2 = (a +b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\)
Step-by-step explanation:
Since ABCD is a rectangle
⇒ AB = CD and BC = AD
x + y = 30 …………….. (i)
x – y = 14 ……………. (ii)
(i) + (ii) ⇒ 2x = 44
⇒ x = 22
Plug in x = 22 in (i)
⇒ 22 + y = 30
⇒ y = 8
HELP!!
You use a line of best fit for a set of data to make a prediction about an unknown value. The correlation coefficient for your data set is 0.214. How confident can you be that your predicted value will be reasonably close to the actual value?
Answer Choices Below!:

Answers
Answer:
A
Step-by-step explanation:
The lines shown below are perpendicular. If the green line has a slope of 2,
what is the slope of the red line?
-10
10
16
A. ¾/1
O A.
B.
O C.
O D. - 3/4
Answers
None of the given answer options (-10, 10, 16, ¾/1) correspond to the correct slope of -1/2.
To find the slope of the red line given that it is perpendicular to the green line with a slope of 2, we can use the property that perpendicular lines have slopes that are negative reciprocals of each other.
The slope of the green line is 2. To find the slope of the red line, we take the negative reciprocal of 2. The negative reciprocal is obtained by taking the reciprocal (flipping the fraction) and changing the sign.
Reciprocal of 2: 1/2
Negative reciprocal: -1/2
Therefore, the slope of the red line is -1/2.
However, none of the given answer options (-10, 10, 16, ¾/1) correspond to the correct slope of -1/2.
for such more question on perpendicular
https://brainly.com/question/18991632
#SPJ8
If each of these runners travels the indicated number of spaces in the same amount of time, at which numbered spot will all of the runners be next to one another?

Answers
The numbered spot at which all the runners will be next to one another is spot 19.
What is the LCM?Least Common Multiple is the meaning of the acronym LCM. The lowest number that may be divided by both numbers is known as the least common multiple (LCM) of two numbers. It may also be computed using two or more real numbers.
Starting with the runner on the outside track, the provided parameters are;
The runner covered n₁ = 5 places on the outside track, which is the number of spaces.
Next, the inner runner will traverse n₂ spaces, which equals one space.
The following inner runner will cover n₃ = 3 spaces.
The subsequent runner will traverse n₄ = 2 spaces.
The Lowest Common Multiple, or LCM, of all the runners' speeds or the total number of spaces they cover in the same amount of time, determines where all the runners will be placed next to one another.
LCM(5, 1, 3, 2) = 30 is the LCM of 5, 1, 3, and 2.
Time = 30/ = 6
Consequently, when the first runner has covered 30 places, we have;
Six time units have been expended.
The runner comes to a stop at position 30- (30 -19) = Position 19.
First runner's new destination is Spot 19.
The distance covered simultaneously by runner 2 is 6 x 1 = 6.
The distance covered by two runners running simultaneously equals six spaces.
Second runner's new position: 6 spaces plus spot 13 equals spot 19.
The combined distance covered by the three runners is 6 x 3 = 18.
The distance runner 3 covers 18 spaces simultaneously.
Third runner's new position: 18 spaces + Spot 1 = 19 spaces
Runner 4 covers a distance of 6 x 2 = 12 at the same time.
Distance runner 4 journeys equals 12 spaces
Runner 4's new position is now 12 spaces Plus Spot 7 = Spot 19.
Therefore, all the runners will be next to one another is spot 19.
To learn more about the LCM;
https://brainly.com/question/20739723
#SPJ1
find the cartesian equation of r=3i+paremeter (i+2j)
Answers
The Cartesian equation will be;
⇒ (x - 3) / 1 = (y - 0)/2
What is Equation of line?
The equation of line in point-slope form passing through the points (x₁ , y₁) and (x₂, y₂) with slope m is defined as;
⇒ y - y₁ = m (x - x₁)
Where, m = (y₂ - y₁) / (x₂ - x₁)
Given that;
The equation is,
⇒ r = 3i + λ (i + 2j)
Where, 'λ' is a parameter.
Now,
Since, The equation is,
⇒ r = 3i + λ (i + 2j)
Where, 'λ' is a parameter.
Hence, The Cartesian equation is find as;
⇒ xi + yj = 3i + λi + 2λj
By compare, we get;
⇒ x = 3 + λ
⇒ y = 2λ
Thus, The Cartesian equation is;
⇒ (x - 3) / 1 = (y - 0)/2 = λ
Therefore, The Cartesian equation will be;
⇒ (x - 3) / 1 = (y - 0)/2
Learn more about the Cartesian equation visit:
https://brainly.com/question/14869452
#SPJ1
3 Jack walk from Santa Clara to Polo Allo. Il took I hour 25 min to walk from Santa Clot to Los Altos. Than it took 25 minute of wal from los altos to Palo buto. He arrived in Palo alto at 2:45 P.M. of what time die Santa Clara ? he leave Santa clara
Answers
The time Jack left Santa Clara is 1 : 55 pm
What is word problem?A word problem in math is a math question written as one sentence or more. These statements are interpreted into mathematical equation or expression.
The time for Jack to walk to lose Altos is 25 min and he uses another 25mins to work to Palo alto.
Therefore, the total time he spent is
25mins + 25 mins = 50 mins
He arrived Palo at 2 :45 pm, therefore the time he left Santa Clare will be ;
2:45 pm = 14 :45
= 14:45 - 50mins
= 13:55
= 1 : 55pm
Therefore he left at 1:55 pm
learn more about word problem from
https://brainly.com/question/21405634
#SPJ1
Justin is on a road trip. Over the past 2 days, he has driven a total distance of 715 miles at an average speed of 65 miles per hour. If
Justin drove 2 hours today, how many hours did he drive yesterday?
Answers
Answer:
1 hour did he drive yesterday
After graduating from college, Trevor gets a job at a software company with a starting salary of 50,000 dollars and is given a 10% raise every year. After 10 years, what will his total earnings have been at the company? (Round to the nearest dollar)
Answers
Answer:
796871
Step-by-step explanation:
Based on the given conditions, formulate:
5000 x (1 - (1 + 10%) 10)
-------------------------------
1 - (1 + 10%)
Evaluate the equation/expression:
796871.23005
Find the closest integer to
798871.23005
= 796871
